Với tóm tắt lý thuyết Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản

Video giải Toán 6 Chương 8: Hình học phẳng và các hình học cơ bản – Chân trời sáng tạo

A. Lý thuyết Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản

1. Điểm

Mỗi chấm nhỏ trên trang giấy, trên bảng, … cho ta hình ảnh của một điểm.

Người ta thường dùng các chữ cái in hoa A, B, C, D, …. để đặt tên cho điểm.

Chú ý: 

- Khi nói tới hai điểm mà không giải thích gì thêm, ta coi đó là hai điểm phân biệt.

- Từ những điểm, ta xây dựng được các hình. Mỗi hình là một tập hợp các điểm. Một điểm cũng được coi là một hình.

2. Đường thẳng

Dùng bút kẻ một vạch thẳng dọc theo mép thước ta sẽ được hình ảnh của một đường thẳng.

Chú ý: Ta thường dùng các chữ cái in hoa a, b, c, d, …. để đặt tên các đường thẳng.

3. Vẽ đường thẳng

Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

4. Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng

- Vẽ một điểm A trên giấy, dùng thước thẳng vẽ đường thẳng d đi qua điểm A. Khi đó, ta nói điểm A thuộc đường thẳng d (hoặc đường thẳng d chứa điểm A), hoặc điểm A nằm trên đường thẳng d), kí hiệu là: A∈d (như hình vẽ).

- Dùng thước thẳng vẽ đường thẳng d không đi qua điểm B.

Khi đó, ta nói điểm B không thuộc đường thẳng d (hoặc đường thẳng d không chứa điểm B hoặc điểm B không nằm trên đường thẳng d), kí hiệu là: B∉ d(như hình vẽ).

Chú ý: Nếu trên đường thẳng a có hai điểm A và B, ta cũng có thể gọi tên đường thẳng đó là đường thẳng AB hay BA (như hình vẽ).

5. Ba điểm thẳng hàng

- Ba điểm phân biệt A, B, C cùng thuộc một đường thẳng được gọi là ba điểm thẳng hàng.

Ta có hình vẽ:

- Ba điểm D, E, F không cùng thuộc bất kì một đường thẳng nào được gọi là ba điểm không thẳng hàng.

Ta có hình vẽ:

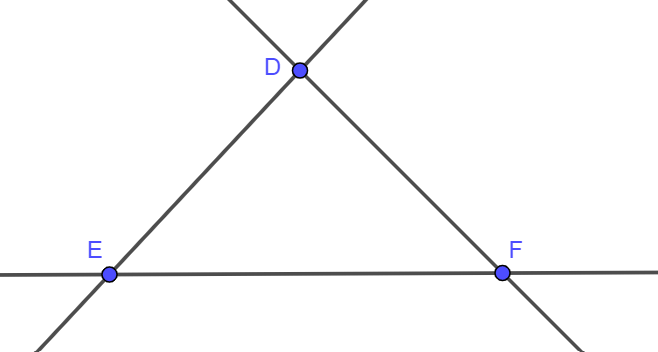
6. Quan hệ giữa ba điểm thẳng hàng

Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.

Chẳng han: Với ba điểm A, B, C thẳng hàng. Điểm B nằm giữa hai điểm còn lại (như hình vẽ).

Trong hình vẽ trên:

- Các điểm B và C nằm cùng phía đối điểm A;

- Các điểm A và C nằm khác phía đối với điểm B.

7. Hai đường thẳng cắt nhau, song song

- Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.

Chú ý: Từ nay về sau, khi nói hai đường thẳng mà không nói gì thêm, ta hiểu đó là hai đường thẳng phân biệt.

8. Tia

Mỗi điểm O trên một đường thẳng chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc O.

Chú ý:

- Từ một điểm O kẻ một vạch thẳng về một phía của điểm O để biểu diễn một tia gốc O.

- Nếu A là một điểm tùy ý trên tia Ox, ta có thể gọi tia Ox là tia OA (như hình vẽ).

- Khi viết (đọc) tia, ta phải viết (đọc) gốc của tia trước.

9. Đoạn thẳng

Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa A và B.

Đoạn thẳng AB còn gọi là đoạn thẳng BA.

Hai điểm A, B gọi là hai đầu mút (hoặc hai đầu) của đoạn thẳng AB.

Ta có hình vẽ:

10. Độ dài đoạn thẳng

Cách đo độ dài đoạn thẳng AB:

Cho đoạn thẳng AB. Đặt cạnh của thước đi qua hai điểm A và B sao cho điểm A trùng với vạch số 0 của thước và nhìn xem điểm B trùng với vạch chỉ số bao nhiêu.

Giả sử điểm B trùng với vạch số 9 (như hình vẽ).

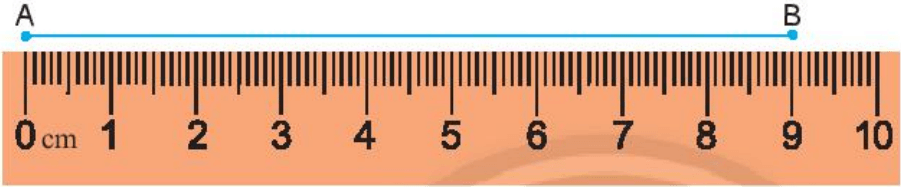
Khi đó, ta nói đoạn thẳng AB có độ dài là 9 cm. 

Kí hiệu AB = 9 cm hoặc BA = 9 cm.

Việc đo độ dài đoạn thẳng được thực hiện trên cơ sở so sánh nó với đoạn thẳng được chọn làm đơn vị đo hay đoạn thẳng đơn vị. 

Nhận xét:

- Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương.

- Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B.

- Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng 0.

Số đo độ dài của một đoạn thẳng không phải bao giờ cũng là số tự nhiên. 

11. So sánh hai đoạn thẳng

Ta so sánh hai đoạn thẳng bằng cách so sánh độ dài của chúng.

Chẳng hạn:

- Đoạn thẳng AB bằng đoạn thẳng CD và viết là AB = CD. 

- Đoạn thẳng EF dài hơn đoạn thẳng AB và viết là EF > AB.

- Đoạn thẳng CD ngắn hơn đoạn thẳng EF và viết là CD < EF.

12. Trung điểm của đoạn thẳng

Trung điểm của đoạn thẳng là điểm nằm giữa hai đầu mút của đoạn thẳng và cách đều hai đầu mút đó. Trung điểm của đoạn thẳng còn được gọi là điểm chính giữa của đoạn thẳng đó.

13. Cách vẽ trung điểm của đoạn thẳng

Giả sử ta cần vẽ trung điểm M của đoạn thẳng AB có độ dài 5 cm.

Cách 1:

- Đặt mép thước trùng với đoạn thẳng AB sao cho vạch 0 trùng với điểm A, khi đó điểm B trùng với vạch chỉ số 5 trên thước.

- Ta lấy điểm M trùng với vạch chỉ số 2,5 cm trên thước. Khi đó ta có M là trung điểm của đoạn thẳng AB (như hình vẽ).

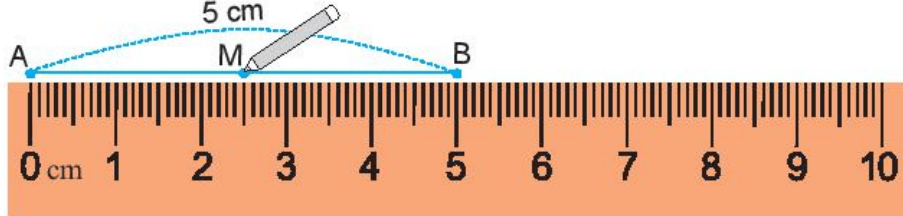
Cách 2: 

Vẽ đoạn thẳng AB trên giấy can sao cho điểm B trùng với điểm A. Giao của nếp gấp và đoạn thẳng AB chính là trung điểm M cần xác định.

14. Góc

Góc là hình tạo bởi hai tia chung gốc. 

Gốc chung của hai tia gọi là đỉnh của góc, hai tia gọi là hai cạnh của góc.

Kí hiệu: Góc xAy kí hiệu là  .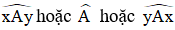

Chú ý: Trên hình vẽ, trong trường hợp nhiều góc có chung một đỉnh, người ta thường khoanh một cung giữa hai cạnh và đánh số: 1, 2, 3, … hoặc mỗi góc có khoanh những cung khác nhau chỉ các góc khác nhau đó.

15. Cách vẽ góc 

Để vẽ 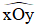, ta vẽ điểm O trên giấy hoặc bảng, từ điểm O vẽ hai tia Ox và Oy.

Ta có hình vẽ:

16. Góc bẹt 

Góc bẹt là hai cạnh của góc cùng nằm trên một đường thẳng.

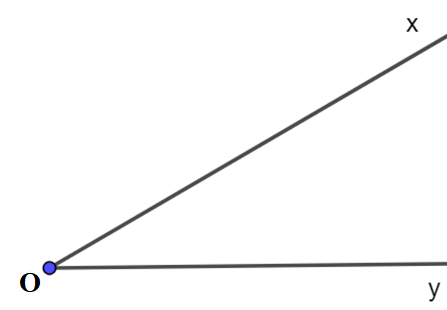
17. Điểm trong của góc

Cho góc xOy khác góc bẹt. Điểm M được gọi là điểm trong của góc xOy không bẹt nếu tia OM cắt một đoạn thẳng nối hai điểm trên hai cạnh tại một điểm nằm giữa hai điểm đó.

Ta có hình vẽ điểm M là điểm trong của góc xOy không bẹt.

18. Thước đo góc

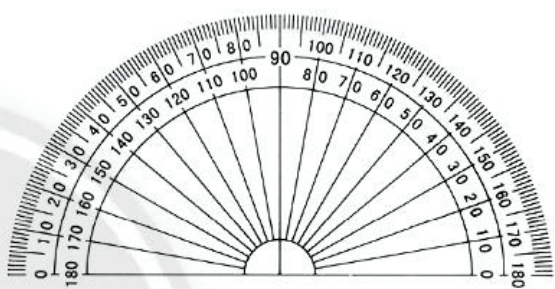
Trong hình vẽ trên là thước đo góc được dùng để đo hoặc vẽ góc. Thước có dạng một nửa hình tròn và được chia thành 180 phần bằng nhau bởi các vạch được ghi từ 0 đến 180. Mỗi một phần của thước ứng với 1 độ. Dấu ^o thay cho chữ “độ”.

Độ là đơn vị đo góc.

Ta gọi tâm của nửa hình tròn này là tâm của thước.

 19. Cách đo góc. Số đo góc

- Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

- Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc (như hình vẽ).

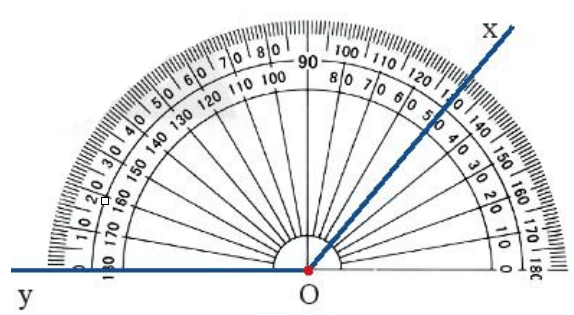
- Bước 3: Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.

Chẳng hạn: trong hình vẽ trên, tia Ox đi qua vạch chỉ số 130 của thước đo góc.

Do đó, số đo góc xOy là 130^o.

Nhận xét:

- Mỗi góc có một số đo. Số đo của góc bẹt là 180^o.

- Số đo của mỗi góc không vượt quá 180^o.

Chú ý:

- Trên thước đo góc, người ta ghi các số từ 0 đến 180 ở hai vòng cung theo hai chiều ngược nhau để việc đo góc được thuận tiện. Nếu một cạnh của góc trùng với cạnh ở nửa bên phải của thước đo thì chúng ta sử dụng thang ở bên trong, nếu nửa bên trái thì chúng ta sử dụng thang bên ngoài.

20. So sánh hai góc

Giả sử, 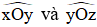 bằng nhau, kí hiệu là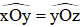 

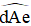 lớn hơn , kí hiệu là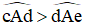 

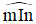 nhỏ hơn 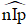, kí hiệu là .

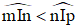21. Các góc đặc biệt 

- Góc có số đo bằng 90^o là góc vuông.

- Góc có số đo nhỏ hơn 90^o là góc nhọn.

- Góc có số đo lớn hơn 90^o là góc tù.

B. Bài tập tự luyện 

Bài 1. 

a) Hãy đặt tên cho các điểm và đường thẳng trong hình dưới đây.

 

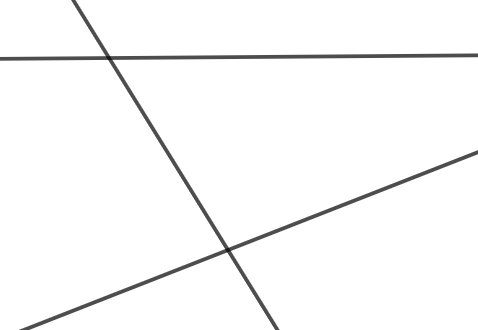
b) Hãy nêu ba cách gọi tên đường thẳng trong hình dưới đây.

Lời giải:

a) Đường thẳng được đặt tên bởi chữ in thường như: a, b, c, x, y, …

Điểm được đặt tên bởi chữ in hoa: A, B, C, D, …

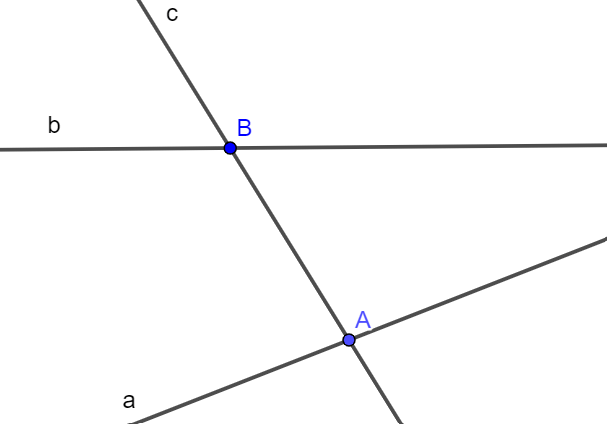
Chẳng hạn: ta đặt tên các điểm là A, B và các đường thẳng là a, b, c (như hình vẽ).

 

b) Ta có thể gọi tên đường thẳng bằng cách:

- Gọi theo tên đường thẳng, thường được đặt bằng chữ cái thường a, b, c, …

- Gọi tên bằng hai điểm thuộc đường thẳng.

Ba cách gọi tên đường thẳng trong hình trên là: đường thẳng AB, đường thẳng BC và đường thẳng AC.

Bài 2. Dùng kí hiệu để biểu thị các mối quan hệ dưới đây và vẽ các hình tương ứng.

a) Các điểm M, N thuộc đường thẳng a.

b) Các điểm P, Q không thuộc đường thẳng b.

Lời giải: 

a) Điểm thuộc đường thẳng ta dùng kí hiệu: ∈.

- Điểm A thuộc đường thẳng p. Ký hiệu: M∈a.

- Điểm B thuộc đường thẳng. Ký hiệu: N∈a.

Ta có hình vẽ:

b) Điểm không thuộc đường thẳng ta dùng kí hiệu: ∉.

- Điểm C không thuộc đường thẳng b. Ký hiệu: P∉ b.

- Điểm D không thuộc đường thẳng b. Ký hiệu: Q∉ b.

Ta có hình vẽ:

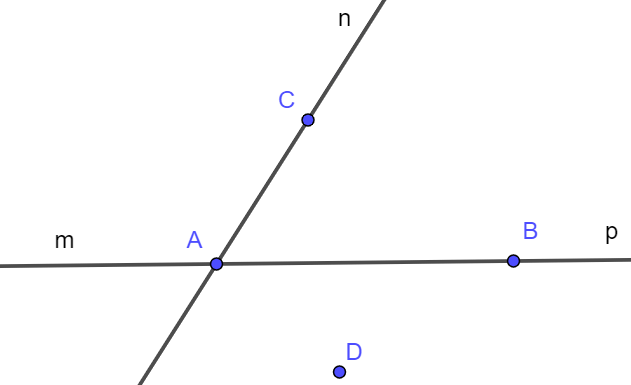
Bài 3. Trong hình vẽ bên:

a) Điểm A thuộc những đường thẳng nào?

b) Điểm B thuộc đường thẳng nào và không thuộc những đường thẳng nào?

c) Đường thẳng nào chứa điểm C?

d) Đường thẳng nào không chứa điểm D?

Sử dụng kí hiệu để mô tả các quan hệ trên.

Lời giải: 

a) Điểm thuộc đường thẳng ta dùng kí hiệu: ∈.

Trong hình vẽ trên, điểm A thuộc các đường thẳng: m, n và p. 

Ký hiệu: A∈ m, A∈ n, A∈ p.

b) Điểm không thuộc đường thẳng ta dùng kí hiệu: ∉.

Trong hình vẽ trên, điểm B thuộc đường thẳng p. Ký hiệu: B∈ p.

Điểm B không thuộc đường thẳng m và n.

Ký hiệu: B∉ m, B∉ n.

c) Trong hình vẽ trên, đường thẳng chứa điểm C là m và p. Hay điểm C thuộc hai đường thẳng m và p.

Ký hiệu: C∈ m, C∈ p.

d) Đường thẳng nào không chứa điểm D là m, n và p. Hay điểm D không thuộc đường thẳng m, n và p.

Kí hiệu: D∉ m, D∉ n, D∉ p.

Bài 4. Cho hình vẽ sau. Hãy nêu các bộ ba điểm thẳng hàng và bộ ba điểm không thẳng hàng.

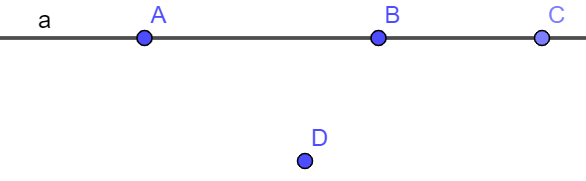
Lời giải: 

Trong hình vẽ trên, ba điểm A, B, C đều thuộc đường thẳng a và điểm D không thuộc đường thẳng a.

Vậy bộ ba điểm thẳng hàng: (A, B, C);

Các bộ ba điểm không thẳng hàng: (A, B, D); (A, C, D); (B, C, D).

Bài 5. Cho hai điểm E và F. Vẽ hình theo các diễn đạt sau:

a) Lấy điểm G sao cho ba điểm E, F, G thẳng hàng và E, F nằm cùng phía đối với điểm G.

b) Lấy điểm H sao cho ba điểm E, F, H thẳng hàng và E, F nằm khác phía đối với điểm H.

Lời giải:

- Lấy hai điểm điểm E, F bất kỳ (hai điểm E và F phân biệt).

- Vẽ đường thẳng đi qua hai điểm E và F. 

Ta có đường thẳng EF (như hình vẽ).

a) Trên đường thẳng EF lấy điểm G sao cho hai điểm E và F nằm cùng phía đối với điểm G. Ta có hai trường hợp sau:

- Trường hợp 1: Điểm G nằm bên trái điểm E (như hình vẽ).

- Trường hợp 2: Điểm G nằm bên phải điểm F (như hình vẽ).

b) Trên đường thẳng EF lấy điểm H sao cho hai điểm E và F nằm khác phía đối với điểm H. Hay điểm H nằm giữa hai điểm E và F.

Bài 6. Cho hình bình hành MNPQ. Hãy xác định điểm O sao cho các bộ ba điểm M, I, P và N, I, Q đều là các bộ ba điểm thẳng hàng.

Lời giải:

Ba điểm M, I, P thẳng hàng nên I thuộc đường thẳng MP. 

Ba điểm N, I, Q thẳng hàng nên I thuộc đường thẳng NQ. 

Do đó I là giao điểm của đường thẳng MP và đường thẳng NQ.

Điểm I thỏa mãn điều kiện các bộ ba điểm M, I, P và N, I, Q đều là các bộ ba điểm thẳng hàng có thể xác định như hình vẽ sau.

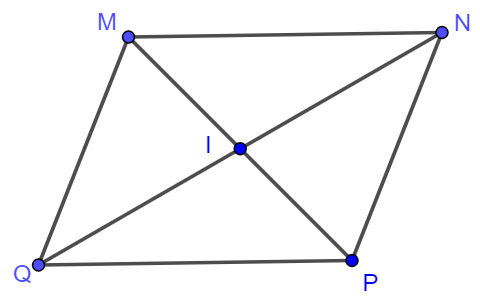
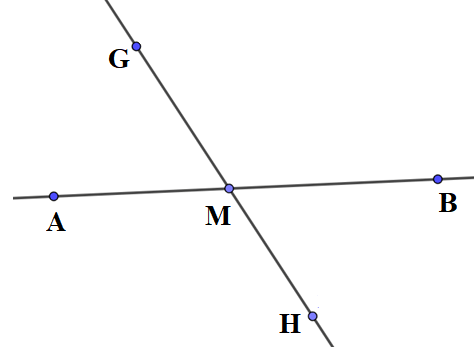
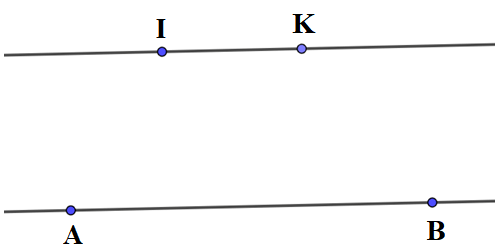
Bài 7. Cho đường thẳng AB bất kỳ. Hãy vẽ hình trong các trường hợp sau:

a) Đường thẳng GH cắt đường thẳng AB;

b) Đường thẳng IK song song với đường thẳng AB.

Lời giải: 

a) Đường thẳng GH cắt đường thẳng AB nên hai đường thẳng này có một điểm chung.  

Chẳng hạn: vẽ hai đường thẳng GH và AB cắt nhau tại điểm M.

Cách vẽ:

Bước 1: Vẽ đường thẳng AB bất kỳ.

Bước 2: Lấy điểm M bất kỳ thuộc đường thẳng AB, giả sử điểm M nằm giữa hai điểm A và B.

Bước 3: Vẽ đường thẳng đi qua M và không trùng với đường thẳng AB.

Ta có đường thẳng GH cắt đường thẳng AB như hình vẽ:

b) Cách vẽ đường thẳng IK song song với đường thẳng AB:

Bước 1: Vẽ đường thẳng AB bất kỳ.

Bước 2: Lấy điểm I nằm ngoài đường thẳng AB. 

Bước 3: Vẽ đường thẳng đi qua điểm I và song song với đường thẳng AB. Lấy điểm K thuộc đường thẳng vừa vẽ. 

Ta được đường thẳng IK song song với đường thẳng AB như hình vẽ:

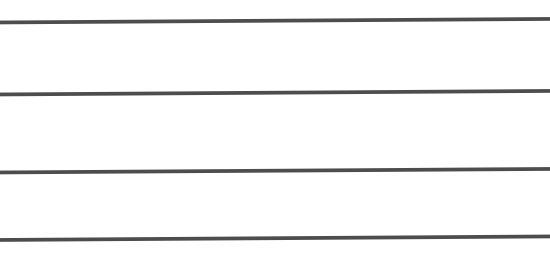
Bài 8. Đếm số giao điểm tạo bởi bốn đường thẳng trong mỗi hình sau:

a)

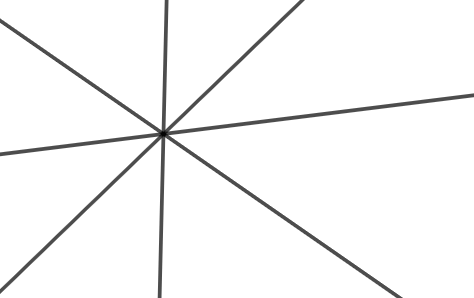
b)

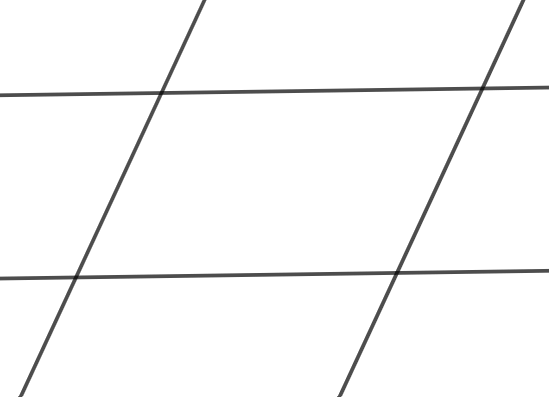
c) 

Lời giải: 

a) Trong hình a) có ba đường thẳng song song với nhau nên không có giao điểm nào.

b) Đặt các đường thẳng trong hình b) là các đường thẳng a, b, c, d.

Giả sử bốn đường thẳng a, b, c, d cắt nhau tại điểm M (như hình vẽ).

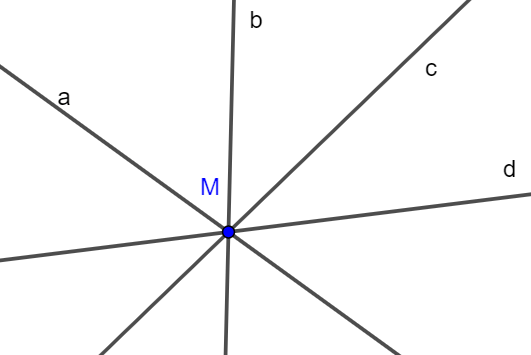
Vậy trong hình b) có một giao điểm tạo bởi bốn đường thẳng.

c) Đặt các đường thẳng trong hình c) là các đường thẳng m, n, p, q.

Giả sử đường thẳng m và p cắt nhau tại điểm A, đường thẳng n và p cắt nhau tại điểm B, đường thẳng m và q cắt nhau tại C, đường thẳng n và q cắt nhau tại D (như hình vẽ).

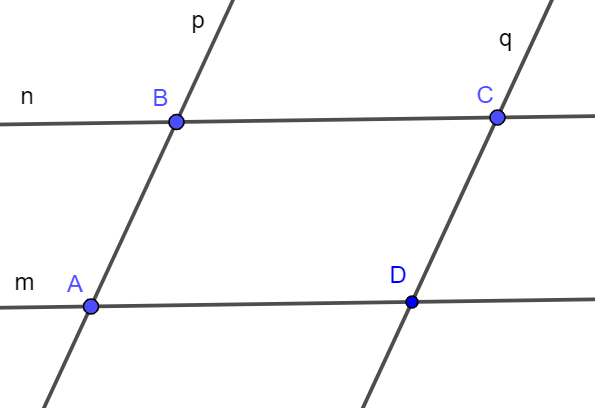
Do đó bốn đường thẳng m, n, p, q đôi một cắt nhau tại các điểm A, B, C, D.

Vậy trong hình c) có bốn giao điểm tạo bởi bốn đường thẳng.

Bài 9. Cho hai đường thẳng XY và EF cắt nhau tại điểm O. Kể tên các tia có gốc O.

Lời giải: 

Cách vẽ:

- Vẽ đường thẳng XY bất kỳ.

- Lấy điểm O thuộc đường thẳng XY.

- Vẽ đường thẳng EF đi qua O (đường thẳng EF không trùng với đường thẳng XY).

Ta có hình vẽ:

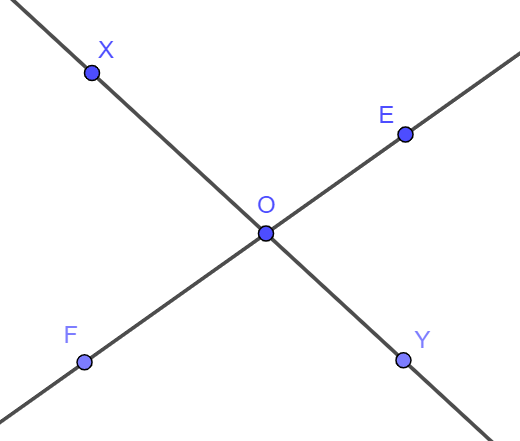
Hai đường thẳng XY và EF cắt nhau tại điểm O nên điểm O nằm trên hai đường thẳng này.

- Điểm O nằm trên đường thẳng XY nên điểm O chia đường thẳng XY thành hai tia có chung gốc O là tia OX, OY.

- Điểm O nằm trên đường thẳng EF nên điểm O chia đường thẳng EF thành hai tia có chung gốc O là tia OE, OF.

Vậy các tia có gốc O là: OX, OY, OE, OF.

Bài 10. Kể tên các đoạn thẳng có trong hình dưới đây:

Lời giải: 

Cứ hai điểm bất kỳ được nối với nhau sẽ tạo thành một đoạn thẳng.

Ta có các cách chọn sau: (A, B); (A, C); (A, D); (B, C); (B, D); (C, D). 

Trong mỗi cách chọn, cứ hai điểm sẽ tạo thành một đoạn thẳng.

Vậy các đoạn thẳng có trong hình trên là: AB, AC, AD, BC, BD, CD.

Bài 11. Cho hai điểm M và N cách nhau một khoảng bằng 9 cm. Nếu ta chọn một đoạn thẳng có độ dài 3 cm làm đơn vị độ dài thì đoạn MN có độ dài bằng bao nhiêu đơn vị vừa chọn?

Lời giải:

Hai điểm M và N cách nhau một khoảng bằng 9 cm hay độ dài đoạn thẳng MN = 9 cm.

Gọi đoạn thẳng đơn vị có độ dài 3 cm là đoạn thẳng AB. 

Khi đó, AB = 3 cm.

Ta có hình vẽ:

Ta có: 9 = 3 . 3 nên MN = 3 . AB.

Do đó độ dài đoạn thẳng MN có độ dài bằng 3 lần độ dài đoạn thẳng AB.

Vậy nếu ta chọn một đoạn thẳng có độ dài 3 cm làm đơn vị độ dài thì đoạn MN bằng 3 đơn vị độ dài đoạn thẳng có độ dài 3 cm.

Bài 12. Cho đoạn thẳng OA = 8 cm. Xác định vị trí của điểm B (bằng cách vẽ hình) nằm cách A một khoảng bằng 2 cm trên đường thẳng OA trong mỗi trường hợp sau:

a) Hai điểm O và B nằm cùng phía đối với điểm A;

b) Hai điểm O và B nằm khác phía đối với điểm A.

Lời giải:

Điểm B nằm cách A một khoảng bằng 2 cm hay độ dài AB = 2 cm.

a) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.

Mà hai điểm O và B nằm cùng phía đối với điểm A.

Nên điểm B nằm giữa hai điểm O và A.

* Cách xác định điểm B:

- Vẽ đoạn thẳng OA = 8 cm;

- Trên đoạn thẳng OA lấy điểm B sao cho AB = 2 cm.

Ta có hình vẽ:

b) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.

Mà hai điểm O và B nằm khác phía đối với điểm A.

Nên điểm A nằm giữa hai điểm O và B.

* Cách xác định điểm B:

- Vẽ đoạn thẳng OA = 8 cm;

- Trên tia đối của tia AO, lấy điểm B sao cho AB = 2 cm.

Ta có hình vẽ:

Bài 13. Tính độ dài đoạn thẳng AB biết rằng O là trung điểm của đoạn thẳng MN và OM = 4 cm.

Lời giải:

Vì I là trung điểm của đoạn thẳng AB nên .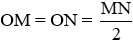

Do đó MN = 2 . OM = 2 . 4 = 8 cm.

Vậy MN = 8 cm.

Hình minh họa:

Bài 14. Cho điểm M nằm giữa hai điểm A và B, N là trung điểm của đoạn BC. Tính độ dài của đoạn AB, biết rằng AM = 3 cm và MN = 4 cm.

Lời giải:

Vì N là trung điểm của đoạn BM nên .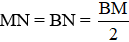

Suy ra BM = 2 . MN = 2 . 4 = 8 (cm)

Điểm M nằm giữa hai điểm A và B nên AB = AM + BM.

Suy ra AB = 3 + 8 = 11 (cm).

Vậy AB = 11 cm.

Hình minh họa:

Bài 15. Cho đoạn thẳng AB = 3 cm. Hãy vẽ điểm O sao cho:

a) B là trung điểm của đoạn OA.

b) A là trung điểm của của đoạn OB.

Lời giải: 

a) Vì B là trung điểm của OA nên: 

+) Điểm B nằm giữa hai điểm O và A.

+) AB = OB = 3 cm.

Vậy trên tia AB, ta lấy điểm O sao cho OB = 3 cm và B nằm giữa O và A.

Ta có hình minh họa:

b) Vì A là trung điểm OB nên:

+) Điểm A nằm giữa hai điểm O và B.

+) OA = AB = 3 cm.

Vậy trên tia BA, ta lấy điểm O sao cho OA = 3 cm và A nằm giữa O và B.

Ta có hình minh họa:

Bài 16. Kể tên các góc có trong hình vẽ sau. Trong đó góc nào là góc bẹt?

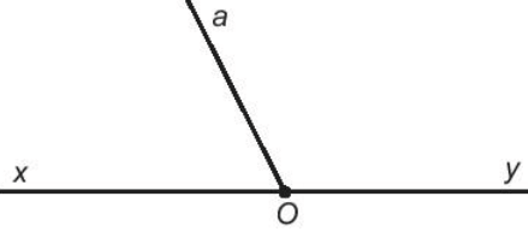
Lời giải:

Trong hình vẽ trên có ba tia Oa, Ox, Oy chung gốc O.

Cứ hai trong ba tia Oa, Ox, Oy sẽ tạo thành một góc.

Do đó các góc tạo thành là: góc xOy, góc xOa và góc aOy.

Ta thấy hai tia Ox và Oy là cùng nằm trên một đường thẳng nên góc xOy là góc bẹt.

Vậy các góc trong hình vẽ trên là: góc xOy, góc xOa và góc aOy. Trong đó, góc xOy là góc bẹt.

Bài 17. Viết tên các góc có đỉnh A, đỉnh C trong hình vẽ sau:

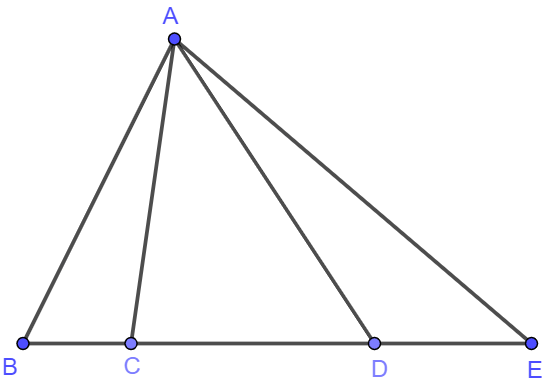
Lời giải:

- Đỉnh A

Các tia: AB, AC, AD, AE.

Góc tạo thành: .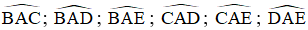

- Đỉnh C

Các tia: CA, CB, CD (tia CE trùng tia CD).

Góc tạo thành: .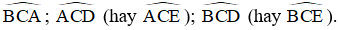

Vậy các góc có đỉnh A là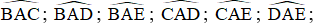 

Các góc có đỉnh C là .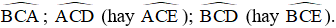

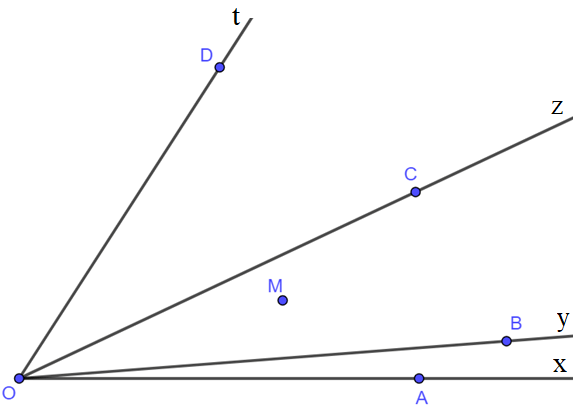
Bài 18. Cho bốn tia Ox, Oy, Oz, Ot chung gốc O và điểm M như hình vẽ dưới đây. Hỏi điểm M nằm trong những góc nào?

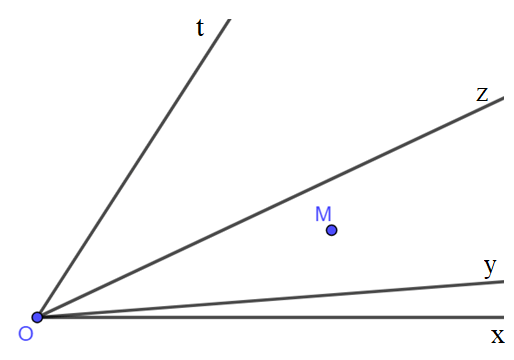
Lời giải:

Trên tia Ax, Ay, Az, At lần lượt lấy các điểm A, B, C, D (như hình vẽ).

Nối AB, AC, AD, BC, OM với nhau và kéo dài phía điểm M ta được tia OM (như hình vẽ).

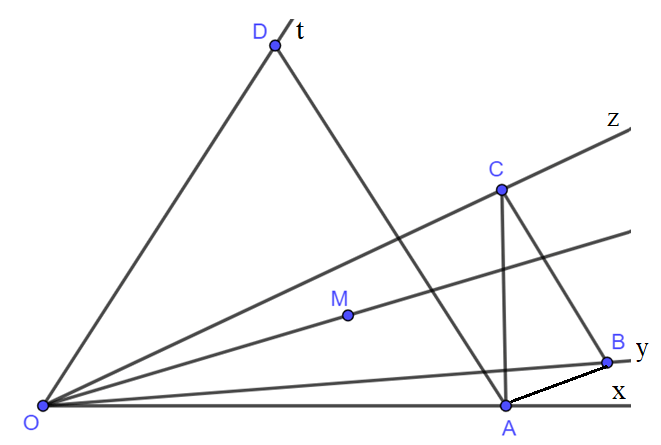
Nhận thấy:

+) Tia OM không cắt đoạn AB mà A ∈ Ox, B  Oy nên điểm M không phải là điểm trong của .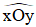

+) Tia OM cắt đoạn AC mà A Ox, C ∈ Oz nên điểm M là điểm trong của .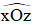

+) Tia OM cắt đoạn AD mà A Ox, D ∈ Ot nên điểm M là điểm trong của .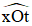

+) Tia OM cắt đoạn BC mà B Oy, C ∈ Oz nên điểm M là điểm trong của .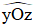

Vậy M là điểm trong của .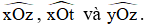

Bài 19. Góc tạo bởi kim phút và kim giờ tại thời điểm 2 giờ là bao nhiêu độ?

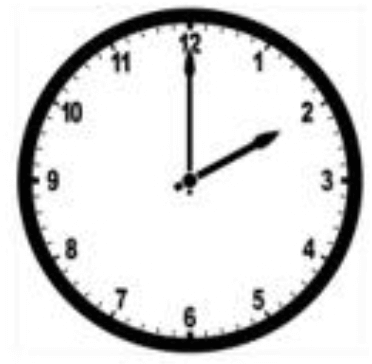
Lời giải:

Khi hai kim chỉ hai số liền kề nhau trên đồng hồ sẽ tạo thành góc 30^o. 

Chẳng hạn: Khi hai kim đồng hồ lần lượt chỉ số 1 và số 2 thì góc tạo bởi hai kim này là 30^o.

Tại thời điểm 2 giờ thì kim giờ chỉ số 2 và kim phút chỉ số 12.

Khi đó, góc tạo bởi kim giờ và kim phút lúc này là: 2 . 30^o = 60^o.

Vậy góc tạo bởi kim phút và kim giờ tại thời điểm 2 giờ là 60^o.

Bài 20. Tính tổng các số đo của ba góc .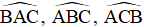

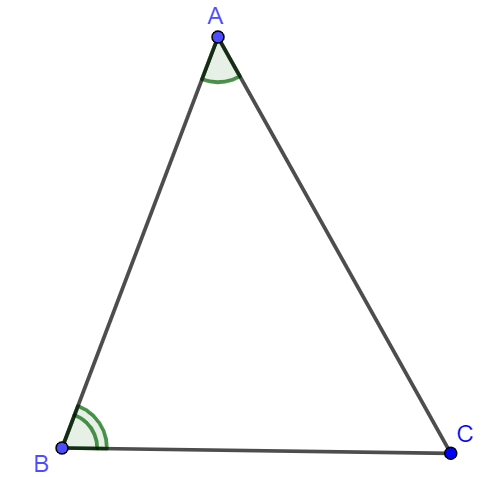
Lời giải:

Bài 21. Trong hình vẽ dưới đây, góc xOy là góc nhọn, góc tù hay góc vuông?

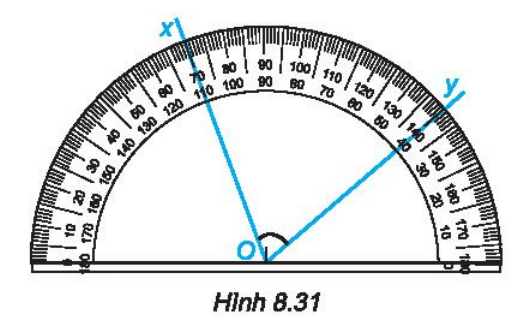
Lời giải:

* Ta tìm số đo góc xOy bằng hai cách:

Cách 1: Đo theo số đo vòng cung ngoài.

- Tia Ox tương ứng với vạch chỉ 70.

- Tia Oy tương ứng với vạch chỉ 140.

Lấy vạch chỉ số đo lớn trừ vạch chỉ số đo bé hơn, ta được: số đo của góc xOy là: 140^o – 70^o = 70^o.

Do đó, số đo của góc xOy là 70^o.

Cách 2: Đo theo số đo vòng cung trong.

- Tia Ox tương ứng với vạch chỉ 110.

- Tia Oy tương ứng với vạch chỉ 40.

Lấy vạch chỉ số đo lớn trừ vạch chỉ số đo bé hơn, ta được: số đo của góc xOy là: 110^o – 40^o = 70^o.

Do đó, số đo của góc xOy là 70^o.

* So sánh số đo hai góc:

Vì 70^o < 90^o nên góc xOy có số đo nhỏ hơn 90^o.

Vậy góc xOy là góc nhọn.

Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Chương 5: Phân số

Lý thuyết Chương 6: Số thập phân

Lý thuyết Chương 7: Hình học trực quan

Lý thuyết Chương 8: Hình học phẳng và các hình học cơ bản

Lý thuyết Chương 9: Một số yếu tố xác suất