Tailieumoi.vn xin giới thiệu tài liệu Trắc nghiệm Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản sách Chân trời sáng tạo. Tài liệu gồm 18 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:

Trắc nghiệm Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản

Phần 1. Trắc nghiệm Chương 8: Hình học phẳng và các hình học cơ bản

Câu 1: Cho hình vẽ sau. Chọn câu đúng.

A.P ∈ a; P ∈ c

B.Q ∈ b; Q ∈ c

C.Đường thẳng a cắt đường thẳng c tại điểm P

D.Không có hai đường thẳng nào cắt nhau trên hình vẽ

Trả lời:

Từ hình vẽ ta thấy P ∈ a; P ∈ c nên đáp án A sai; Q ∈ b; Q ∈ c nên đáp án B đúng.

Hai đường thẳng a và c cắt nhau tại điểm C nên đáp án C sai.

Đáp án D sai vì ta thấy có ba cặp đường thẳng cắt nhau trên hình vẽ là a và c, a và b, b và c.

Đáp án cần chọn là: B

Câu 2: Cho hai tia Ox và Oy đối nhau. Lấy điểm G trên tia Ox, điểm H trên tia Oy. Ta có:

A.Điểm G nằm giữa hai điểm O và H

B.Điểm O nằm giữa hai điểm G và H

C.Điểm H nằm giữa hai điểm O và G

D.Không có điểm nào nằm giữa hai điểm còn

Trả lời:

Ta có Ox và Oy là hai tia đối nhau (O ∈ xy) và G thuộc tia Ox, H thuộc tia Oy nên điểm O nằm giữa hai điểm G và H.

Đáp án cần chọn là: B

Câu 3: Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:

A.0

B.1 hoặc 2

C.4

D.3

Trả lời:

Với 3 đường thẳng phân biệt ta có các trường hợp sau:

+ Không có đường thẳng nào cắt nhau nên không có điểm chung.

+ Hai đường thẳng cắt nhau, đường thẳng còn lại không cắt hai đường thẳng đó, khi đó có 1 điểm chung.

+ Ba đường thẳng đó có đôi một cắt nhau thì có ba điểm chung.

Vậy không thể có trường hợp ba đường thẳng phân biệt bất kì mà có 4 điểm chung.

Đáp án cần chọn là: C

Câu 4: Cho hình vẽ. Em hãy chọn khẳng định sai:

A.NM và NI là hai tia đối nhau

B.IN và IM là hai tia trùng nhau

C.MN và MI là hai tia trùng nhau

D.MN và NI là hai tia trùng nhau

Trả lời:

Từ hình vẽ ta thấy các điểm M, N, I cùng thuộc một đường thẳng.

+) Hai tia NM và NI đối nhau vì chúng chung gốc N và tạo thành một đường thẳng, từ đó loại đáp án A.

+) Hai tia IN và IM trùng nhau vì chúng chung gốc I và có thêm điểm chung là N, từ đó loại đáp án B.

+) Hai tia MN và MI trùng nhau vì chúng chung gốc M và có thêm điểm chung là N, từ đó loại đáp án C.

+) Hai tia MN và NI không trùng nhau vì chúng không chung gốc.

Đáp án cần chọn là: D

Câu 5: Cho L là điểm nằm giữa hai điểm I và K. Biết IL = 2cm, LK = 5cm. Độ dài của đoạn thẳng IK là:

A.3cm

B.2cm

C.5cm

D.7cm

Trả lời:

Vì L nằm giữa I và K nên ta có:IL + LK = IK ⇒ IK = 2 + 5 = 7cm

Đáp án cần chọn là: D

Câu 6: Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?

A.1

B.2

C.3

D.Vô số

Trả lời:

Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước. Vậy có duy nhất 1 đường thẳng đi qua hai điểm A và B.

Đáp án cần chọn là: A

Câu 7: Cho hình vẽ. Em hãy chọn đáp án đúng.

A.A nằm giữa hai điểm B và C

B.B nằm giữa hai điểm A và C

C.C nằm giữa hai điểm A và B

D.Không có điểm nào nằm giữa hai điểm còn lại

Trả lời:

Quan sát hình vẽ ta thấy điểm B nằm giữa hai điểm A và C.

Đáp án cần chọn là: B

Câu 8: Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

A.Tia NM trùng với tia MP

B.Tia MP trùng với tia NP

C.Tia PM trùng với tia PN

D.Tia MN trùng với tia MP.

Trả lời:

Nhận xét:

+ Đáp án A: Hai tia NM và MP là hai tia không chung gốc nên loại đáp án A.

+ Đáp án B: Hai tia MP và NP là hai tia không chung gốc nên loại đáp án B.

+ Đáp án C: thấy hai tia PN và PM là hai tia cùng chung gốc P và tạo thành nửa đường thẳng nên hai tia PN và PM là hai tia trùng nhau, do đó chọn đáp án C.

+ Đáp án D: Hai tia MN và MP là hai tia chung gốc nhưng tạo thành một đường thẳng nên hai tia MN và MP là hai tia đối nhau, do đó loại đáp án D.

Đáp án cần chọn là: C

Câu 9: Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:

A.5

B.3

C.4

D.2

Trả lời:

Hình vẽ trên có các tia chung gốc B là: BA, Bx, By, BC và BD. Vậy có tất cả 5 tia chung gốc B.

Đáp án cần chọn là: A

Câu 10: Cho hình vẽ sau. Chọn câu đúng.

A.Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab

B.Hai đường thẳng xy và ab không có điểm chung

C.Đường thẳng xy cắt đường thẳng ab tại M

D.Đường thẳng xy và ab có hai điểm chung

Trả lời:

Ta thấy hai đường thẳng xy và ab cắt nhau tại M nên đáp án C đúng.

Đáp án cần chọn là: C

Câu 11: Cho đoạn thẳng BC = 32cm. Gọi G là trung điểm của đoạn thẳng BC, H là trung điểm của đoạn thẳng GC. Khi đó, độ dài của đoạn thẳng BH là

A.8cm

B.16cm

C.24cm

D.28cm

Trả lời:

Vì G là trung điểm của đoạn thẳng BC nên $\text{BG}=GC=\frac{1}{2}BC=\frac{1}{2}\cdot 32=16cm$

Vì H là trung điểm của đoạn thẳng GC nên $\text{GH}=HC=\frac{1}{2}GC=\frac{1}{2}\cdot 16=8cm$

Ta có G thuộc đoạn thẳng BC nên GB và GC là hai tia đối nhau. (1)

Vì H là trung điểm của GC nên H thuộc GC (2)

Từ (1) và (2) suy ra G là điểm nằm giữa hai điểm B và H.

⇒BG + GH = BH ⇒ 16 + 8 = BH ⇒ BH = 24cm

Đáp án cần chọn là: C

Câu 12: Biết IL = 4cm; LK = 5cm điều kiện để điểm I nằm giữa hai điểm L và K là:

A.IK = 1cm

B.IK = 9cm

C.IK = 2cm

D.IK = 3cm

Trả lời:

Điều kiện để điểm I nằm giữa hai điểm L và K là:
IL + IK = LK nên 4 + IK = 5 ⇒ IK = 5 – 4 = 1cm

Vậy điều kiện để điểm I nằm giữa hai điểm L và K là IK = 1cm

Đáp án cần chọn là: A

Câu 13: Cho điểm I thuộc đoạn thẳng AB. Biết AI = 5cm, AB = 8cm. Tính độ dài BI.

A.4cm

B.5cm

C.2cm

D.3cm

Trả lời:

Vì điểm I thuộc đoạn thẳng AB; AI = 5cm, AB = 8cm mà 5cm < 8cm nên AI < AB

Suy ra điểm I nằm giữa hai điểm A và B
⇒AI + IB = AB ⇒ 4cm + IB = 7cm ⇒ IB = 7cm − 4cm = 3cm

Đáp án cần chọn là: D

Câu 14: Lấy bốn điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:

A.3

B.10

C.12

D.4

Trả lời:

Từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được các đường thẳng đi qua hai điểm bất kì như sau:

+ Với điểm M ta có thể nối với các điểm: N, P, Q, K để tạo thành 4 đường thẳng phân biệt.

+ Với điểm N ta có thể nối với các điểm: P, Q, K để tạo thành 3 đường thẳng phân biệt.

+ Với điểm P ta có thể nối với các điểm: Q, K để tạo thành 2 đường thẳng phân biệt.

+ Với điểm Q ta có thể nối với điểm K để tạo thành 1 đường thẳng .

Vậy từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được tất cả:

4 + 3 + 2 + 1 = 10 đường thẳng phân biệt.

Đáp án cần chọn là: B

Câu 15: Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?

A.15

B.16

C.14

D.13

Trả lời:

Vì qua 2 điểm luôn vẽ được một đoạn thẳng

Nên qua 6 điểm vẽ được số đoạn thẳng là:

$\frac{6\left(6-1\right)}{2}=15$ (đoạn thẳng)

Đáp án cần chọn là: A

Câu 16: Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?

A.276

B.290

C.262

D.226

Trả lời:

Giả sử trong 24 điểm không có 3 điểm nào thẳng hàng tất cả vẽ được:
$\frac{24.(24-1)}{2}=276$ (đường thẳng)
Qua 6 điểm thẳng hàng vẽ được số đường thẳng là: $\frac{6.(6-1)}{2}=15$ (đường thẳng)
Nhưng qua 6 điểm thẳng hàng chỉ vẽ được một đường thẳng
Nên qua 24 điểm trong đó có 6 điểm thẳng hàng vẽ được:
276−15+1=262 (đường thẳng)
Đáp án cần chọn là: C

Câu 17: Cho M thuộc đoạn thẳng AB, AM = 4cm, AB = 6cm. Gọi O là trung điểm của đoạn AB.hiểu

Tính MO.

A.MO = 4cm

B.MO = 3cm

C.MO = 1cm

D.MO = 2cm

Trả lời:

+) Vì M ∈ AB nên M nằm giữa A và B

⇒AM + MB = AB ⇒ BM = AB – MB = 6 – 4 = 2cm.

+) Vì O là trung điểm của AB nên: $AO=OB=\frac{AB}{2}=\frac{6}{2}=3cm$ Vì O ∈ AB , M ∈ AB và AO < AM (3cm < 4cm)nên O nằm giữa A và M suy ra:

AO + OM = AM ⇒ OM = AM – AO = 4 – 3 = 1cm

Đáp án cần chọn là: C

Câu 18: Cho M thuộc đoạn thẳng AB, AM = 4cm, AB = 6cm. Gọi O là trung điểm của đoạn AB

Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.

A.Điểm I là trung điểm của OM

B.Điểm O nằm giữa I và P

C.IP = 2cm

D.Cả A, B, C đều đúng.

Trả lời:

+ ) Vì O ∈ AB , I ∈ AB và AO < AI (3cm < 3,5cm) nên O nằm giữa A và I suy ra:

AO + OI = AI ⇒ OI = AI – AO = 3,5 – 3 = 0,5cm(1)

Vì I ∈ AB , M ∈ AB và AI < AM (3,5cm < 4cm) nên I nằm giữa A và M suy ra:

AI + IM = AM ⇒ IM = AM – AI = 4 − 3,5 = 0,5cm (2)

Từ (1) và (2) suy ra OI = IM . (3)

Vì O nằm giữa A và I nên A và O nằm cùng phía đối với I . Mà I nằm giữa A và M nên A và M nằm khác phía đối với I ⇒ O và M nằm khác phía đối với I suy ra I nằm giữa M và O (4)

Từ (3) và (4) suy ra I là trung điểm của OM.

+) Vì P là trung điểm của AO nên: $OP=AP=\frac{AO}{2}=\frac{3}{2}=\mathrm{1,5}cm$

$\left\{\begin{array}{c}O,M\in AB\\ AO<AM(3cm<4cm)\end{array}\right.$⇒O nằm giữa A và M

Suy ra A và M nằm khác phía đối với O

Vì P là trung điểm của AO nên A, P cùng phía đối với O.

Vì I là trung điểm của OM nên I, M cùng phía đối với O.

Từ đó suy ra I nằm giữa O và P ⇒ OP + IO = IP ⇒ IP = 1,5 + 0,5 = 2cm

Đáp án cần chọn là: D

Phần 2. Lý thuyết Chương 8: Hình học phẳng và các hình học cơ bản

1. Điểm

Mỗi chấm nhỏ trên trang giấy, trên bảng, … cho ta hình ảnh của một điểm.

Người ta thường dùng các chữ cái in hoa A, B, C, D, …. để đặt tên cho điểm.

Chú ý: 

- Khi nói tới hai điểm mà không giải thích gì thêm, ta coi đó là hai điểm phân biệt.

- Từ những điểm, ta xây dựng được các hình. Mỗi hình là một tập hợp các điểm. Một điểm cũng được coi là một hình.

2. Đường thẳng

Dùng bút kẻ một vạch thẳng dọc theo mép thước ta sẽ được hình ảnh của một đường thẳng.

Chú ý: Ta thường dùng các chữ cái in hoa a, b, c, d, …. để đặt tên các đường thẳng.

3. Vẽ đường thẳng

Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

4. Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng

- Vẽ một điểm A trên giấy, dùng thước thẳng vẽ đường thẳng d đi qua điểm A. Khi đó, ta nói điểm A thuộc đường thẳng d (hoặc đường thẳng d chứa điểm A), hoặc điểm A nằm trên đường thẳng d), kí hiệu là: A∈d (như hình vẽ).

- Dùng thước thẳng vẽ đường thẳng d không đi qua điểm B.

Khi đó, ta nói điểm B không thuộc đường thẳng d (hoặc đường thẳng d không chứa điểm B hoặc điểm B không nằm trên đường thẳng d), kí hiệu là: B∉ d(như hình vẽ).

Chú ý: Nếu trên đường thẳng a có hai điểm A và B, ta cũng có thể gọi tên đường thẳng đó là đường thẳng AB hay BA (như hình vẽ).

5. Ba điểm thẳng hàng

- Ba điểm phân biệt A, B, C cùng thuộc một đường thẳng được gọi là ba điểm thẳng hàng.

Ta có hình vẽ:

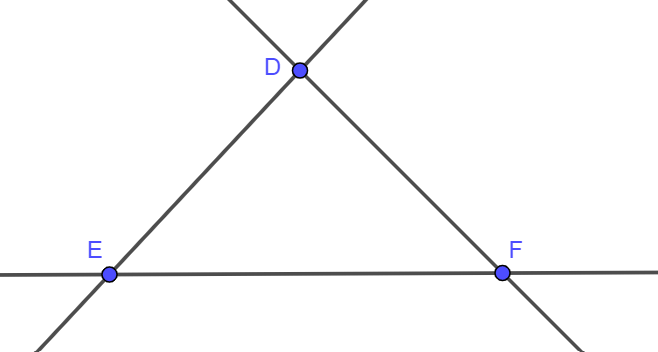
- Ba điểm D, E, F không cùng thuộc bất kì một đường thẳng nào được gọi là ba điểm không thẳng hàng.

Ta có hình vẽ:

6. Quan hệ giữa ba điểm thẳng hàng

Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.

Chẳng han: Với ba điểm A, B, C thẳng hàng. Điểm B nằm giữa hai điểm còn lại (như hình vẽ).

Trong hình vẽ trên:

- Các điểm B và C nằm cùng phía đối điểm A;

- Các điểm A và C nằm khác phía đối với điểm B.

7. Hai đường thẳng cắt nhau, song song

- Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.

Chú ý: Từ nay về sau, khi nói hai đường thẳng mà không nói gì thêm, ta hiểu đó là hai đường thẳng phân biệt.

8. Tia

Mỗi điểm O trên một đường thẳng chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc O.

Chú ý:

- Từ một điểm O kẻ một vạch thẳng về một phía của điểm O để biểu diễn một tia gốc O.

- Nếu A là một điểm tùy ý trên tia Ox, ta có thể gọi tia Ox là tia OA (như hình vẽ).

- Khi viết (đọc) tia, ta phải viết (đọc) gốc của tia trước.

9. Đoạn thẳng

Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa A và B.

Đoạn thẳng AB còn gọi là đoạn thẳng BA.

Hai điểm A, B gọi là hai đầu mút (hoặc hai đầu) của đoạn thẳng AB.

Ta có hình vẽ:

10. Độ dài đoạn thẳng

Cách đo độ dài đoạn thẳng AB:

Cho đoạn thẳng AB. Đặt cạnh của thước đi qua hai điểm A và B sao cho điểm A trùng với vạch số 0 của thước và nhìn xem điểm B trùng với vạch chỉ số bao nhiêu.

Giả sử điểm B trùng với vạch số 9 (như hình vẽ).

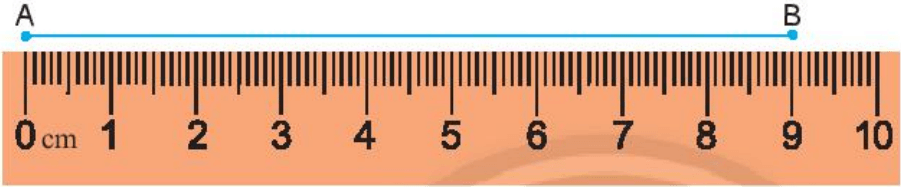
Khi đó, ta nói đoạn thẳng AB có độ dài là 9 cm. 

Kí hiệu AB = 9 cm hoặc BA = 9 cm.

Việc đo độ dài đoạn thẳng được thực hiện trên cơ sở so sánh nó với đoạn thẳng được chọn làm đơn vị đo hay đoạn thẳng đơn vị. 

Nhận xét:

- Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương.

- Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B.

- Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng 0.

Số đo độ dài của một đoạn thẳng không phải bao giờ cũng là số tự nhiên. 

11. So sánh hai đoạn thẳng

Ta so sánh hai đoạn thẳng bằng cách so sánh độ dài của chúng.

Chẳng hạn:

- Đoạn thẳng AB bằng đoạn thẳng CD và viết là AB = CD. 

- Đoạn thẳng EF dài hơn đoạn thẳng AB và viết là EF > AB.

- Đoạn thẳng CD ngắn hơn đoạn thẳng EF và viết là CD < EF.

12. Trung điểm của đoạn thẳng

Trung điểm của đoạn thẳng là điểm nằm giữa hai đầu mút của đoạn thẳng và cách đều hai đầu mút đó. Trung điểm của đoạn thẳng còn được gọi là điểm chính giữa của đoạn thẳng đó.

13. Cách vẽ trung điểm của đoạn thẳng

Giả sử ta cần vẽ trung điểm M của đoạn thẳng AB có độ dài 5 cm.

Cách 1:

- Đặt mép thước trùng với đoạn thẳng AB sao cho vạch 0 trùng với điểm A, khi đó điểm B trùng với vạch chỉ số 5 trên thước.

- Ta lấy điểm M trùng với vạch chỉ số 2,5 cm trên thước. Khi đó ta có M là trung điểm của đoạn thẳng AB (như hình vẽ).

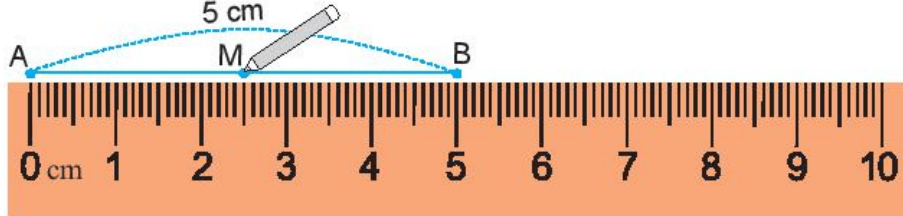
Cách 2: 

Vẽ đoạn thẳng AB trên giấy can sao cho điểm B trùng với điểm A. Giao của nếp gấp và đoạn thẳng AB chính là trung điểm M cần xác định.

14. Góc

Góc là hình tạo bởi hai tia chung gốc. 

Gốc chung của hai tia gọi là đỉnh của góc, hai tia gọi là hai cạnh của góc.

Kí hiệu: Góc xAy kí hiệu là  .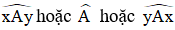

Chú ý: Trên hình vẽ, trong trường hợp nhiều góc có chung một đỉnh, người ta thường khoanh một cung giữa hai cạnh và đánh số: 1, 2, 3, … hoặc mỗi góc có khoanh những cung khác nhau chỉ các góc khác nhau đó.

15. Cách vẽ góc 

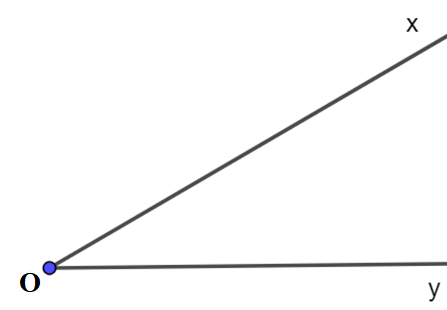
Để vẽ 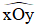, ta vẽ điểm O trên giấy hoặc bảng, từ điểm O vẽ hai tia Ox và Oy.

Ta có hình vẽ:

16. Góc bẹt 

Góc bẹt là hai cạnh của góc cùng nằm trên một đường thẳng.

17. Điểm trong của góc

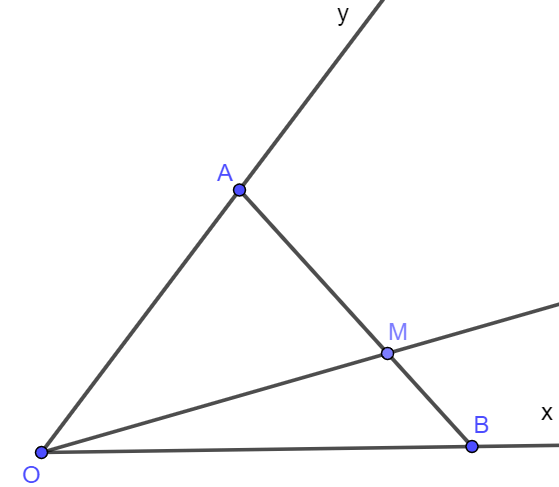
Cho góc xOy khác góc bẹt. Điểm M được gọi là điểm trong của góc xOy không bẹt nếu tia OM cắt một đoạn thẳng nối hai điểm trên hai cạnh tại một điểm nằm giữa hai điểm đó.

Ta có hình vẽ điểm M là điểm trong của góc xOy không bẹt.

18. Thước đo góc

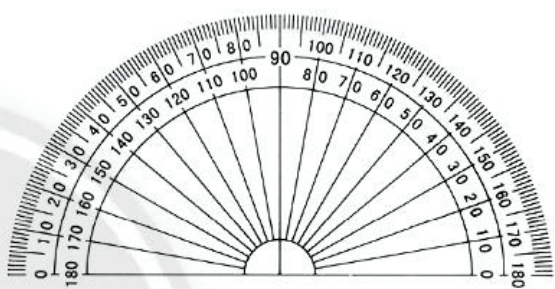
Trong hình vẽ trên là thước đo góc được dùng để đo hoặc vẽ góc. Thước có dạng một nửa hình tròn và được chia thành 180 phần bằng nhau bởi các vạch được ghi từ 0 đến 180. Mỗi một phần của thước ứng với 1 độ. Dấu ^o thay cho chữ “độ”.

Độ là đơn vị đo góc.

Ta gọi tâm của nửa hình tròn này là tâm của thước.

 19. Cách đo góc. Số đo góc

- Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

- Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc (như hình vẽ).

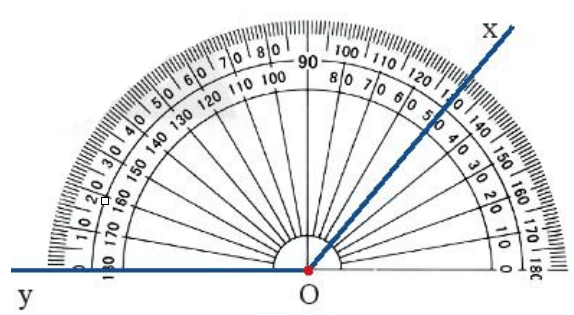
- Bước 3: Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.

Chẳng hạn: trong hình vẽ trên, tia Ox đi qua vạch chỉ số 130 của thước đo góc.

Do đó, số đo góc xOy là 130^o.

Nhận xét:

- Mỗi góc có một số đo. Số đo của góc bẹt là 180^o.

- Số đo của mỗi góc không vượt quá 180^o.

Chú ý:

- Trên thước đo góc, người ta ghi các số từ 0 đến 180 ở hai vòng cung theo hai chiều ngược nhau để việc đo góc được thuận tiện. Nếu một cạnh của góc trùng với cạnh ở nửa bên phải của thước đo thì chúng ta sử dụng thang ở bên trong, nếu nửa bên trái thì chúng ta sử dụng thang bên ngoài.

20. So sánh hai góc

Giả sử, 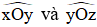 bằng nhau, kí hiệu là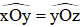 

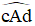 lớn hơn 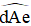, kí hiệu là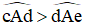 

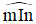 nhỏ hơn 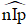, kí hiệu là .

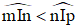21. Các góc đặc biệt 

- Góc có số đo bằng 90^o là góc vuông.

- Góc có số đo nhỏ hơn 90^o là góc nhọn.

- Góc có số đo lớn hơn 90^o là góc tù.

Xem thêm các bài trắc nghiệm Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Chương 5: Phân số

Trắc nghiệm Chương 6: Số thập phân

Trắc nghiệm Chương 7: Hình học trực quan

Trắc nghiệm Chương 8: Hình học phẳng và các hình học cơ bản

Trắc nghiệm Chương 9: Một số yếu tố xác suất