Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 7 sách Chân trời sáng tạo năm 2025 – 2026. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 7. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 1 Toán 7 Chân trời sáng tạo bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Chân trời sáng tạo
Năm học .................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Tìm phát biểu đúng trong các phát biểu sau:
A. B.
C. D.
Câu 2: Tìm , biết:
A. B. C. D.
Câu 3: Kết quả của phép tính:
A. B. C. D.
Câu 4: Cho hình vẽ bên dưới. Biết tia là tia phân giác của . Tính .
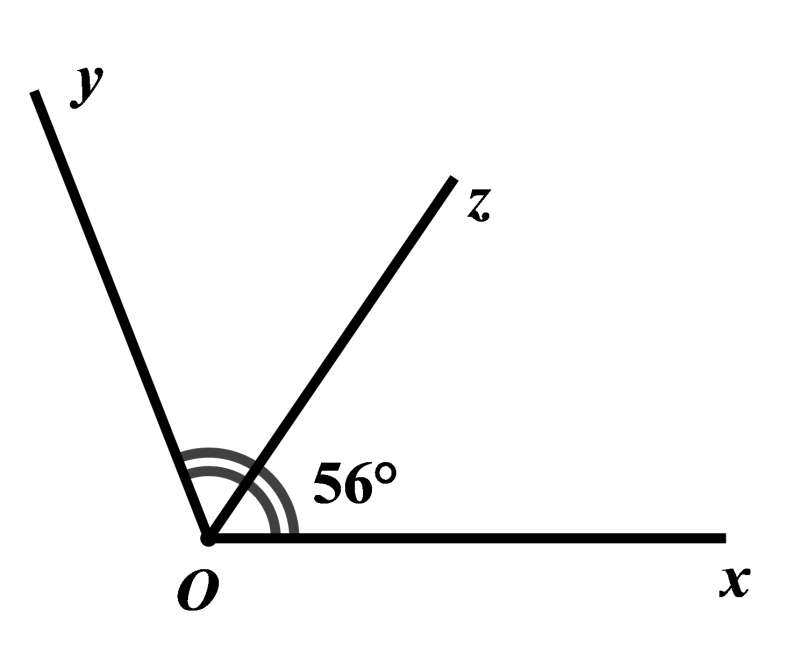
A. B. C. D.
Câu 5: Trong các hình vẽ dưới đây, liệt kê tất cả các hình là hình lăng trụ đứng tam giác hoặc hình lăng trụ đứng tứ giác?
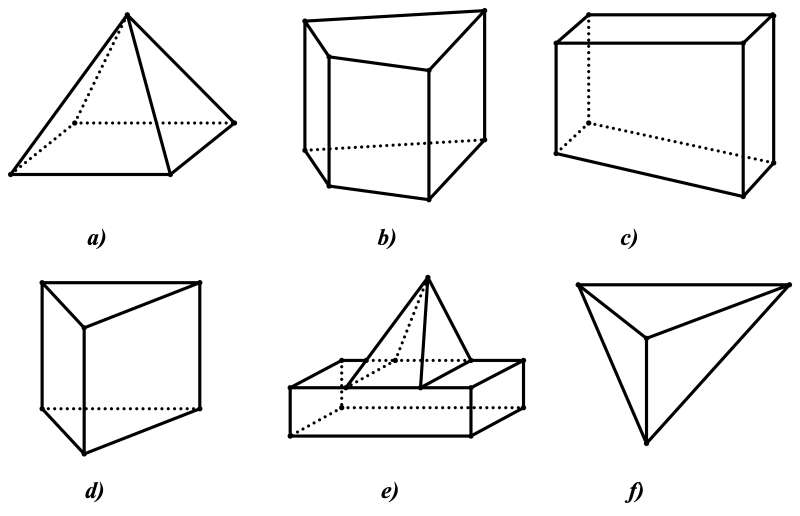
A. Tất cả 6 hình B. Hình a), c), e), f) C. Hình b), c), d) D. Hình b), d)
Câu 6:Một hình lập phương có thể tích là . Diện tích xung quanh của hình lập phương đó là:
A. B. C. D.
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) b)
c) d)
Bài 2: (1 điểm)
a) Sắp xếp các số sau theo thứ tự tăng dần: .
b) Sắp xếp các số sau theo thứ tự giảm dần: .
Bài 3: (2,0 điểm)
Tìm , biết:
a) b)
c) d)
Bài 4: (1,0 điểm)
Một giá đình xây bể chứa nước hình lăng trụ đứng, phần trong lòng bể có đáy là hình vuông cạnh 1,5m, chiều cao bể là 1m. Sau đó họ dùng các viên gạch men kịch thước cm, dày 1cm để ốp xung quanh bể và đáy bể. Hỏi gia đình đó cần ít nhất bao nhiêu viên gạch ốp và sau khi ốp bể chứa được khoảng bao nhiêu lít nước?
Bài 5: (1,0 điểm)
Cho , vẽ góc sao cho tia nằm giữa hai tia và .
a) Tính Tia có là tia phân giác của góc không? Vì sao?
b) Gọi tia là tia đối của tia . Tính số đo của
c) Gọi là tia phân giác của . Tính số đo của
Hướng dẫn giải:
I. TRẮC NGHIỆM ( 3 điểm)
|
1.A |
2.A |
3.B |
4.C |
5.A |
6.A |
Câu 1:
Phương pháp:
Tập hợp các số tự nhiên được kí hiệu là:
Tập hợp các số nguyên được kí hiệu là:
Tập hợp các số hữu tỉ được kí hiệu là: .
Cách giải:
+ là sai vì nên loại đáp án A.
+ là sai vì hoặc nên loại đáp án B.
+ là sai vì nên loại đáp án C.
+ là đúng nên chọn đáp án D.
Chọn A.
Câu 2:
Phương pháp:
Vận dụng quy tắc chuyển vế tìm giá trị của .
Cách giải:
Vậy
Chọn A.
Câu 3:
Phương pháp:
Thực hiện tính toán với biểu thức có chứa căn bậc hai.
Cách giải:
Chọn B.
Câu 4:
Phương pháp:
Vận dụng định nghĩa tia phân giác của một góc.
Cách giải:
Vì là tia phân giác của nên ta có:
Vậy
Chọn C.
Câu 5:
Phương pháp:
Hình lăng trụ đứng tam giác là hình hai mặt đáy là hình tam giác song song với nhau, ba mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau.
Hình lăng trụ đứng tứ giác là hình hai mặt đáy là hình tứ giác song song với nhau, bốn mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau.
Cách giải:
Từ các hình đã cho, ta thấy:
+ Hình vẽ b), c) là hình lăng trụ đứng tứ giác.
+ Hình vẽ d) là hình lăng trụ đứng tam giác.
Vậy hình vẽ b), c) và d) là các hình lăng trụ đứng tam giác hoặc lăng trụ đứng tứ giác.
Chọn A.
Câu 6:
Phương pháp:
Thể tích của hình lập phương có cạnh là được tính theo công thức: .
Diện tích xung quanh của hình lập phương có cạnh là được tính theo công thức:
Cách giải:
Gọi cạnh của hình lập phương là (điều kiện: )
Vì hình lập phương có thể tích là nên ta có:
Diện tích xung quanh của hình lập phương là:
Chọn A.
Phần II. Tự luận:
Bài 1:
Phương pháp:
a), b) Thực hiện phép cộng, trừ nhân chia số hữu tỉ.
c), d) Thực hiện phép tính có lũy thừa của một số hữu tỉ.
Chú ý:
Cách giải:
a)
b)
c)
d)
Bài 2:
Phương pháp:
Tính căn bậc hai số học của các căn bậc hai, sau đó so sánh.
Cách giải:
a)
+ Vì nên hay
Suy ra, (1)
+ Ta có:
Vì nên suy ra
Suy ra, (2)
Từ (1) và (2), suy ra
Vậy thứ tự tăng dần của các số là: .
b)
+ Vì nên hay
Ta có:
Vì nên hay
Vì nên (1)
Suy ra,
+ Ta có:
Vì nên
Suy ra, (2)
Từ (1) và (2), suy ra
Vậy thứ tự giảm dần của các số là: .
Bài 3:
Phương pháp:
Thực hiện phép tính, vận dụng quy tắc chuyển vế tìm
Cách giải:
a)
Vậy
b)
Vậy
c)
Vậy
d)
Vậy
Bài 4:
Phương pháp:
+ Tính diện tích: đáy bể, xung quanh bể và diện tích một viên gạch
Thực hiện phép chia ước lượng được số viên gạch cần ốp
+ Tính chiều dài cạnh đáy, chiều cao của bể sau khi ốp gạch
Tính thể tích sau khi ốp gạch
Cách giải:
* Diện tích đáy của bể là:
Diện tích xung quanh của bể là:
Diện tích của đáy bể và diện tích xung quanh của bể là:
Diện tích một viên gạch là:
Ta có:
Như vậy cần ít nhất viên gạch ốp.
* Chiều dài cạnh đáy sau khi ốp gạch là:
Chiều cao của bể sau khi ốp gạch là:
Thể tích của bể sau khi ốp gạch là:
Vậy sau khi ốp bể, bể chứa được khoảng 2147 lít nước.
Bài 5:
Phương pháp:
Vận dụng tính chất tia phân giác của một góc
Vận dụng kiến thức của hai góc kề nhau.
Cách giải:
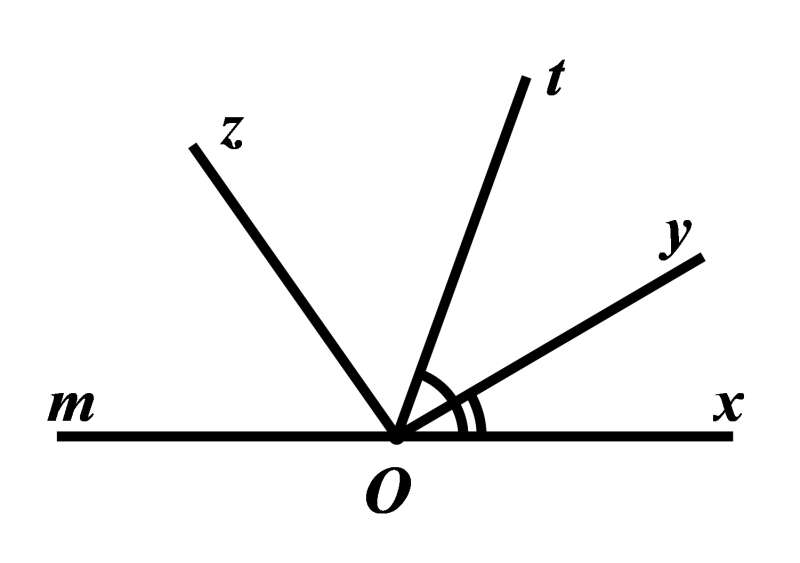
a) * Vì và là hai góc kề nhau nên ta có:
Vậy .
* Vì nên hai góc và không bằng nhau
Do đó, không là tia phân giác của .
b) Vì là tia đối của tia nên là góc bẹt và bằng .
Ta có: và là hai góc kề bù nên
Vậy
c) Vì là tia phân giác của (giả thiết) nên
Hai góc và kề nhau nên
Vậy
Đề thi giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Chân trời sáng tạo
Năm học .................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 2)
A. Đề kiểm tra giữa kỳ 1
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Trong các câu sau, câu nào đúng?
A.Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;
B. Số 0 là số hữu tỉ dương;
C.Số nguyên âm không phải là số hữu tỉ âm;
D. Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm.
Câu 2. Số đối của số hữu tỉ là
A. ;
B. ;
C. ;
D. .
Câu 3. Cho a = và b = .
Khẳng định nào sau đây là đúng?
A. a = b;
B. a > b;
C. a < b;
D. a ≤ b.
Câu 4. Cho các điểm A, B, C, D biểu diễn các số trên trục số như sau:
Điểm biểu diễn số là:
A. Điểm A;
B. Điểm B;
C. Điểm C;
D. Điểm D.
Câu 5. Cho biểu thức . Chọn khẳng định đúng?
A. Ta cần thực hiện phép tính trừ trước;
B. Ta cần thực hiện phép chia trước;
C. Ta cần thực hiện phép nhân trước;
D. Ta cần thực hiện phép cộng trước.
Câu 6. Kết quả của phép tính là:
A.
B.
C.
D.
Câu 7. Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?
A. 2 hình lập phương, 3 hình hộp chữ nhật;
B. 1 hình lập phương, 3 hình hộp chữ nhật;
C. 2 hình lập phương, 2 hình hộp chữ nhật;
D. 0 hình lập phương, 4 hình hộp chữ nhật.
Câu 8. Hãy chọn khẳng định sai.
Hình lập phương ABCD.A'B'C'D' có:
A. 8 đỉnh;
B. 4 mặt bên;
C. 6 cạnh;
D. 6 mặt.
Câu 9. Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm,
AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Câu 10. Chọn khẳng định đúng trong các khẳng định sau:
A. Hình lăng trụ đứng tam giác có mặt bên là hình tam giác;
B. Hình lăng trụ đứng tam giác là có mặt đáy là hình chữ nhật;
C. Hình lăng trụ đứng tam giác có mặt đáy là hình tam giác;
D. Hình lăng trụ đứng tam giác có mặt đáy là hình tứ giác.
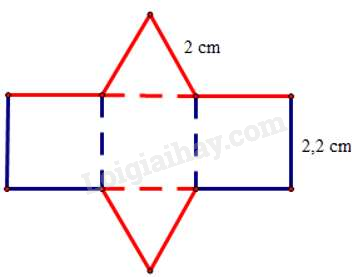
Câu 11. Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
Chiều cao của hình lăng trụ đứng là:
A. 2 cm;
B. 2,2 cm;
C. 4 cm;
D. 4,4 cm.
Câu 12. Chọn phát biểu sai:
A. Hai góc đối đỉnh thì bằng nhau;
B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh;
C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;
D. Hai góc bằng nhau thì đối đỉnh.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)Thực hiện phép tính (tính hợp lí nếu có thể):
a) ;
b) ;
c) .
Bài 2. (1,5 điểm) Tìm x, biết:
a) ;
b) ;
c) (x – 5)2 = (1 – 3x)2.
Bài 3. (0,75 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình vẽ.
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
a) Tính thể tích của khối gỗ.
b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Bài 5 (1,25 điểm) Cho hình vẽ dưới đây:
Biết rằng , và Om là tia phân giác của .
a) Kể tên các góc (khác góc bẹt) kề với góc zOm; góc kề bù với góc mOn.
b) Tính số đo của góc yOz.
Bài 6 (0,5 điểm) Một công ty phát triển kĩ thuật có một số thông báo rất hấp dẫn: Cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 17 ngày, công việc rất khó khăn nhưng tiền công cho dự án rất thú vị. Nhóm kĩ thuật viên được nhận làm dự án sẽ lựa chọn một trong hai phương án trả tiền công như sau:
– Phương án 1: Nhận một lần và nhận tiền công trước với mức tiền 170 triệu đồng;
– Phương án 2: Ngày đầu tiên nhận 3 đồng, ngày sau nhận gấp 3 lần ngày trước đó.
Em hãy giúp nhóm kỹ thuật viên lựa chọn phương án để nhận được nhiều tiền công hơn và giải thích tại sao chọn phương án đó.
B. Đáp án và hướng dẫn giải đề kiểm tra giữa kỳ 1
ĐÁP ÁN ĐỀ SỐ 01
I. Bảng đáp án trắc nghiệm
|
1. A |
2. A |
3. B |
4. A |
5. A |
6. D |
|
7. D |
8. C |
9. A |
10. C |
11. B |
12. D |
II. Hướng dẫn giải chi tiết trắc nghiệm
Câu 1.
Đáp án đúng là: A
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương. Đúng.
Số 0 là số hữu tỉ dương. Sai vì số hữu tỉ 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
Số nguyên âm không phải là số hữu tỉ âm. Sai vì mỗi số nguyên là một số hữu tỉ.
Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm. Sai vì tập hợp ℚ gồm các số hữu tỉ dương, số 0 và các số hữu tỉ âm.
Câu 2.
Đáp án đúng là: A
Số đối của số hữu tỉ là .
Câu 3.
Đáp án đúng là: B
Ta có:
(quy đồng mẫu số)
Vì ‒2 > ‒3 nên
Hay > .
Vậy > .
Câu 4.
Đáp án đúng là: A
Ta thấy đoạn thẳng đơn vị (chẳng hạn từ 0 đến 1) được chia thành 2 phần bằng nhau, ta lấy một đoạn làm đơn vị mới, đơn vị mới bằng đơn vị cũ.
Số hữu tỉ được biểu diễn bởi điểm nằm bên trái điểm 0 và cách 0 một đoạn bằng 3 đơn vị mới (hình vẽ trên). Điểm này chính là điểm A.
Câu 5.
Đáp án đúng là: A
Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.
Vì các phép tính cộng, nhân, chia ở ngoài ngoặc và phép tính trừ ở trong ngoặc, nên ta thực hiện phép tính trừ trước.
Vậy ta chọn phương án A.
Câu 6.
Đáp án đúng là: D
Ta có .
Câu 7.
Đáp án đúng là: D
Quan sát hình ta thấy không có hộp quà có dạng hình lập phương, có 4 hộp quà có dạng hình hộp chữ nhật đó là: hộp quà màu hồng nhạt, hộp quà màu xanh lam, hộp quà màu đỏ, hộp quà màu xanh lá cây.
Vậy chọn phương án D.
Câu 8.
Đáp án đúng là: C
Hình hộp chữ nhật này có 12 cạnh: AB; BC; CD; DA; A'B'; C'D'; B'C'; D'A'; AA'; BB'; CC'; DD'.
Do đó phương án C là khẳng định sai.
Vậy ta chọn phương án C.
Câu 9. Đáp án đúng là: A
Từ hình hộp chữ nhật ABCD.EFGH ta có các mặt của hình hộp này đều là hình chữ nhật.
Khi đó ta có:
HG = DC = AB = 4 cm;
HE = DA = BC = 2 cm;
GC = HD = AE = 4 cm.
Vậy HG = 4 cm, HE = 2 cm, GC = 4 cm.
Ta chọn đáp án A.
Câu 10.
Đáp án đúng là: C
Hình lăng trụ đứng tam giác có hai mặt đáy là hình tam giác nên C đúng.
Câu 11.
Đáp án đúng là: B
Hình lăng trụ đứng có tất cả 5 mặt nên đây là hình lăng trụ đứng tam giác.
Hình lăng trụ đứng tam giác có tất cả 6 đỉnh.
Câu 12.
Đáp án đúng là: D
Hai góc đối đỉnh là hai góc bằng nhau nên A đúng.
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia nên B đúng.
Hai đường thẳng xy và zt cắt nhau tại O (như hình vẽ trên). Ta có và ; và là hai cặp góc đối đỉnh. Do đó hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh nên C đúng.
Quan sát hình vẽ trên có: mà hai góc này ở vị trí kề nhau.
Do đó hai góc bằng nhau chưa chắc là hai góc ở vị trí đối đỉnh nên D sai.
Vậy ta chọn phương án D.
III. Hướng dẫn giải chi tiết tự luận
Bài 1. (1,5 điểm)
Hướng dẫn giải
a) .
b)
.
c)
Bài 2. (1,5 điểm)
a)
Vậy .
b)
–0,4 . (2x + 0,5) = –10
2x + 0,5 = (–10) : (–0,4)
2x + 0,5 = 25
2x = 25 – 0,5
2x = 24,5
x = 24,5 : 2
x = 12,25.
Vậy x = 12,25.
c) (x – 5)2 = (1 – 3x)2.
Trường hợp 1: x – 5 = 1 – 3x.
x + 3x = 1 + 5.
4x = 6.
.
.
Trường hợp 2: x – 5 = ‒(1 – 3x)
x – 5 = ‒1 + 3x
x ‒ 3x = ‒1 + 5.
‒2x = 4.
x = 4 : (‒2).
x = ‒2.
Vậy ; x = ‒2.
Bài 3. (0,75 điểm)
Để tính được số tiền bác Long dùng để sơn căn phòng ta phải tính được diện tích phần cần sơn.
Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.
Diện tích xung quanh của căn phòng là:
Sxq = 2. (5 + 6) . 3 = 66 (m2).
Diện tích phần cửa lớn và cửa sổ là:
1,2 . 2 + 1 . 1 = 3,4 (m2)
Diện tích phần cần sơn là:
66 – 3,4 = 62,6 (m2).
Tổng chi phí cần để sơn là:
62,6. 30 000 = 1 878 000 (đồng).
Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.
Bài 4. (1,5 điểm)
Đổi 3 dm = 30 cm; 4 dm = 40 cm; 5 dm = 50 cm;
1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm;
0,45 m = 45 cm.
a) Thể tích của khối gỗ là:
. 40 . 30 . 45 – . 20 . 15 . 25 = 23 250 (cm3).
b) Diện tích xung quanh của khối kim loại là:
(30 + 40 + 50).45 = 5 400 (cm2).
Diện tích xung quanh của cái lỗ là:
(20 + 15 + 25).45 = 2 700 (cm2).
Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:
.30.40 – .15.20 = 450 (cm2).
Diện tích bề mặt cần sơn là:
5 400 + 2 700 – 450 = 7 650 (cm2) = 0,765 (m2)
Vậy diện tích cần sơn là 0,765 mét vuông.
Bài 5 (1,25 điểm)
a) Các góc (khác góc bẹt) kề với góc zOm là: góc zOy, góc zOx, góc mOn.
Góc kề bù với góc mOn là: góc mOx.
b) Theo bài ta có Om là tia phân giác của
Suy ra (tính chất tia phân giác của một góc) (1)
Mà (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Suy ra
Ta có (hai góc kề nhau) và (hai góc kề bù)
Suy ra
Hay
Suy ra
Vậy số đo của góc yOz là 72°.
Bài 6 (0,5 điểm)
Theo phương án 2 ta có: Số tiền nhận được vào ngày thứ nhất là 3 đồng; ngày thứ hai là 3 . 3 = 32 đồng; ngày thứ ba là 32 . 3 = 33 đồng; … ; ngày thứ mười bảy là 317 đồng.
Như vậy số tiền công nhận được theo phương án 2 là:
T = 3 + 32 + 33 + … + 317
Suy ra 3T = 3 . (3 + 32 + 33 + … + 317)
= 3. 3 + 3. 32 + 3 . 33 + … + 3 . 317
= 32 + 33 + 34 + … + 318
Do đó 3T – T = (32 + 33 + 34 + … + 318) – (3 + 32 + 33 + … + 317)
Hay 2T = 318 – 3 = 387 420 489 – 3 = 387 420 486 (đồng)
Suy ra T = 193 710 243 (đồng) > 170 000 000 (đồng).
Vậy nhóm kĩ thuật viên nên chọn phương án 2 để nhận được nhiều tiền công hơn.
C. Ma trận đề kiểm tra giữa kỳ 1
|
TT |
Chủ đề |
Nội dung/Đơn vị kiến thức |
Mức độ đánh giá |
Tổng % điểm |
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||||||
|
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
||||
|
1 |
Số hữu tỉ |
Số hữu tỉ và tập hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ |
3 câu (TN1; TN2; TN3) 0,75đ |
1 câu (TN4) 0,25đ |
5,0 |
||||||
|
Các phép tính với số hữu tỉ |
1 câu (TN5) 0,25đ |
1 câu (TN6) 0,25đ |
2 câu (TL1a, TL2a) 1,0đ |
4 câu (TL1b, TL1c; TL2b, TL2c) 2,0đ |
1 câu (TL6) 0,5đ |
||||||
|
2 |
Các hình khối trong thực tiễn |
Hình hộp chữ nhật và hình lập phương |
2 câu (TN7, TN8) 0,5đ |
1 câu (TN9) 0,25 đ |
2 câu (TL3; 4) 2,25đ |
3,5 |
|||||
|
Lăng trụ đứngtam giác, lăng trụ đứng tứ giác |
2 câu (TN10, TN11) 0,5 đ |
||||||||||
|
3 |
Góc và đường thẳng song song |
Góc ở vị trí đặc biệt. Tia phân giác của một góc |
1 câu (TN12) 0,25 đ |
1 (TL5a) 0,5đ |
1 câu (TL5b) 0,75đ |
1,5 |
|||||
|
Tổng: Số câu Điểm |
9 2,25đ |
1 0,5đ |
3 0,75 đ |
2 1,0đ |
7 5,0đ |
1 0,5đ |
10,0 |
||||
|
Tỉ lệ % |
27,5% |
17,5% |
50% |
5% |
100% |
||||||
|
Tỉ lệ chung |
45% |
55% |
100% |
||||||||
Chú ý: Tổng tiết : 33 tiết
BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
|
TT |
Chương/Chủ đề |
Mức độ đánh giá |
Số câu hỏi theo mức độ nhận thức |
||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
1 |
Số hữu tỉ |
Số hữu tỉ và tập hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ |
Nhận biết: – Nhận biết được số hữu tỉ và tập hợp các số hữu tỉ. – Nhận biết được số đối của một số hữu tỉ. – Nhận biết được thứ tự trong tập hợp các số hữu tỉ. |
3 câu (TN1; TN2; TN3) |
|||
|
Thông hiểu: – Biểu diễn được số hữu tỉ trên trục số. |
1 câu (TN4) |
||||||
|
Vận dụng: – So sánh được hai số hữu tỉ. |
|||||||
|
Các phép tính với số hữu tỉ |
Thông hiểu: – Mô tả được phép tính luỹ thừa với số mũ tự nhiên của một số hữu tỉ và một số tính chất của phép tính đó (tích và thương của hai luỹ thừa cùng cơ số, luỹ thừa của luỹ thừa). – Mô tả được thứ tự thực hiện các phép tính, quy tắc dấu ngoặc, quy tắc chuyển vế trong tập hợp số hữu tỉ. |
1TN (TN5) |
1TN và 2TL (TN6, TL1a, TL2a) |
||||
|
Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số hữu tỉ. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số hữu tỉ trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Giải quyết được một số́vấn đề thực tiễn gắn với các phép tính về số hữu tỉ. (ví dụ: các bài toán liên quan đến chuyển động trong Vật lí, trong đo đạc,...). |
5TL (TL1b, TL1c; TL2b, TL2c; TL6) |
||||||
|
2 |
Các hình khối trong thực tiễn |
Hình hộp chữ nhật và hình lập phương |
Nhận biết: – Nhận biết được hình hộp chữ nhật, một số yếu tố cơ bản (đỉnh, cạnh, góc, đường chéo) của hình hộp chữ nhật và hình lập phương. |
2TN (TN7, TN8) |
|||
|
Thông hiểu Mô tả được một số yếu tố cơ bản (đỉnh, cạnh, góc, đường chéo) của hình hộp chữ nhật và hình lập phương. |
1TN (TN9) |
||||||
|
Vận dụng – Giải quyết được một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh của hình hộp chữ nhật, hình lập phương. |
|||||||
|
Lăng trụ đứngtam giác, lăng trụ đứng tứ giác |
Nhận biết – Nhận biết được một số yếu tố cơ bản (cạnh, góc, đường chéo) của hình chữ nhật, hình thoi, hình bình hành, hình thang cân. |
2TN (TN10, TN11) |
|||||
|
Thông hiểu: – Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của hình chữ nhật, hình thoi, hình bình hành, hình thang cân. |
|||||||
|
Vận dụng: – Giải quyết được một số vấn đề thực tiễn (đơn giản) gắn với việc tính chu vi và diện tích của các hình đặc biệt nói trên. |
2TL (TL3; 4) |
||||||
|
3 |
Góc và đường thẳng song song |
Góc ở vị trí đặc biệt. Tia phân giác của một góc |
Nhận biết: – Nhận biết được các góc ở vị trí đặc biệt (hai góc kề bù, hai góc đối đỉnh). – Nhận biết được tia phân giác của một góc. |
1TN (TN12) |
|||
|
Vận dụng: – Vận dụng được tính chất của các góc ở vị trí đặc biệt, tia phân giác để tính số đo góc. |
1TL (TL5) |
||||||
Đề thi giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 3
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Chân trời sáng tạo
Năm học .................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 3)
A. Đề kiểm tra giữa kỳ 1
I. Trắc nghiệm: Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1. Điền kí hiệu thích hợp vào chỗ trống: 12,5 … ℚ:
A. ∈;
B. ∉;
C. ⊂;
D. Một kí hiệu khác.
Câu 2. Tìm số a biết số đối của a là .
A. a = ;
B. a = ;
C. a = ;
D. a = .
Câu 3. Rút gọn biểu thức ta được kết quả là:
A. 55;
B. 56;
C. 85;
D. 58.
Câu 4. Những đồ vật sau có dạng hình gì?
A. Hình hộp chữ nhật;
B. Hình vuông;
C. Hình lập phương;
D. Hình chữ nhật.
Câu 5. Cho hình lập phương ABCD.MNPQ có độ dài cạnh là 2 cm. Tính tổng diện tích các mặt của hình lập phương.
A. 8 cm2;
B. 12 cm2;
C. 24 cm2;
D. 20 cm2.
Câu 6. Chọn phát biểu đúng trong các phát biểu sau:
A. Hình lăng trụ tam giác có 4 mặt, 6 đỉnh;
B. Hình lăng trụ tam giác có 5 mặt, 6 đỉnh;
C. Hình lăng trụ tam giác có 6 mặt, 5 đỉnh;
D. Hình lăng trụ tam giác có 4 mặt, 4 đỉnh.
Câu 7. Quan sát hình lập phương EFGH.MNPQ, biết MN = 3cm, độ dài các cạnh EF, NF bằng bao nhiêu?
A. EF = NF = 3 cm;
B. EF = 3 cm; NF = 6cm;
C. EF = NF = 6 cm;
D. Các đáp án trên đều sai.
Câu 8. Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.
Diện tích xung quanh của hình lăng trụ đứng trên là:
A. 36 cm2;
B. 30 cm2;
C. 36 cm3;
D. 30 cm3.
Câu 9. Cho các khẳng định sau:
(I). Hai góc đối đỉnh thì bằng nhau.
(II). Hai góc bằng nhau thì đối đỉnh.
(III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Số khẳng định đúng là:
A. 1;
B. 2;
C. 3;
D. Không có khẳng định nào đúng.
Câu 10. Cho ; Oy là tia phân giác . Khi đó bằng:
A. 90°;
B. 120°;
C. 15°;
D. 60°.
Câu 11. Số tự nhiên n thỏa mãn là:
A. 12;
B. 7;
C. 1;
D. 8.
Câu 12. Số nào dưới đây là giá trị của biểu thức ?
A. 2;
B. –1;
C. 1;
D. 0.
II. Tự luận (7,0 điểm)
Bài 1. (1,75 điểm)Thực hiện phép tính (tính hợp lý nếu có thể):
a) ;
b) ;
c) .
Bài 2. (1,0 điểm) Tìm x biết:
a) ;
b) (2x – 8)2 022 = (3 – 4x)2 022.
Bài 3. (1,25 điểm) Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng 6 m. Đường cao của đáy (là chiều rộng của nhà kho) bằng 5 m. Các cạnh đáy của hình thang vuông dài 3 m và 4 m. Tính thể tích của nhà kho.
Bài 4. (1,5 điểm) Một phòng học hình hộp chữ nhật có chiều dài 8 m, chiều rộng 5 m, chiều cao 4 m. Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là 10 m2. Tính diện tích phải quét vôi.
Bài 5 (1 điểm) Cho góc bẹt . Gọi Oc là tia phân giác của ; Ox là phân giác của ; Oy là phân giác của . Tính số đo .
Bài 6 (0,5 điểm) Tính giá trị nhỏ nhất của biểu thức M = (x – 5)2 + 7.
B. Đáp án và hướng dẫn giải đề kiểm tra giữa kỳ 1
ĐÁP ÁN ĐỀ SỐ 3
I. Bảng đáp án trắc nghiệm
|
1. A |
2. C |
3. D |
4. B |
5. C |
6. B |
|
7. A |
8. C |
9. B |
10. D |
11. A |
12. D |
II. Hướng dẫn giải chi tiết trắc nghiệm
Câu 1.
Đáp án đúng là: A
Ta có: .
Vì 25; 2 ∈ ℤ; 2 ≠ 0 nên ℚ hay 12,5 ∈ ℚ.
Chọn đáp án A.
Câu 2.
Đáp án đúng là: C
Ta có: .
Số đối của số là .
Hay số đối của số là .
Vậy .
Chọn đáp án C.
Câu 3.
Đáp án đúng là: D
Ta có .
Chọn đáp án D.
Câu 4.
Đáp án đúng là: B
Những đồ vật trong hình trên có 6 mặt đều là hình hộp chữ nhật nên chúng có dạng hình hộp chữ nhật.
Chọn đáp án B.
Câu 5.
Đáp án đúng là: C
Hình lập phương đã cho gồm 6 mặt bằng nhau. Mỗi mặt là hình vuông có độ dài cạnh là 2 cm.
Diện tích mỗi mặt là: 22 = 4 (cm2).
Tổng diện tích các mặt của hình lập phương là:
4 . 6 = 24 (cm2).
Vậy tổng diện tích các mặt của hình lập phương là 24 cm2.
Chọn đáp án C.
Câu 6.
Đáp án đúng là: B
Hình lăng trụ tam giác ABC.DEF có:
+ 5 mặt: ABC; DEF; ABED; BCFE; ACFD
+ 6 đỉnh: A, B, C, D, E, F.
Chọn đáp án B.
Câu 7.
Đáp án đúng là: A
Vì hình lập phương nên tất cả các mặt đều là các hình vuông bằng nhau.
Khi đó, tất cả các cạnh của hình lập phương đều bằng nhau.
Suy ra: EF = NF = MN.
Mà MN = 3 cm nên EF = NF = 3 cm.
Vậy EF = NF = 3 cm.
Câu 8.
Đáp án đúng là: C
Diện tích xung quanh hình lăng trụ đứng đó là:
Sxq = (3 + 4 + 5) . 3 = 12 . 3 = 36 (cm2)
Chọn đáp án C.
Câu 9.
Đáp án đúng là: B
Hai góc đối đỉnh thì bằng nhau nhưng hai góc bằng nhau thì chưa chắc đã đối đỉnh. Dưới đây là một số ví dụ về trường hợp hai góc bằng nhau nhưng không đối đỉnh:
Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Do đó các khẳng định (I), (III) đúng. Khẳng định (II) sai.
Vậy có 2 khẳng định đúng.
Chọn đáp án B.
Câu 10.
Đáp án đúng là: D
Vì Oy là tia phân giác nên .
Suy ra .
Vậy .
Chọn đáp án D.
Câu 11.
Đáp án đúng là: A
Ta có
Do đó n = 12.
Chọn đáp án A.
Câu 12.
Đáp án đúng là: D
Ta có:
= 1 + (‒1) = 0.
Vậy ta chọn đáp án D.
III. Hướng dẫn giải chi tiết tự luận
Bài 1. (1,75 điểm)
Hướng dẫn giải
a)
.
b)
.
c)
Bài 2. (1,0 điểm)
Hướng dẫn giải
a)
Vậy .
b) (2x – 8)2 022 = (3 – 4x)2 022
2x – 8 = 3 – 4x.
2x + 4x = 3 + 8.
6x = 11.
.
Vậy .
Bài 3. (1,25 điểm)
Hướng dẫn giải
Gọi nhà kho có dạng hình lăng trụ đứng ABCD.A’B’C’D’.
Diện tích đáy hình lăng trụ là:
(cm2)
Thể tích nhà kho là:
Vkho = SABCD . AA’ = 17,5 . 6 = 105 (cm3)
Vậy thể tích nhà kho là 105 cm3.
Bài 4. (1,25 điểm)
Hướng dẫn giải
Gọi căn phòng là hình hộp chữ nhật ABCD.A’B’C’D’.
Chu vi căn phòng hình chữ nhật là:
2 . (8 + 5) = 26 (m)
Diện tích xung quanh của căn phòng là:
Sxq = 26 . 4 = 104 (m2)
Diện tích trần của căn phòng là:
Strần = 8 . 5 = 40 (m2)
Diện tích phải quét vôi là:
S = Sxq + Strần – 10 = 104 + 40 – 10 = 134 (m2).
Vậy diện tích phải quét vôi là 134 m2.
Bài 5 (1 điểm)
Hướng dẫn giải
Vì Oc là tia phân giác của nên .
Suy ra (vì là góc bẹt)
Vì Ox là phân giác của nên:
.
Vì Oy là phân giác của nên:
.
Ta có tia Oc nằm giữa hai tia Ox và Oy nên:
.
Vậy .
Bài 6 (0,5 điểm)
Hướng dẫn giải
Ta có (x – 5)2 ≥ 0 nên (x – 5)2 + 7 ≥ 7.
Dấu "=" xảy ra khi (x – 5)2 = 0
Suy ra x – 5 = 0
Do đó x = 5.
Vậy giá trị nhỏ nhất của biểu thức M bằng 7 khi x = 5.
C. Ma trận đề kiểm tra giữa kì 1
|
TT |
Chủ đề |
Nội dung/Đơn vị kiến thức |
Mức độ đánh giá |
Tổng % điểm |
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||||||
|
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
||||
|
1 |
Số hữu tỉ
|
Số hữu tỉ và tập hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ |
3 câu (TN1; 2; 3) 0,75đ |
|
|
|
|
|
|
|
4,5 |
|
Các phép tính với số hữu tỉ |
|
|
2 câu (TN11; 12) 0,5đ |
|
|
5 câu (TL 1a, b, c; 2a, b) 2,75đ |
|
1 câu (TL6) 0,5đ |
|||
|
2 |
Các hình khối trong thực tiễn
|
Hình hộp chữ nhật và hình lập phương |
2 câu (TN4; 7) 0,5đ
|
|
1 câu (TN5) 0,25 đ |
|
|
|
|
|
4,0 |
|
Lăng trụ đứng tam giác, lăng trụ đứng tứ giác |
2 câu (TN6; 8) 0,5 đ |
|
|
|
|
2 câu (TL3; 4) 2,75đ |
|
|
|||
|
3 |
Góc và đường thẳng song song
|
Góc ở vị trí đặc biệt. Tia phân giác của một góc |
2 câu (TN9; 10) 0,5 đ |
1 câu (TL5) 1,0đ |
|
|
|
|
|
|
1,5 |
|
Tổng: Số câu Điểm |
9 2,25đ |
1 1,0đ |
3 0,75 đ |
|
|
7 5,5đ |
|
1 0,5đ |
10,0 |
||
|
Tỉ lệ % |
32,5% |
7,5% |
55% |
5% |
100% |
||||||
|
Tỉ lệ chung |
40% |
60% |
100% |
||||||||
Chú ý: Tổng tiết : 33 tiết
BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TOÁN – LỚP 7
|
TT |
Chương/Chủ đề |
Mức độ đánh giá |
Số câu hỏi theo mức độ nhận thức |
||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
1 |
Số hữu tỉ |
Số hữu tỉ và tập hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ |
Nhận biết: – Nhận biết được tập hợp các số hữu tỉ. |
1TN (TN1) |
|
|
|
|
– Nhận biết được số đối của một số hữu tỉ. |
1TN (TN2) |
|
|
|
|||
|
– Nhận biết được thứ tự trong tập hợp các số hữu tỉ. |
|
|
|
|
|||
|
Thông hiểu: – Biểu diễn được số hữu tỉ trên trục số. |
|
|
|
|
|||
|
Vận dụng: – So sánh được hai số hữu tỉ. |
|
|
|
|
|||
|
Các phép tính với số hữu tỉ |
Thông hiểu: – Phép tính luỹ thừa với số mũ tự nhiên của một số hữu tỉ và một số tính chất của phép tính đó (tích và thương của hai luỹ thừa cùng cơ số, luỹ thừa của luỹ thừa). |
1TN (TN3) |
|
|
|
||
|
– Thứ tự thực hiện các phép tính, quy tắc dấu ngoặc, quy tắc chuyển vế trong tập hợp số hữu tỉ. |
|
|
|
|
|||
|
Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số hữu tỉ. |
|
|
|
1TL (TL1a, b, c) |
|||
|
– Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số hữu tỉ trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). |
|
|
|
1TL (TL2a, b) |
|||
|
– Giải quyết được một số vấn đề thực tiễn gắn với các phép tính về số hữu tỉ. (ví dụ: các bài toán liên quan đến chuyển động trong Vật lí, trong đo đạc,...). |
|
|
|
|
|||
|
2 |
Các hình khối trong thực tiễn |
Hình hộp chữ nhật và hình lập phương |
Nhận biết: Mô tả được một số yếu tố cơ bản (đỉnh, cạnh, góc, đường chéo) của hình hộp chữ nhật và hình lập phương. |
2TN (TN4; 7)
|
|
|
|
|
Thông hiểu – Giải quyết được một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh của hình hộp chữ nhật, hình lập phương, hình lăng trục đứng tam giác, tứ giác. |
1TN (TN5)
|
|
|
|
|||
|
Lăng trụ đứng tam giác, lăng trụ đứng tứ giác |
Nhận biết – Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của hình chữ nhật, hình thoi, hình bình hành, hình thang cân. |
2TN (TN6; 8)
|
|
|
|
||
|
Thông hiểu: – Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của hình chữ nhật, hình thoi, hình bình hành, hình thang cân. |
|
|
|
|
|||
|
Vận dụng : – Giải quyết được một số vấn đề thực tiễn (đơn giản) gắn với việc tính chu vi và diện tích của các hình đặc biệt nói trên. |
|
|
2TL (TL3; 4) |
|
|||
|
3 |
Góc và đường thẳng song song
|
Góc ở vị trí đặc biệt. Tia phân giác của một góc |
Nhận biết : – Nhận biết được các góc ở vị trí đặc biệt (hai góc kề bù, hai góc đối đỉnh). |
1TN (TN9) |
|
|
|
|
– Nhận biết được tia phân giác của một góc. |
1TN (TN5) 1TL (TL5) |
|
|
|
|||
Lưu ý:
- Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
- Các câu hỏi ở cấp độ vận dụng và vận dụng cao là câu hỏi tự luận.
- Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
Đề thi giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 4
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Chân trời sáng tạo
Năm học .................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 4)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Chọn câu sai trong các câu sau:
A. Số là số hữu tỉ;
B. Mọi số nguyên đều là số hữu tỉ;
C. Số là số hữu tỉ;
D. Số hữu tỉ là các số được viết dưới dạng với a, b∈Z, b ≠ 0.
Câu 2. Số đối của các số hữu tỉ sau: 0,5; lần lượt là:
A. 0,5; ;
B. −0,5; ;
C. −0,5; ;
D. 0,5; .
Câu 3. Trong các số sau, số nào có cùng biểu diễn với số hữu tỉ ?
A. ;
B. ;
C. ;
D. Cả A và C đều đúng.
Câu 4. Điểm A trong hình dưới đây biểu diễn số hữu tỉ nào?
A. ;
B. ;
C. ;
D. – 1.
Câu 5. Cho biểu thức (–8)2 : {0,25 – 0,18 : [(52 + 22) : 0,11 – 20230]} .
Ta cần thực hiện phép tính nào trước?
A. Phép cộng;
B. Phép chia;
C. Tất cả các lũy thừa có trong biểu thức;
D. Phép trừ.
Câu 6. Số là kết quả của phép tính nào dưới đây?
A. ;
B. ;
C. ;
D. .
Câu 7. Chọn phương án sai.
A. Ống bút có dạng hình lăng trụ đứng tứ giác;
B. Ống bút có dạng hình hộp chữ nhật;
C. Ống bút có dạng hình lập phương;
D. Ống hút có dạng hình lăng trụ đứng tam giác.
Câu 8. Hình lập phương có bao nhiêu đường chéo?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 9. Tấm bìa nào sau đây gấp được thành hình lập phương?
A. Hình a;
B. Hình b;
C. Hình c;
D. Không có hình nào.
Câu 10. Một hình lăng trụ đứng có tất cả 6 mặt. Hình lăng trụ này có bao nhiêu đỉnh?
A. 5 đỉnh;
B. 6 đỉnh;
C. 8 đỉnh;
D. 10 đỉnh.
Câu 11. Cho hình lăng trụ đứng ABC.DEF biết AB = 3 cm; AC = 4 cm; BC = 5 cm. Chu vi tam giác DEF là:
A. 10 cm;
B. 11 cm;
C. 12 cm;
D. 13 cm.
Câu 12. Chọn phát biểu sai:
A. Hai góc đối đỉnh thì bằng nhau;
B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh;
C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;
D. Hai góc bằng nhau thì đối đỉnh.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)Thực hiện phép tính (tính hợp lí nếu có thể):
a) ;
b) ;
c)
Bài 2. (1,5 điểm) Tìm x, biết:
a) ;
b) ;
c) .
Bài 3. (1,25 điểm) Một chiếc bục gỗ có các kích thước như hình vẽ sau:
a) Tính thể tích của chiếc bục đó.
b) Người ta muốn sơn các bề mặt của chiếc bục (trừ mặt tiếp xúc với mặt đáy). Tính diện tích cần sơn.
Bài 4. (1,0 điểm) Một ngôi nhà có các kích thước như hình vẽ dưới đây:
Tính khoảng không bên trong ngôi nhà và diện tích tất cả các mặt (trừ mặt tiếp xúc với mặt đất) của ngôi nhà.
Bài 5 (1,25 điểm)
Cho hình vẽ dưới đây.
Biết tia Ot, Ou lần lượt là tia phân giác của góc zOy, góc tOy.
a) Kể tên các góc kề (khác góc bẹt) kề với góc zOu; góc kề bù với góc xOz.
b) Tính số đo của góc xOz.
Bài 6 (0,5 điểm) Cho Chứng minh rằng
Đề thi giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 5
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Chân trời sáng tạo
Năm học .................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 5)
I. Trắc nghiệm: Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1. Số nào sau đây biểu diễn số hữu tỉ
A.
B.
C.
D.
Câu 2. Cho hình vẽ, biết A và B biểu diễn hai số đối nhau. Điểm B biểu diễn số hữu tỉ nào:
A. ;
B. ;
C. ‒2;
D. 2.
Câu 3. Số cần điền vào dấu “?” trong là:
A. 6;
B. 5;
C. 2;
D. 1.
Câu 4. Lan có một tấm bìa có kích thước như hình vẽ, An có thể gấp tấm bìa thành hình gì?
A. Hình hộp chữ nhật;
B. Hình chữ nhật;
C. Hình vuông;
D. Hình lập phương.
Câu 5.Cho hình hộp chữ nhật có chiều dài 20 m, chiều rộng 8 m, chiều cao 15 m. Tính diện tích xung quanh của hình hộp chữ nhật.
A. 840 m2;
B. 820 m2;
C. 760 m2;
D. 780 m2.
Câu 6. Chọn khẳng định đúng trong các khẳng định sau:
A. Hình lăng trụ đứng tam giác có mặt bên là hình tam giác;
B. Hình lăng trụ đứng tam giác là có mặt đáy là hình chữ nhật;
C. Hình lăng trụ đứng tam giác có mặt đáy là hình tam giác;
D. Hình lăng trụ đứng tam giác có mặt đáy là hình tứ giác.
Câu 7. Cho hình lập phương có thể tích là 343 cm3. Tính diện tích một mặt của hình lập phương.
A. 8 cm2;
B. 12 cm2;
C. 16 cm2;
D. 64 cm2.
Câu 8. Quan sát hình hộp chữ nhật ABCD.A'B'C'D' (Hình dưới). Hãy kể tên các mặt đáy của hình hộp?
A. Các mặt đáy: ABCD, A'B'C'D';
B. Các mặt đáy: ABB'A', CDD'C';
C. Các mặt đáy: ABCD, BCC'B';
D. Các mặt đáy: A'B'C'D', BCC'B'.
Câu 9. Cho hình vẽ sau, góc đối đỉnh với là:
A. ;
B. ;
C. ;
D. .
Câu 10. Cho hình vẽ sau:
Tia Oy là tia phân giác của góc nào?
A. ;
B. ;
C. ;
D. .
Câu 11. Rút gọn biểu thức 49 . 527 bằng:
A. 203;
B. 209;
C. 5003;
D. 5009.
Câu 12. Phép tính nào dưới đây có kết quả bằng ?
A. ;
B. ;
C. ;
D. .
II. Tự luận (7,0 điểm)
Bài 1. (1,75 điểm)Thực hiện phép tính(tính bằng cách hợp lí nếu có thể):
a) ;
b) ;
c) .
Bài 2. (1,0 điểm) Tìm x, biết:
a) ;
b) .
Bài 3. (1,25 điểm) Một khối kim loại có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Tính thể tích của khối kim loại vuông (m3) (không tính cái lỗ) biết khối kim loại dài 0,45 m.
Bài 4. (1,5 điểm) Cho một căn phòng có dạng hình hộp chữ nhật. Biết chiều dài, chiều rộng căn phòng lần lượt là 3 m và 2 m và mặt bên chứa cạnh 3 m có đường chéo dài 5 m.
a) Tính diện tích mặt sàn căn phòng.
b) Để sơn xung quanh căn phòng cần trả bao nhiêu tiền công cho thợ sơn biết giá công sơn là 50 000 đồng cho mỗi m2.
Bài 5 (1,0 điểm)Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết . Tính .
Bài 6 (0,5 điểm)Tính giá trị của .
Đề thi giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 6
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Chân trời sáng tạo
Năm học .................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 6)
Phần trắc nghiệm (3 điểm)
Câu 1: Chọn đáp án đúng
|
A. |
B. |
|
C. |
D. |
Câu 2: Kết quả của phép tính: là
|
A. |
B. |
|
C. |
D. |
Câu 3: Kết quả của phép tính: - 0,35. là
|
A. - 0,1 |
B. -1 |
|
C. -10 |
D. -100 |
Câu 4: Kết quả của phép tính: là
|
A. -6 |
B. |
|
C. |
D. |
Câu 5: Kết quả phép tính: là
|
A. |
B. |
|
C. |
D. |
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
|
A. - 1,8 |
B. 1,8 |
|
C. 0 |
D. - 2,2 |
Câu 7: Kết quả phép tính:
|
A. . |
B. . |
|
C. . |
D. . |
Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?

A. 2 hình lập phương, 3 hình hộp chữ nhật;
B. 1 hình lập phương, 3 hình hộp chữ nhật;
C. 2 hình lập phương, 2 hình hộp chữ nhật;
D. 0 hình lập phương, 4 hình hộp chữ nhật.
Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:
|
A. 8 đỉnh |
B. 4 mặt bên |
|
C. 6 cạnh |
D. 6 mặt |
Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Câu 11: Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
Chiều cao của hình lăng trụ đứng là:
|
A. 2 cm |
B. 2,2 cm |
|
C. 4 cm |
D. 4,4 cm |
Câu 12: Chọn phát biểu sai:
A. Hai góc đối đỉnh thì bằng nhau;
B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc
đối đỉnh;
C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;
D. Hai góc bằng nhau thì đối đỉnh.
Phần tự luận (7 điểm)
Bài 1: (1 điểm) Tìm x, biết
|
a. |
b. 100 - ; |
Bài 2. (1,5 điểm) Thực hiện phép tính:
|
a) ;
|
b) ;
|
c) .
|
Bài 3. (1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một
cửa sổ hình vuông với các kích thước như hình vẽ.
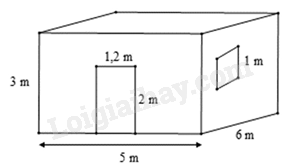
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này
(không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước
thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m.
Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là
1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
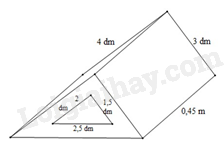
a) Tính thể tích của khối gỗ.
b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:
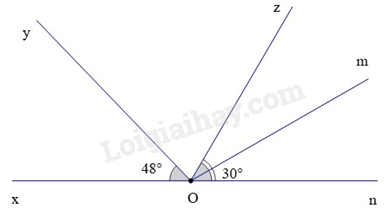
Biết rằng và Om là phân giác của .
a) Kể tên các góc (khác góc bẹt) kề với ; góc kề bù với .
b) Tính số đo của góc .
Bài 6. (0,5 điểm) Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức:
-------- Hết --------
Đáp án
Phần trắc nghiệm (3 điểm)
|
Câu 1: D |
Câu 2: B |
Câu 3: A |
Câu 4: C |
Câu 5: B |
Câu 6: B |
|
Câu 7. A |
Câu 8. B |
Câu 9. C |
Câu 10. A |
Câu 11. B |
Câu 12. D |
Phần tự luận.
Bài 1: (1 điểm).
Lời giải
a.
Vậy .
b. 100 -
=> x + 1 = 10 hoặc x + 1 = -10
hay x = 9 hoặc x = -11.
Vậy x = 9 hoặc x = -11.
Bài 2. (1,5 điểm).
Lời giải
a)
.
b)
.
c)
Bài 3. (1 điểm)
Lời giải
Diện tích xung quanh của căn phòng là: Sxq = 2.(5 + 6).3 = 66(m2).
Diện tích phần cửa lớn và cửa sổ là: 1,2 . 2 + 1 . 1 = 3,4 (m2).
Diện tích phần cần sơn là: 66 – 3,4 = 62,6 (m2)
Tổng chi phí cần để sơn là: 62,6. 30 000 = 1 878 000 (đồng).
Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.
Bài 4. (1,5 điểm)
Lời giải
Đổi: 3 dm = 30 cm; 4 dm = 40 cm; 0,5 m = 50 cm;
1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm; 0,45 m = 45 cm.
a) Thể tích khối gỗ là: (cm3)
b) Diện tích xung quanh của gỗ là: (30 + 40 + 50).45 = 5400(cm2)
Diện tích xung quanh của cái lỗ là: (20 +15 + 25).45 = 2700(cm2)
Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:
(cm2)
Diện tích bề mặt cần sơn là: 5400 + 2700 - 450 = 7650(cm2) = 0,765(m2)
Vậy diện tích cần sơn là 0,765m2.
Bài 5. (1,5 điểm)
Lời giải
a) Các góc (khác góc bẹt) kề với là , , .
Góc kề bù với là .
b) Theo bài ta có Om là tia phân giác của .
Suy ra (tính chất tia phân giác của một góc) (1)
Mà (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Ta có
Hay
Vậy số đo của .
Bài 6. (0,5 điểm).
Lời giải
Ta có nên hay . Dấu “=” xảy ra khi và chỉ khi .
Vậy giá trị nhỏ nhất của M là 7 khi x = 5.