Với giải bài 2 trang 97 Toán lớp 6 Tập 1 Cánh diều chi tiết được biên soạn bám sát nội dung bài học Toán 6 Bài 1: Tam giác đều. Hình vuông. Lục giác đều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải Toán lớp 6 Bài 1: Tam giác đều. Hình vuông. Lục giác đều
Bài 2 trang 97 Toán lớp 6 Tập 1: Một mảnh vườn có dạng hình vuông với chiều dài cạnh bằng 25m. Người ta để một phần của mảnh vườn làm lối đi rộng 2m như Hình 10, phần còn lại để trồng rau.
a) Tính diện tích phần vườn trồng rau.
b) Người ta làm hàng rào xung quanh mảnh vườn trồng rau và ở một góc vườn rau có để cửa ra vào rộng 2m. Tính độ dài của hàng rào đó.
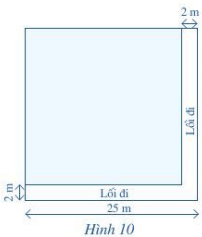
Lời giải:
a) Vì người ta để một phần của mảnh vườn làm lối đi rộng 2 m nên phần vườn trồng rau là mảnh đất hình vuông và có độ dài cạnh là:
25 – 2 = 23 (m)
Diện tích phần vườn trồng rau là:
23 . 23 = 529 (m2)
b) Chu vi của phần vườn trồng rau hình vuông là:
4 . 23 = 92 (m)
Độ dài của hàng rào chính là chu vi của phần vườn trồng rau trừ đi phần cửa ra vào rộng 2 m. Do đó độ dài của hàng rào là:
92 – 2 = 90 (m)
Vậy diện tích của phần vườn trồng rau là 529 m2, độ dài của hàng rào là 90 m.
Bài tập vận dụng:
Bài 1. Một mảnh vườn có dạng hình vuông với chiều dài cạnh bằng 25m. Người ta để một phần của mảnh vườn làm lối đi rộng 2m như Hình dưới, phần còn lại để trồng rau.
a) Tính diện tích phần vườn trồng rau.
b) Người ta làm hàng rào xung quanh mảnh vườn trồng rau và ở một góc vườn rau có để cửa ra vào rộng 2m. Tính độ dài của hàng rào đó.
Lời giải:
a) Vì người ta để một phần của mảnh vườn làm lối đi rộng 2 m nên phần vườn trồng rau là mảnh đất hình vuông và có độ dài cạnh là:
25 – 2 = 23 (m)
Diện tích phần vườn trồng rau là:
23 . 23 = 529 (m2)
b) Chu vi của phần vườn trồng rau hình vuông là:
4 . 23 = 92 (m)
Độ dài của hàng rào chính là chu vi của phần vườn trồng rau trừ đi phần cửa ra vào rộng 2 m. Do đó độ dài của hàng rào là:
92 – 2 = 90 (m)
Vậy diện tích của phần vườn trồng rau là 529 m2, độ dài của hàng rào là 90 m.
Bài 2. Cho lục giác đều ABCDEG.
Các đường chéo chính AD, BE, CG, cắt nhau tại O (Hình dưới).
Vì sao OA = OB = OC = OD = OE = OG?
Lời giải:
Vì ABCDEG là lục giác đều nên:
Các đường chéo chính AD, BE, CG bằng nhau và cắt nhau tạo O, tạo nên các tam giác đều ABO, BCO, CDO, DOE, GOE, AGO.
Lại có trong tam giác đều, ta có ba cạnh bằng nhau, nên
AB = OB = OA
BC = OB = OC
CD = OD = OC
OD = OE = DE
OG = OE = GE
AG = OG = OA
Do đó: OA = OB = OC = OD = OE = OG.
Xem thêm các bài giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Hoạt động 3 trang 94 Toán lớp 6 Tập 1: Vẽ tam giác đều bằng thước và compa khi biết độ dài cạnh...
Hoạt động 5 trang 95 Toán lớp 6 Tập 1: Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh...
Luyện tập 2 trang 95 Toán lớp 6 Tập 1: Vẽ bằng ê ke hình vuông EGHI có độ dài cạnh bằng 6 cm...
Hoạt động 7 trang 96 Toán lớp 6 Tập 1:Quan sát lục giác đều ABCDEG ở Hình 8 ta thấy ...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
