Tài liệu Bộ đề thi Toán lớp 10 học kì 2 có đáp án năm học 2021 - 2022 gồm 14 đề thi tổng hợp từ đề thi môn Toán 10 của các trường THPT trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 2 Toán lớp 10. Mời các bạn cùng đón xem:

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2021 - 2022

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

Phần I: Trắc nghiệm(5,0 điểm)

Câu 1:          Tập nghiệm của bất phương trình \(\frac{3}{{x - 2}} \le \frac{5}{{2x - 1}}\) là:

A. \(\left( { - \infty ;2} \right)\)                   B. \(\left( { - \infty ; - 7} \right] \cup \left( {\frac{1}{2};2} \right)\)                                

C. \(\left( {\frac{1}{2}; + \infty } \right)\)                                     D. \(\left[ { - 7;\frac{1}{2}} \right] \cup \left( {2; + \infty } \right)\)

Câu 2:          Bất phương trình: \[\left| {3x - 1} \right| < 2x + 1\] có nghiệm là:

A. \(( - \frac{1}{2};0)\)                                   B. Vô nghiệm               

C. \[\left( { - \infty ; - \frac{1}{2}} \right) \cup \left( {2; + \infty } \right)\]           D. \[\left( {0;2} \right)\]

Câu 3:          Bất phương trình nào sau đây có tập nghiệm là \(\emptyset \)

A. \( - {x^2} - 8x - 16 \ge 0\)                         B. \({x^2} - 5x + 6 > 0\)     

C. \( - {x^2} - x - 1 > 0\)                                  D. \( - {x^2} + 3x + 2 \ge 0\)

Câu 4:          Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + 1 \ge 2x - 3\\3x + 4 \ge x + 6\end{array} \right.\)

A. \[{\rm{[1}};4]\]     B. \((1;4)\)

C. vô nghiệm                   D. \[{\rm{[}}4; + \infty )\]

Câu 5:          Bất phương trình \({x^2} - 4x + 4 > 0\) có tập nghiệm là:

A. \(\mathbb{R}.\)    B. \(\mathbb{R}\backslash \left\{ 2 \right\}.\)

C. \(\mathbb{R}\backslash \left\{ 0 \right\}.\)                          D. \(\left\{ 2 \right\}.\)

Câu 6:          Giá trị của \(m\) để bất phương trình \[{x^2} + (m + 2)x - m + 1 > 0\] với mọi \(x\) là:

A. \(( - 6;0)\)                B. \[{\rm{[}} - 8;0]\]

C. \(( - 8;0)\)                D. \[\left( {0;8} \right)\]

Câu 7:          Phương trình \[m{x^2} - 2(m - 1)x + m - 5 = 0\] có hai nghiệm phân biệt \[{x_1},{x_2}\] thỏa mãn \[\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} < 3\] khi:

A. \[m \in (\frac{{ - 1}}{3};5) \cup (13; + \infty )\backslash \left\{ 1 \right\}\]

B. \[m \in (\frac{{ - 1}}{3};5) \cup (13; + \infty )\backslash \left\{ 0 \right\}\]

C. \(m \in (5;13)\)

D. \({\rm{m}} \in {\rm{[5;13]}}\)

Câu 8:          Điều kiện xác định của bất phương trình \(\frac{{2x - 3}}{{\sqrt {\left| x \right| + 1} }} > \sqrt {3x} \) là:

A. \(x \ne 0\)               B. \(x > 0\)

C. \(x \ge 0\)               D. \(x \in \mathbb{R}\)

Câu 9:          Cho bảng số liệu ghi lại điểm của \(40\) học sinh trong bài kiểm tra 1 tiết môn toán

Điểm	3	4	5	6	7	8	9	10	Cộng
Số học sinh	2	3	7	18	3	2	4	1	40

Điểm trung bình môn toán của 40 học sinh là?

A. \(6,1\)                      B. \(6,5\)

C. \(6,7\)                      D. \(6,9\)

Câu 10:      Điều tra cân nặng của 30 học sinh lớp 10 (đơn vị: kg) thu được kết quả như sau:

48	50	54	48	54	50	48	54	48	58
45	48	46	48	58	45	55	48	49	48
46	48	52	50	46	48	48	50	46	60

Số học sinh cân nặng \(48kg\) là:

A. \(9\)                          B. \(10\)

C. \(11\)                       D. \(12\)

Câu 11:      Một đường tròn có bán kính \(10cm\). Độ dài cung tròn có số đo bằng \[{30^0}\] là:

A. \[\frac{{45\pi }}{2}\]                                 B. \[\frac{{50\pi }}{3}\]

C. \[\frac{{5\pi }}{3}\]                                   D. \[\frac{\pi }{3}\]

Câu 12:      Giá trị của biểu thức \[\sin {1800^0} + \cos {1620^0} + \tan {945^0} - \sin {1485^0}\] bằng

A. \(\frac{{\sqrt 2 }}{2}\)                              B. \(\sqrt 2 \)

C. \(\frac{{\sqrt 3 }}{2}\)                              D. \( - \frac{1}{{\sqrt 2 }}\)

Câu 13:      Số đo radian của góc \[ - {350^0}\]là:

A. \[\frac{{35\pi }}{{18}}\]                           B. \[ - \frac{{35\pi }}{{18}}\]

C. \[\frac{{18\pi }}{{35}}\]                           D. \[ - \frac{{18\pi }}{{35}}\]

Câu 14:      Cho \(\sin a + \cos a = \frac{5}{4}\). Khi đó \(\sin a.\cos a\) có giá trị bằng:

A. \(\frac{9}{{32}}\)  B. 1

C. \(\frac{3}{{16}}\)  D. \(\frac{5}{4}\)

Câu 15:      Cho \[{\rm{cos}}\alpha  =  - \frac{2}{5}\,\,\,\left( {\pi  < \alpha  < \frac{{3\pi }}{2}} \right)\]. Khi đó \(\frac{1}{2}\) bằng:

A. \( - \frac{{\sqrt {21} }}{2}\)                     B. \(\frac{{\sqrt {21} }}{2}\)

C. \( - \frac{{\sqrt {21} }}{5}\)                     D. \(\frac{{\sqrt {21} }}{3}\)

Câu 16:      Tam giác \(ABC\) với 3 cạnh là \(6;\,\,10;\,\,8\) có diện tích bằng:

A. 21                               B. 24

C. 25                               D. 12

Câu 17:      Trong tam giác \(ABC\)có \(AC = b,AB = c,BC = a\). Chọn kết quả đúng:

A. \(R = \frac{{abc}}{S}\)                               B. \(R = \frac{{4S}}{{abc}}\)

C. \(R = \frac{{4abc}}{S}\)                            D. \(R = \frac{{abc}}{{4S}}\)

Câu 18:      Vectơ pháp tuyến của đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\) và \(B\left( { - 5;6} \right)\) là:

A. \[\overrightarrow n  = (3;2)\]                B. \[\overrightarrow n  = (3; - 2)\]

C. \[\overrightarrow n  = (2; - 3)\]             D. \[\overrightarrow n  = (2;3)\]

Câu 19:      Đường thẳng d có phương trình \[\left\{ \begin{array}{l}x =  - 2 - 5t\\y = 3 + 4t\end{array} \right.\] có một véc tơ chỉ phương là:

A. \[\left( {5; - 4} \right)\]                            B. \[\left( { - 5; - 4} \right)\]

C. \[\left( {4; - 5} \right)\]                            D. \[\left( {4;5} \right)\]

Câu 20 : Phương trình tham số của đường thẳng đi qua \[M( - 3;3)\] và song song với đường thẳng có phương trình \[2x - 5y + 2 = 0\] là:

A. \[\left\{ \begin{array}{l}x = 3 + 5t\\y =  - 3 - 2t\end{array} \right.\]      B. \[\left\{ \begin{array}{l}x =  - 3 + 5t\\y = 3 - 2t\end{array} \right.\]

C. \[\left\{ \begin{array}{l}x =  - 3 - 5t\\y = 3 - 2t\end{array} \right.\]       D. \[\left\{ \begin{array}{l}x = 3 - 5t\\y = 3 - 2t\end{array} \right.\]

Câu 21 : Khoảng cách từ điểm \(M\left( {1; - 1} \right)\) đến đường thẳng r có phương trình \(3x - 4y - 17 = 0\) là:

A. \[\frac{{10}}{{\sqrt 5 }}\]                         B. \[ - \frac{{18}}{5}\]

C. \[\frac{2}{5}\]       D. \(2\)

Câu 20:      Đường tròn \(\left( C \right)\) có tâm \(I\left( { - 2;1} \right)\), bán kính \(R = \sqrt 3 \) có phương trình là:

A. \[{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 3\]       

B. \[{\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 3\]

C. \[{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \sqrt 3 \]

D. \[{\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = \sqrt 3 \]

Câu 21:      Phương trình nào sau đây là phương trình đường tròn?

A. \[{x^2} + {y^2} - 3x + 4y - 1 = 0\]

B. \[{x^2} + {y^2} - 3x + 4y + 7 = 0\]

C. \[{x^2} + {y^2} - x + 2y + 2 = 0\]

D. \[{x^2} + {y^2} + 2y + 2 = 0\]

Câu 22:      Đường thẳng nào sau đây tiếp xúc với đường tròn có phương trình \[{\left( {x - 3} \right)^2} + {y^2} = 9\]

A. \[3x - 4y - 6 = 0\]   B. \[3x - 4y + 5 = 0\]                                     

C. \[3x + 4y + 6 = 0\] D. \[3x - 4y - 5 = 0\]

Câu 23:      Đường tròn (C): \[{x^2} + {y^2} + 2x - 3y - 2 = 0\]có toạ độ tâm \(I\) là:

A. \[I\left( {\frac{3}{2}; - 1} \right)\]         B. \[I\left( {1; - \frac{3}{2}} \right)\]

C. \[I\left( { - 1; - \frac{3}{2}} \right)\]     D. \[I\left( { - 1;\frac{3}{2}} \right)\]

Phần II: Tự luận(5,0 điểm)

Câu 1(1,5 điểm) Giải các bất phương trình sau:

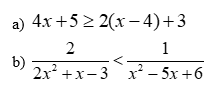
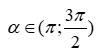Câu 2 (1,0 điểm) Cho  với . Tính các giá trị lượng giác còn lại của cung $\alpha$

Câu 3(1,0 điểm)

a) Cho tam giác ABC biết AB = 3; BC = 8 và $\hat{B}=60°$. Tính độ dài cạnh AC.

b) Tìm m để hệ phương trình sau có nghiệm duy nhất: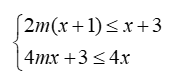 

Câu 4(1,5 điểm) Trong hệ toạ độ Oxy cho tam giác ABC biết A(5; -8), B(-2; -1), C(6; -7)

a) Viết phương trình tham số của mặt thẳng ABC

b) Tìm toạ độ điểm H là hình chiếu của điểm A lên đường thẳng $∆: x-5y+7=0$

c) Viết phương trình đường tròn ngoại tiếp tam giác ABC.

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2021 - 2022

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

I. PHẦN TRẮC NGHIỆM.

Câu 1.      Đường thẳng \[(\Delta )\] đi qua hai điểm, \[A\left( {3; - 2} \right)\]và \[B\left( {5;2} \right)\] là:

A. \[(\Delta )\,:\,\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y =  - 2 + 4t}\end{array}} \right.\].                              B. \[(\Delta )\,:\,\left\{ {\begin{array}{*{20}{c}}{x = 3 - 3t}\\{y =  - 2 - 5t}\end{array}} \right.\].  

C. \[(\Delta )\,:\,\left\{ {\begin{array}{*{20}{c}}{x = 3 + 4t}\\{y = 5 - 2t}\end{array}} \right.\].                       D. \[(\Delta )\,:\,\left\{ {\begin{array}{*{20}{c}}{x =  - 3 + 2t}\\{y =  - 2 + 4t}\end{array}} \right.\].

Câu 2.      Viết phương trình tổng quát của đường thẳng đi qua điểm O(0; 0) và song song với đường thẳng có phương trình 6x - 4y + 1 = 0.

A. \[4x + 6y = 0\].       B. \[6x - 4y = 0\].     

C. \[3x - y - 1y = 0\].  D. \[6x - 4y - 1y = 0\].

Câu 3.      Cho \[\Delta ABC\] có AB=6, AC=8, \[\hat A = {120^{}}\].Độ dài cạnh BC là

A. \[BC \approx 7,2\].                                    B. \[BC \approx 10,7\].    

C. \[BC \approx 12,16\].                               D. \[BC \approx 16,16\].

Câu 4.      Đường tròn \[{x^2} + {y^2} + 2x - 8y - 1 = 0\] có tâm là

A. (-1;-4).                       B. (2; -8).

C. (-1; 4).                        D. (2; - 4).

Câu 5.      Viết phương trình đường tròn biết tâm \[I\left( { - 3;2} \right)\] và bán kính R=2

A. \[{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 4\].

B. \[{\left( {x + 3} \right)^2} - {\left( {y - 2} \right)^2} = 4\].

C. \[{\left( {x + 3} \right)^2} + {\left( {y - 2} \right)^2} = 2\].

D. \[{\left( {x + 3} \right)^2} + {\left( {y - 2} \right)^2} = 4\].

Câu 6.      Tìm Tìm phương trình chính tắc của Elip có trục lớn bằng 12 và trục bé bằng 10

A. \[\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\].                 B. \[\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{81}} = 1\].                   

C. \[\frac{{{x^2}}}{{15}} + \frac{{{y^2}}}{{16}} = 1\].                 D. \[\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{16}} = 1\].

Câu 7.      Tập nghiệm của bất phương trình \[\left( {x - 1} \right)\left( {{x^2} + 3x - 4} \right) \ge 0\] là:

A. \[\left( { - \infty ;1} \right)\].                  B. \[\left( { - 4; + \infty } \right)\].

C. \[\left[ { - 4; + \infty } \right)\].             D. \[\left( { - 4;1} \right)\].

Câu 8.      Bất phương trình \[\frac{{ - {x^2} - 2x + 3}}{{x + 2}}\langle \,0\]có tập nghiệm là

A. \[\left[ { - 3; - 2} \right) \cup \left( {1; + \infty } \right)\].  B. \[\left( { - 3;2} \right)\].                      

C. \[\left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\].     D. \[\left( { - 3; - 2} \right) \cup \left( {1; + \infty } \right)\].

Câu 9.      Phương trình \[{x^2} + \left( {3 - m} \right)x + 1 = 0\]có 2 nghiệm phân biệt khi

A. \[m \in \left( { - \infty ;\left. 1 \right]} \right. \cup \left( {5; + \infty } \right)\].

B. \[m \in \left( { - \infty ;1} \right) \cup \left[ {5; + \infty } \right)\].        

C. \[m \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\].

D. (2; - 4).

Câu 10.    Đường Elip \[\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\] có tiêu cự bằng

A. 1.                                B. 9.

C. 2.                                D. 4.

Câu 11.    Cho \[\cos \alpha  = \frac{{ - 2}}{5}\] \[\left( {\pi \,\langle \,\alpha \,\langle \,\frac{{2\pi }}{3}} \right)\]. Khi đó sin\[\alpha \] bằng

A. \[\frac{{\sqrt {21} }}{5}\].                       B. \[\frac{{ - \sqrt {21} }}{2}\].

C. \[\frac{{ - \sqrt {21} }}{5}\].                    D. \[\frac{{\sqrt {21} }}{3}\].

Câu 12.    Cho tan\[\alpha  =  - 2\] \[\left( {\pi \,\langle \,\alpha \,\langle \,\frac{{2\pi }}{3}} \right)\]. Khi đó cos\[\alpha \] bằng

A. \[\frac{1}{{\sqrt 5 }}\].                             B. \[\frac{{ - 1}}{{\sqrt 5 }}\].

C. \[\frac{1}{{\sqrt 2 }}\].                             D. \[\frac{{ - 1}}{{\sqrt 2 }}\].

Câu 13.    Tính sin \[\left( {\frac{\pi }{3} + x} \right)\]

A. \[\frac{{\sqrt 3 }}{2}\]cos\[x\]+\[\frac{1}{2}\]sin\[x\].        

B. \[\frac{{\sqrt 3 }}{2}\]cos\[x\]-\[\frac{1}{2}\]sin\[x\].

C. \[\frac{1}{2}\]cos\[x\]+\[\frac{{\sqrt 3 }}{2}\]sin\[x\].        

D. \[\frac{1}{2}\]cos\[x\]-\[\frac{{\sqrt 3 }}{2}\]sin\[x\].

Câu 14.    Cho biểu thức \[P = 3{\sin ^2}x + 4{\cos ^2}x\], biết \[\cos x = \frac{1}{2}\]. Giá trị của P bằng

A. \[\frac{7}{4}\].      B. \[\frac{1}{4}\].

C. 7.                                D. \[\frac{{13}}{4}\].

Câu 15.    Nếu \[\sin \alpha  = \frac{{ - 2}}{5}\] thì \[\cos 2\alpha \] có giá trị là

A. \[\frac{{17}}{{25}}\].                                 B. \[\frac{{42}}{{25}}\].

C. \[\frac{{21}}{{25}}\].                                 D. \[\frac{{41}}{{25}}\].

Câu 16.    Rút gọn biểu thức \[\cos \left( {x + \frac{\pi }{4}} \right) - \cos \left( {x - \frac{\pi }{4}} \right)\] ta được

A. \[\sqrt 2 \sin x\].   B. \[ - \sqrt 2 \sin x\].

C. \[\sqrt 2 \cos x\].  D. \[ - \sqrt 2 \cos x\].

Câu 17.    Tính \[\cos 3x\cos x\]

A. \[\frac{1}{2}(\cos 4x + \cos 2x)\].         B. -\[\frac{1}{2}(\cos 4x + \cos 2x)\].

C. \[\frac{1}{2}(\cos 2x + \cos x)\].            D. \[\frac{1}{2}(\cos 2x + \sin x)\].

Câu 18.    Cho phương trình \[{x^2} - 2mx + 5 = 0\] có \[{x_1} = 2\]. Tìm m và nghiệm còn lại

A. \[m = \frac{9}{4}\,\,\,,\,{x_2} = 3\].     B. \[m = \frac{5}{4}\,\,\,,\,{x_2} = 3\].

C. \[m = \frac{9}{4}\,\,\,,\,{x_2} = \frac{1}{2}\].                        D. \[m = \frac{9}{4}\,\,\,,\,{x_2} = \frac{5}{2}\].

Câu 19.    Đẳng thức nào sau đây là đúng

A. \[{\cos ^2}2x = \frac{{1 + \cos 2x}}{2}\].                                 

B. \[{\cos ^2}2x = \frac{{1 - \cos 2x}}{2}\].

C. \[{\cos ^2}2x = \frac{{1 + \cos 4x}}{2}\].                                 

D. \[{\cos ^2}2x = \frac{{1 - \cos 4x}}{2}\].

Câu 20.    Cho bảng phân bố tần số, tìm phương sai

Tuổi	18	19	20	21	22	Cộng
Tần số	10	50	70	29	10	169

A. \[{s^2}_x \approx 0,0092\].                   B. \[{s^2}_x \approx 10,9\].

C. \[{s^2}_x \approx 0,92\].                        D. \[{s^2}_x \approx 12,9\].

Câu 21.    Cho bảng phân bố tần số, tìm độ lệch chuẩn

Tuổi	18	19	20	21	22	Cộng
Tần số	10	50	70	29	10	169

A. \[11,2\].                   B. \[0,96\].

C. \[8,2\].                     D. \[16,3\].

Câu 22.    Đơn giản biểu thức \(C = \cos \left( {\frac{{3\pi }}{2} - a} \right) - \sin \left( {\frac{{3\pi }}{2} - a} \right) + \cos \left( {a - \frac{{7\pi }}{2}} \right) - \sin \left( {a - \frac{{7\pi }}{2}} \right)\)

A. \(\frac{1}{4}\).      B. \( - 2\cos a\).

C. \(2\sin a\).              D. \( - 2\sin a\).

Câu 23.    Đẳng thức nào sau đây là đúng

A. \[\cos 2x = {\sin ^2}x - {\cos ^2}x\].

B. \[\cos 2x = 1 - 2{\cos ^2}x\].

C. \[\cos 2x = 1 - 2{\sin ^2}x\].                  

D. \[\cos 2x = {\sin ^2}x + {\cos ^2}x\].

Câu 24.    Cho \[\Delta ABC\] có AB=6, AC=8, BC=10.Tính \[{S_{\Delta ABC}}\]

A. \[{S_{\Delta ABC}} = 22\].                       B. \[{S_{\Delta ABC}} = 23\].

C. \[{S_{\Delta ABC}} = 24\].                       D. \[{S_{\Delta ABC}} = 25\].

Câu 25.    Tập nghiệm của bất phương trình \[ - {x^2} - 3x + 4 \le 0\]là:

A. \[\left[ { - \infty ; - 4} \right) \cup \left[ {1; + \infty } \right)\].    B. \[\left( { - \infty ; - 4} \right] \cup \left[ {1; + \infty } \right)\].                

C. \[R\,\backslash \left\{ 3 \right\}\].      D. \[\left( { - \infty ; - 4} \right]\]

II. PHẦN TỰ LUẬN.

Câu 1 (1.5 điểm). Giải các bất phương trình sau:

a) \[(3{x^2} - 10x + 3)\left( {4x - 5} \right)\,\, > \,0\]

b) \(\frac{{4 + 3x}}{{{x^2} + x}} \le 0\).

Câu 2 (1 điểm). Cho \[\sin x = \frac{4}{5}\] và \[0 < x < \frac{\pi }{2}\]. Tìm \[\cos 2x\], \(\sin 2x\) và \(\tan \left( {\frac{\pi }{4} - x} \right)\).

Câu 3 (0,5 điểm). Rút gọn biểu thức \[A = \frac{1}{{1 + \tan x}} + \frac{1}{{1 + \cot x}}\].

Câu 4 (0,75 điểm). Viết phương trình đường thẳng đi qua 2 điểm \[A\left( {1;4} \right){\rm{ v\`a  }}B\left( {2;7} \right).\].

Câu 5 (0.75 điểm). Viết phương trình đường tròn \[\left( C \right)\] có tâm \[I(1;2)\] và tiếp xúc với đường thẳng \[(\Delta ):\,3x + 4y - 6 = 0\].

Câu 6 (0,5 điểm). Xác định tiêu cự, độ dài trục lớn, trục bé của elip (E): \[\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\]

 

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Năm học 2021 - 2022

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

Tập nghiệm của bất phương trình \(\frac{{x - 3}}{{2{\rm{x}} - 4}} \le 0\) là.

A. \(\left( { - \infty ;2} \right) \cup \left( {3; + \infty } \right)\)         B. \(\left( { - \infty ;2} \right) \cup \left[ {3; + \infty } \right)\)

C. \(\left( {2;3} \right]\)                                D. \(\left( {2;3} \right)\)

Câu 2:     Phương trình tiếp tuyến tại điểm M(3; 0) với đường tròn (C): \[{x^2} + {y^2} - 4x - 6y + 3 = 0\]là:

A. \(3x + y - 9 = 0\)     B. \(x - 3y - 3 = 0\)

C. \(5{\rm{x}} + 3y - 15 = 0\)                        D. \(x + 3y - 3 = 0\)

Câu 3:     Cho \[\alpha  \in \left( {\pi ;\frac{{3\pi }}{2}} \right)\] và \[tan\alpha  = 2\]. Khi đó \[{\rm{sin}}\alpha \] bằng

A. \[ - \frac{{\sqrt 5 }}{5}\]                          B. \[\frac{{2\sqrt 5 }}{5}\]

C. \[ - \frac{{2\sqrt 5 }}{3}\]                        D. \[ - \frac{{2\sqrt 5 }}{5}\]

Câu 4:     Tìm hai cung lượng giác có cùng tia đầu và cùng tia cuối

A. \(\frac{\pi }{4};\frac{{7\pi }}{4}\)         B. \( - \frac{\pi }{4};\frac{{7\pi }}{2}\)

C. \( - \frac{\pi }{4}; - \frac{{7\pi }}{4}\)  D. \(\frac{\pi }{4}; - \frac{{7\pi }}{4}\)

Câu 5:     Bảng xét dấu của biểu thức nào dưới đây

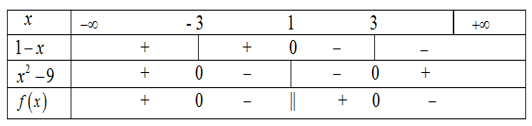
A. \(f\left( x \right) = \frac{{{x^2} - 9}}{{ - x - 1}}\)                     B. \(f\left( x \right) = \frac{{{x^2} - 9}}{{ - x + 1}}\)                       

C. \(f\left( x \right) = \frac{{ - x + 1}}{{{x^2} - 9}}\)                    D. \(f\left( x \right) = \frac{{ - x - 1}}{{{x^2} - 9}}\)

Câu 6: Bảng xét dấu của biểu thức \(y = (x - 1)(2 + 2x)\)là:

 A.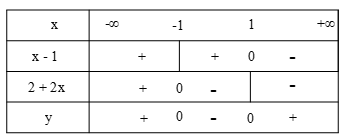 

B.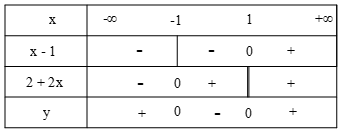 

C.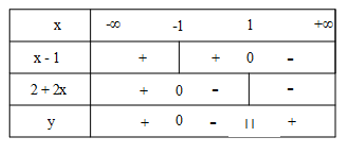 

D.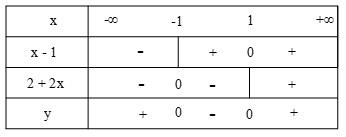

Câu 7:     Nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}15x - 2 > 2x + \frac{1}{3}\\2(x - 4) < \frac{{3x - 14}}{2}\end{array} \right.\) là:

A. \(\frac{7}{{39}} < x < 2\)                           B. \(\frac{7}{{39}} < x < \frac{9}{4}\)

C. \(x < 2\)                   D. \( - 2 < x < 3\)

Câu 8:     Miền KHÔNG tô đen của hình dưới đây là miền nghiệm của bất phương trình nào sau đây?

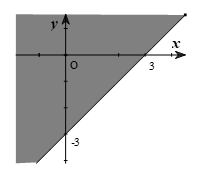
A. \(x + y + 3 > 0\)      B. \(x - y - 3 > 0\)     

C. \(x - y + 3 < 0\)       D. \(x - y - 3 < 0\)

Câu 9:     Góc có số đo \[ - \frac{{3\pi }}{{16}}\] radian được đổi sang độ là:

A. –32⁰55'                       B. –35⁰45'

C. –29⁰30'                       D. –33⁰45'

Câu 10:   Cho tam giác ABC biết \[AB = 28\,cm,AC = 40\,cm,BC = 36\,cm\]. Khẳng định nào SAI?

A. Tam giác ABC có ba góc nhọn

B. Góc lớn nhất là góc B

C. Diện tích tam giác ABC xấp xỉ 2932,5 cm²

D. Góc nhỏ nhất là góc C

Câu 11:   Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn \(\left( C \right):\,{\left( {x + 4} \right)^2} + {\left( {y - 3} \right)^2} = 25\). Tìm phương trình đường thẳng vuông góc với đường thẳng \(\Delta :\,3x - 4y + 10 = 0\) và cắt đường tròn tại 2 điểm A, B, sao cho \(AB = 6\).

A. \[4x + 3y + 13 = 0\,\,;\,\,4x + 3y - 27 = 0\]

B. \[4x + 3y - 13 = 0\,\,;\,\,4x + 3y + 27 = 0\]

C. \[4x + 3y - 1 = 0\,\]                                    

D. \[4x + 3y + 1 = 0\,\]

Câu 12:   Phương trình đường tròn có tâm \(I( - 2;3)\) và bán kính \(R = 4\)là phương trình nào sau đây?

A. \({\left( {x + 2} \right)^2} + {(y - 3)^2} = 16\)

B. \({\left( {x - 2} \right)^2} + {(y - 3)^2} = 16\)                          

C. \({\left( {x - 2} \right)^2} + {(y + 3)^2} = 16\)

D. \({\left( {x + 2} \right)^2} + {(y - 3)^2} = 4\)

Câu 13:   Lập phương trình chính tắc của elip khi có độ dài trục lớn là 6, độ dài tiêu cự là 2.

A. \(\frac{{{x^2}}}{8} + \frac{{{y^2}}}{9} = 1\)

B. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{64}} = 1\)                             

C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)    

D. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\)

Câu 14:   Cho \[\Delta ABC\] có \[A\left( {5;2} \right),B\left( {1;4} \right),C\left( {6; - 1} \right)\]. Phương trình tổng quát của đường trung tuyến CM của \[\Delta ABC\] là.

A. \[4x + 3y - 27 = 0\]                                      B. \[ - 3x + 4y - 12 = 0\]     

C. \[4x + 3y - 21 = 0\]                                      D. \[ - 3x + 4y + 22 = 0\]

Câu 15:   Rút gọn biểu thức \[P = c{\rm{os}}\left( {x + 2017\pi } \right) - 2c{\rm{os}}\left( {x - 2016\pi } \right)\] bằng

A. \[P =  - 3c{\rm{os}}x\]                              B. \[P = 2c{\rm{os}}x\]

C. \[P =  - c{\rm{os}}x\]                                 D. \[P = 0\]

Câu 16:   Tính \[{\rm{sin}}\frac{{25\pi }}{4}\] bằng

A. \( - 0,336\)              B. \[ - \frac{{\sqrt 2 }}{2}\]

C. \(0,336\)                 D. \[\frac{{\sqrt 2 }}{2}\]

Câu 17:   Tập nghiệm của bất phương trình \(x + \sqrt x  > (2\sqrt x  + 3)(\sqrt x  - 1)\) là:

A. \(x < 3\)                   B. \(\left[ \begin{array}{l}x \le 0\\x > 3\end{array} \right.\)

C. \(0 \le x \le 3\)      D. \(0 \le x < 3\)

Câu 18:   Số 2 thuộc tập nghiệm của bất phương trình nào ?

A. \[\left( {2 - x} \right){\left( {x + 2} \right)^2} < 0\]               

B. \[\left( {2x + 1} \right)\left( {1 - x} \right) \ge {x^2}\]

C. \[\frac{1}{{1 - x}} - 2 > 0\]                       

D. \[{\left( {2x + 1} \right)^2} > 1 - x\]

Câu 19:   Cho elip \((E)\)có phương trình chính tắc \[\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\]. Trong các điểm có tọa độ sau đây, điểm nào là tiêu điểm của elip \((E)\)?

A. \[( - 6;0)\]                B. \[(0; - 6)\]

C. \[(10;0)\]                 D. \[( - 36;0)\]

Câu 20:   Cho đường thẳng d đi qua điểm \[Q\left( {5; - 2} \right)\] và vectơ pháp tuyến \(\overrightarrow n  = \left( {3; - 4} \right)\). Hỏi phương trình nào sau đây là phương trình tổng quát của d.

A. \[3x - 4y - 23 = 0\] B. \[4x + 3y - 23 = 0\]                                  

C. \[3x - 4y - 7 = 0\]   D. \[3x - 4y + 23 = 0\]

Câu 21:   Chọn đẳng thức SAI?

A. \(\cot \left( { - \alpha } \right) =  - \cot \alpha \)                  

B. \({\rm{cos}}\left( { - \alpha } \right) =  - {\rm{cos}}\alpha \)

C. \(\tan \left( { - \alpha } \right) =  - \tan \alpha \)                 

D. \(\sin \left( { - \alpha } \right) =  - \sin \alpha \)

Câu 22:   Tìm m để phương trình \({x^2} - 2\left( {m - 1} \right)x + 2{m^2} + 3m - 5 = 0\)có hai nghiệm trái dấu.

A. \(\frac{{ - 5}}{2} < m < 1\)                        B. \[\left[ \begin{array}{l}m < \frac{{ - 5}}{2}\\m > 1\end{array} \right.\]

C. \(\frac{{ - 5}}{2} < m\)                              D. \(m < 1\)

Câu 23:   Cho \[\cos \alpha  =  - \frac{1}{2}\,\,;\,\,\frac{\pi }{2} < \alpha  < \pi \] và \[\sin \beta  = \frac{{\sqrt 3 }}{2}\,\,;\,\,0 < \beta  < \frac{\pi }{2}\]. Hãy tính \[\sin \left( {\alpha  + \beta } \right)\]

A. \( - \frac{1}{2}\)    B. \(\frac{{ - \sqrt 3 }}{4}\)

C. \(0\)                          D. \(\frac{1}{2}\)

Câu 24:   Tính giá trị của biểu thức \[P = (1 - 3\cos 2\alpha )(2 + 3\cos 2\alpha )\] biết \[\sin \alpha  = \frac{2}{3}\]

A. \(P = \frac{{49}}{{27}}\)                           B. \(P = \frac{{20}}{9}\)

C. \(P = \frac{{47}}{{27}}\)                           D. \(P = \frac{{14}}{9}\)

Câu 25:   Cho elip \[(E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\]. Tìm độ dài trục lớn của elip\((E)\).

A. 8                                 B. 6

C. 10                               D. 5

Câu 26:   Kim phút của một đồng hồ BIG BEND ở thành phố London thuộc vương quốc Anh có chiều dài 4,2m. Hỏi trong 15 phút, kim phút vạch trên đường tròn bao nhiêu mét?

A. Xấp xỉ 6,6m                B. Xấp xỉ 4,6m            

C. Xấp xỉ 5,4m                D. Xấp xỉ 2,9m

Câu 27:   Chọn đẳng thức ĐÚNG

A. \[\cot a + \frac{{\sin a}}{{1 + c{\rm{os}}a}} =  - \frac{1}{{\sin a}}\]

B. \[\cot a + \frac{{\sin a}}{{1 + c{\rm{os}}a}} = \frac{1}{{1 + c{\rm{os}}a}}\]

C. \[\cot a + \frac{{\sin a}}{{1 + c{\rm{os}}a}} = \frac{1}{{c{\rm{os}}a}}\]

D. \[c{\rm{ot}}a + \frac{{\sin a}}{{1 + c{\rm{os}}a}} = \frac{1}{{\sin a}}\]

Câu 28:   Cho hai đường thẳng \[{d_1}:2x - 6y + 1 = 0\] và \[{d_2}:x - 2y + 1 = 0\]. Chọn khẳng định ĐÚNG.

A. \[{d_1}\] cắt \[{d_2}\] tại điểm \[A\left( { - 2;\frac{{ - 1}}{2}} \right)\]

B. \[{d_1}\] trùng \[{d_2}\]

C. \[{d_1}\] cắt \[{d_2}\] tại điểm \[B\left( {2;\frac{1}{2}} \right)\]

D. \[{d_1}\] song song \[{d_2}\]

Tự luận

Câu 1: (1điểm) Giải bất phương trình

a)\(\frac{{3 - x}}{{{x^2} + 3{\rm{x}} - 4}} > 0\)                             

b) \(\left| {3x - 2} \right| < 5\)

Câu 2: Cho \(\sin \alpha  = \frac{3}{5}\) và \(0 < \alpha  < \frac{\pi }{2}\). Tính \(\sin 2\alpha \)

Câu 3: Trong cuộc thi pha chế, mỗi đội sử dụng tối đa 210g đường, 9 lít nước, 24g hương liệu và để pha chế nước cam, nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít cam nhận được 60 điểm, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi phải pha chế bao nhiêu lít mỗi loại sao cho điểm thưởng cao nhất?

Câu 4: Viết phương trình đường tròn có tâm \(I\left( { - 1;3} \right)\)và đi qua điểm \(A\left( {2; - 1} \right)\)

Câu 5: Viết phương trình đường thẳng đi qua \(M\left( {1; - 4} \right)\) và vuông góc với đường thẳng d: \(3{\rm{x - 4y + 1 = 0}}\)