Với giải bài 5 trang 42 Toán lớp 6 Tập 1 Cánh diều chi tiết được biên soạn bám sát nội dung bài học Toán 6 Bài 10: Số nguyên tố. Hợp số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải Toán lớp 6 Bài 10: Số nguyên tố. Hợp số
Bài 5 trang 42 Toán lớp 6 Tập 1: Hãy viết ba số:
a) Chỉ có ước nguyên tố là 2.
b) Chỉ có ước nguyên tố là 5
Lời giải:
a) Các số chỉ có ước nguyên tố là 2 là các bội của 2 và không nhận ước nguyên tố nào khác ngoài 2.
Do đó ta có 3 số chỉ có ước nguyên tố là 2 là: 2; 4; 8.
(Ta có thể chứng minh được các số thỏa mãn yêu cầu bài toán có dạng 2n, do đó các em có thể đưa ra bộ ba số tùy ý khác thỏa mãn yêu cầu).
b) Các số chỉ có ước nguyên tố là 5 là các bội của 5 và không nhận ước nguyên tố nào khác ngoài 5.
Do đó ta có 3 số chỉ có ước nguyên tố là 5 là: 5; 25; 125.
(Ta có thể chứng minh được các số thỏa mãn yêu cầu bài toán có dạng 5n, do đó các em có thể đưa ra bộ ba số tùy ý khác thỏa mãn yêu cầu).
Bài tập vận dụng:
Bài 1. Cho các số 36, 37, 69, 75. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Lời giải:
a) Số 37 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và 37.
b) Ta có
+ Số 36 có chữ số tận cùng là 6 nên nó chia hết cho 2.
Do đó số 36 là hợp số vì ngoài hai ước là 1 và 36, nó còn có ít nhất một ước nữa là 2.
+ Số 69 có tổng các chữ số là 6 + 9 = 15 chia hết cho 3 nên số 69 chia hết cho 3.
Do đó số 69 là hợp số vì ngoài hai ước là 1 và 69 thì nó còn có ít nhất một ước nữa là 3.
+ Số 75 có chữ số tận cùng là 5 nên nó chia hết cho 5.
Do đó 75 là hợp số vì ngoài hai ước là 1 và 75, nó còn có ít nhất một ước nữa là 5.
Bài 2. Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng là 4n ± 1 với n là số tự nhiên bất kì.
Lời giải:
Khi chia một số tự nhiên a lớn hơn 2 cho 4 thì ta được các số dư là 0, 1, 2, 3. Trường hợp các số dư là 0 và 2 thì a là hợp số.
Thật vậy,
+ Với số dư là 0 thì a chia hết cho 4 nên a là hợp số
+ Với số dư là 2, ta có: a = 4n + 2
Vì 4 chia hết cho 2 nên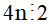 
, 2 chia hết cho 2
Do đó: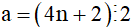 
nên a là hợp số
Ta xét trường hợp số dư là 1 và 3.
+ Với mọi trường hợp số dư là 1 ta có a = 4n + 1
+ Với mọi trường hợp số dư là 3 ta có a = 4n + 3 = 4n + 4 – 1 = 4(n + 1) – 1
Đặt n + 1 = m, khi đó a = 4m – 1
Từ đó suy ra điều phải chứng minh.
Xem thêm các bài giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 41 Toán lớp 6 Tập 1: a) Tìm các ước của mỗi số sau: 2, 3, 4, 5, 6, 7, 17, 34...
Luyện tập 2 trang 42 Toán lớp 6 Tập 1: Tìm các ước nguyên tố của: 23, 24, 26, 27...
Luyện tập 3 trang 42 Toán lớp 6 Tập 1: Viết hai số chỉ có ước nguyên tố là 3...
Bài 2 trang 42 Toán lớp 6 Tập 1: Hãy chỉ ra một số nguyên tố lớn hơn 40 và nhỏ hơn 50...
Bài 4 trang 42 Toán lớp 6 Tập 1: Tìm các ước nguyên tố của: 36, 49, 70...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
