Với giải bài 4 trang 42 Toán lớp 6 Tập 1 Cánh diều chi tiết được biên soạn bám sát nội dung bài học Toán 6 Bài 10: Số nguyên tố. Hợp số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải Toán lớp 6 Bài 10: Số nguyên tố. Hợp số
Bài 4 trang 42 Toán lớp 6 Tập 1: Tìm các ước nguyên tố của: 36, 49, 70.
Lời giải:
Để tìm các ước nguyên tố của một số thì ta tìm các ước của số đó trước, rồi xét xem trong các ước đó, ước nào là số nguyên tố thì số đó được gọi là ước nguyên tố của số đã cho.
+ Để tìm các ước của số 36, ta lấy 36 lần lượt chia cho các số tự nhiên từ 1 đến 36. Các phép chia hết là:
36 : 1 = 36; 36 : 2 = 18; 36 : 3 = 12; 36 : 4 = 9; 36 : 6 = 6; 36 : 9 = 4; 36 : 12 = 3; 36 : 18 = 2; 36 : 36 = 1
Do đó các ước của số 36 là: 1; 2; 3; 4; 6; 9; 12; 18; 36, trong đó có số 2; 3 là các số nguyên tố.
Vậy các ước nguyên tố của 36 là: 2; 3.
+ Để tìm các ước của số 49, ta lấy 49 lần lượt chia cho các số tự nhiên từ 1 đến 49. Các phép chia hết là:
49 : 1= 49; 49 : 7 = 7; 49 : 49 = 1
Do đó các ước của số 49 là: 1; 7; 49, trong đó có số 7 là số nguyên tố.
Vậy ước nguyên tố của 49 là: 7.
+ Để tìm các ước của số 70, ta lấy 70 lần lượt chia cho các số tự nhiên từ 1 đến 70.
Ta tìm được các ước của 70 là: 1; 2; 5; 7; 10; 14; 35; 70, trong đó có các số 2; 5; 7 là các số nguyên tố.
Vậy các ước nguyên tố của 70 là: 2; 5; 7
Bài tập vận dụng:
Bài 1. Cho các số 36, 37, 69, 75. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Lời giải:
a) Số 37 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và 37.
b) Ta có
+ Số 36 có chữ số tận cùng là 6 nên nó chia hết cho 2.
Do đó số 36 là hợp số vì ngoài hai ước là 1 và 36, nó còn có ít nhất một ước nữa là 2.
+ Số 69 có tổng các chữ số là 6 + 9 = 15 chia hết cho 3 nên số 69 chia hết cho 3.
Do đó số 69 là hợp số vì ngoài hai ước là 1 và 69 thì nó còn có ít nhất một ước nữa là 3.
+ Số 75 có chữ số tận cùng là 5 nên nó chia hết cho 5.
Do đó 75 là hợp số vì ngoài hai ước là 1 và 75, nó còn có ít nhất một ước nữa là 5.
Bài 2. Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng là 4n ± 1 với n là số tự nhiên bất kì.
Lời giải:
Khi chia một số tự nhiên a lớn hơn 2 cho 4 thì ta được các số dư là 0, 1, 2, 3. Trường hợp các số dư là 0 và 2 thì a là hợp số.
Thật vậy,
+ Với số dư là 0 thì a chia hết cho 4 nên a là hợp số
+ Với số dư là 2, ta có: a = 4n + 2
Vì 4 chia hết cho 2 nên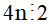 
, 2 chia hết cho 2
Do đó: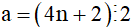 
nên a là hợp số
Ta xét trường hợp số dư là 1 và 3.
+ Với mọi trường hợp số dư là 1 ta có a = 4n + 1
+ Với mọi trường hợp số dư là 3 ta có a = 4n + 3 = 4n + 4 – 1 = 4(n + 1) – 1
Đặt n + 1 = m, khi đó a = 4m – 1
Từ đó suy ra điều phải chứng minh.
Xem thêm các bài giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 41 Toán lớp 6 Tập 1: a) Tìm các ước của mỗi số sau: 2, 3, 4, 5, 6, 7, 17, 34...
Luyện tập 2 trang 42 Toán lớp 6 Tập 1: Tìm các ước nguyên tố của: 23, 24, 26, 27...
Luyện tập 3 trang 42 Toán lớp 6 Tập 1: Viết hai số chỉ có ước nguyên tố là 3...
Bài 2 trang 42 Toán lớp 6 Tập 1: Hãy chỉ ra một số nguyên tố lớn hơn 40 và nhỏ hơn 50...
Bài 5 trang 42 Toán lớp 6 Tập 1: Hãy viết ba số: a) Chỉ có ước nguyên tố là 2...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
