Với giải hoạt động 2 trang 30 Toán lớp 6 Tập 1 Cánh diều chi tiết được biên soạn bám sát nội dung bài học Toán 6 Bài 7: Quan hệ chia hết Tính chất chia hết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải Toán lớp 6 Bài 7: Quan hệ chia hết Tính chất chia hết
Hoạt động 2 trang 31 Toán lớp 6 Tập 1:
a) Thực hiện các phép tính: 9 . 0; 9 . 1; 9 . 2; 9 . 3; 9 . 4; 9 . 5; 9 . 6.
b) Hãy chỉ ra bảy bội của 9.
Lời giải:
a) Ta có: 9 . 0 = 0; 9 . 1 = 9; 9 . 2 = 18; 9 . 3 = 27; 9 . 4 = 36; 9 . 5 = 45; 9 . 6 = 54.
b) Theo câu a, ta thấy các số 0; 9; 18; 27; 36; 45; 54 đều chia hết cho 9 nên bảy bội của 9 là: 0; 9; 18; 27; 36; 45; 54.
Lý thuyết Quan hệ chia hết
1. Khái niệm về chia hết
Cho hai số tự nhiên a và b (b # 0) .
Nếu có số tự nhiên q sao cho a = b . q thì ta nói a chia hết cho b.
Khi a chia hết cho b, ta nói a là bội của b và b là ước của a.
Ví dụ: 42 = 6 . 7 nên 42 chia hết cho 6.
Khi đó ta gọi 42 là bội của 6 và 6 là ước của 42.
Lưu ý:
+ Nếu số dư trong phép chia a cho b bằng 0 thì a chia hết cho b, kí hiệu là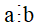 
.
+ Nếu số dư trong phép chia a cho b khác 0 thì a không chia hết cho b, kí hiệu là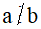 
.
Ví dụ:
+ 4 chia hết cho 2, kí hiệu là
+ 5 không chia hết cho 2, kí hiệu là
Lưu ý: Với a là số tự nhiên khác 0 thì:
+ a là ước của a;
+ a là bội của a;
+ 0 là bội của a;
+ 1 là ước của a.
Ví dụ:
0 và 7 là hai bội của 7.
1 và 12 là hai ước của 12.
2. Cách tìm bội và ước của một số
2.1 Cách tìm bội của một số
Để tìm các bội của n(n∈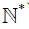
) ta có thể lần lượt nhân n với 0, 1, 2, 3, …. Khi đó, các kết quả nhận được đều là bội của n.
Ví dụ: Tìm các bội nhỏ hơn 20 của 7.
Lời giải:
Để tìm các bội của 7 ta lần lượt nhân 7 với 0, 1, 2, 3,… ta được 0, 7, 14, 21,…
Các bội của 7 là: 0, 7, 14, 21,…
Mà cần tìm các bội của 7 nhỏ hơn 20 nên các số thỏa mãn yêu cầu là 0, 7, 14.
Vậy các bội nhỏ hơn 20 của 7 là 0, 7, 14.
2.2 Cách tìm ước của một số
Để tìm các ước của số tự nhiên n lớn hơn 1 ta có thể lần lượt chia n cho các số tự nhiên từ 1 đến n. Khi đó, các phép chia hết cho ta số chia là ước của n.
Ví dụ: Tìm các ước của 15.
Lời giải:
Thực hiện phép chia số 15 cho lần lượt các số tự nhiên từ 1 đến 15. Các phép chia hết là: 15 : 1 = 15; 15 : 3 = 5; 15 : 5 = 3; 15 : 15 = 1.
Vì vậy, các ước của 15 là 1, 3, 5, 15.
Xem thêm các bài giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
