Với giải bài tập Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5 chi tiết bám sát nội dung sgk Toán 6 Tập 1 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Trả lời câu hỏi giữa bài
Giải Toán 6 trang 35 Tập 1 Cánh diều
a) Lớp nào có thể xếp thành 2 hàng với số lượng học sinh ở mỗi hàng là như nhau?
b) Lớp nào có thể xếp thành 5 hàng với số lượng học sinh ở mỗi hàng là như nhau?
Lời giải:
a) Để biết được lớp nào có thể xếp thành 2 hàng với số lượng học sinh ở mỗi hàng là như nhau thì ta lần lượt lấy số học sinh của mỗi lớp chia cho 2:
40 : 2 = 20; 45 : 2 = 22 (dư 1); 39 : 2 = 19 (dư 1); 44 : 2 = 22; 42 : 2 = 21
Ta thấy 40; 44; 42 chia hết cho 2.
Do đó các lớp 6A, 6D và 6E có thể xếp thành 2 hàng với số lượng học sinh ở mỗi hàng là như nhau.
b) Để biết được lớp nào có thể xếp thành 5 hàng với số lượng học sinh ở mỗi hàng là như nhau thì ta lần lượt lấy số học sinh của mỗi lớp chia cho 5:
40 : 5 = 8; 45 : 5 = 9; 39 : 5 = 7 (dư 4); 44 : 5 = 8 (dư 4); 42 : 5 = 8 (dư 2)
Ta thấy 40; 45 chia hết cho 5.
Do đó các lớp 6A và 6B có thể xếp thành 5 hàng với số lượng học sinh ở mỗi hàng là như nhau.
b) Nêu quan hệ chia hết của các số 10, 22, 54, 76, 98 với số 2.
c) Nêu chữ số tận cùng của các số: 10, 22, 54, 76, 98
Lời giải:
a) Ta có:
10 : 2 = 5; 22 : 2 = 11; 54 : 2 = 27; 76 : 2 = 38; 98 : 2 = 49.
b) Theo câu a, ta thấy các số 10; 22; 54; 76; 98 đều là các số chia hết cho 2.
c) Các chữ số tận cùng của các số 10; 22; 54; 76; 98 lần lượt là 0; 2; 4; 6; 8.
Luyện tập 1 trang 35 Toán lớp 6 Tập 1: Có bao nhiêu số từ 7 210 đến 7 220 chia hết cho 2?
Lời giải:
Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2. Do đó từ số 7 210 đến 7 220 có các số chia hết cho 2 là: 7 210; 7 212; 7 214; 7 216; 7 218; 7 220.
Vậy có 6 số từ 7 210 đến 7 220 chia hết cho 2.
Lời giải:
Vì các số chia hết cho 2 thì có tận cùng là 0; 2; 4; 6; 8 nên trong 3 số đề bài cho là 1; 4; 8 thì ta chọn 4 và 8 làm chữ số tận cùng.
Do đó các số có 2 chữ số khác nhau và chia hết cho 2 được viết từ các chữ số 1, 4, 8 là: 14; 18; 48; 84
Giải Toán 6 trang 36 Tập 1 Cánh diều
Hoạt động 2 trang 36 Toán lớp 6 Tập 1: a) Thực hiện các phép tính: 50 : 5; 65 : 5.
b) Nêu quan hệ chia hết của các số 50; 65 với số 5.
c) Nêu chữ số tận cùng của các số: 50; 65.
Lời giải:
a) Ta có: 50 : 5 = 10; 65 : 5 = 13.
b) Theo câu a, ta thấy các số 50; 65 đều chia hết cho 5.
c) Các chữ số tận cùng của các số 50; 65 lần lượt là 0; 5.
Lời giải:
Ta có:
+ Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
+ Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ta thấy dấu hiệu nhận biết số chia hết cho 2 và 5 đều có chung số có chữ số tận cùng là 0.
Vậy những số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.
Bài tập
Bài 1 trang 36 Toán lớp 6 Tập 1: Cho các số 82, 980, 5 975, 49 173, 756 598. Trong các số đó:
a) Số nào chia hết cho 5, nhưng không chia hết cho 2?
b) Số nào chia hết cho 2, nhưng không chia hết cho 5?
c) Số nào không chia hết cho 2 và không chia hết cho 5?
Lời giải:
a) Số chia hết cho 5 nhưng không chia hết cho 2 có chữ số tận cùng là 5.
Nên trong các số đã cho, số chia hết cho 5 nhưng không chia hết cho 2 là: 5 975.
b) Số chia hết cho 2 nhưng không chia hết cho 5 có chữ số tận cùng là 2; 4; 6; 8.
Nên trong các số đã cho, các số chia hết cho 2 nhưng không chia hết cho 5 là: 82; 756 598.
c) Số không chia hết cho 2 và không chia hết cho 5 thì không có tận cùng là 0; 2; 4; 5; 6; 8, hay nói cách khác là các số có chữ số tận cùng là 1; 3; 7; 9 thì không chia hết cho cả 2 và 5.
Do đó, trong các số đã cho số không chia hết cho 2 và không chia hết cho 5 là: 49 173.
Bài 2 trang 36 Toán lớp 6 Tập 1: Tìm chữ số thích hợp ở dấu * để số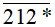 
thỏa mãn mỗi điều kiện sau:
a) Chia hết cho 2;
b) Chia hết cho 5.
c) Chia hết cho cả 2 và 5.
Lời giải:
a) Số chia hết cho 2 là các số có chữ số tận cùng là 0; 2; 4; 6; 8.
Do đó các chữ số thích hợp ở dấu * để số 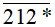chia hết cho 2 là 0; 2; 4; 6; 8.
b) Số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.
Do đó các chữ số thích hợp ở dấu * để số 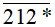chia hết cho 5 là: 0; 5.
c) Số chia hết cho cả 2 và 5 có chữ số tận cùng là 0 (xem Luyện tập 3. Trang 36/SGK).
Do đó các chữ số thích hợp ở dấu * để số 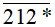chia hết cho cả 2 và 5 là: 0.
a) Các số đó chia hết cho 2;
b) Các số đó chia hết cho 5;
c) Các số đó chia hết cho cả 2 và 5.
Lời giải:
a) Các số cần viết phải có chữ số tận cùng là 0; 2 để thỏa mãn các số đó chia hết cho 2, mà các số đó là các số có hai chữ số khác nhau nên từ các số 0; 2; 5 ta viết được các số thỏa mãn yêu cầu là: 20; 50; 52.
b) Các số cần viết phải có chữ số tận cùng là 0; 5 để thỏa mãn các số đó chia hết cho 5 mà các số đó là các số có hai chữ số khác nhau nên từ các số 0; 2; 5 ta viết được các số thỏa mãn yêu cầu là: 20; 50; 25.
c) Các số cần viết phải có chữ số tận cùng là 0 để thỏa mãn các số đó chia hết cho cả 2 và 5 mà các số đó là các số có hai chữ số khác nhau nên từ các số 0; 2; 5 ta viết được các số thỏa mãn yêu cầu là: 20; 50.
Giải Toán 6 trang 37 Tập 1 Cánh diều
Bài 4 trang 37 Toán lớp 6 Tập 1: Dùng cả ba chữ số 4, 5, 9 để ghép thành số có ba chữ số:
a) Nhỏ nhất và chia hết cho 2;
b) Lớn nhất và chia hết cho 5.
Lời giải:
Vì ta cần dùng cả ba chữ số 4; 5; 9 để ghép thành số có ba chữ số nên mỗi số chỉ được xuất hiện một lần.
a) Ta cần viết số chia hết cho 2 nên số cần viết phải có chữ số tận cùng là 4.
Hai chữ số còn lại là 5 và 9. Để viết được số thỏa mãn yêu cầu số đó là số nhỏ nhất thì chữ số đầu tiên phải là 5.
Do đó từ các chữ số 4; 5; 9 ghép thành số có ba chữ số thỏa mãn số đó là số nhỏ nhất và chia hết cho 2 là 594.
b) Ta cần viết số chia hết cho 5 nên số cần viết phải có chữ số tận cùng là 5.
Hai chữ số còn lại là 4 và 9. Để viết được số thỏa mãn yêu cầu số đó là số lớn nhất thì chữ số đầu tiên phải là 9.
Do đó từ các chữ số 4; 5; 9 ghép thành số có ba chữ số thỏa mãn số đó là số lớn nhất và chia hết cho 5 là 945.
Bài 5 trang 37 Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy giải thích tại sao:
a) A = 61 782 + 94 656 – 76 320 chia hết cho 2;
b) B = 97 485 – 61 820 + 27 465 chia hết cho 5.
Lời giải:
a) Ta có các số 61 782; 94 656; 76 320 là các số có chữ số tận cùng lần lượt là 2; 6; 0 nên theo dấu hiệu chia hết cho 2 thì các số 61 782; 94 656; 76 320 đều là các số chia hết cho 2.
Do đó A = 61 782 + 94 656 – 76 320 là tổng và hiệu của các số chia hết cho 2 nên theo tính chất chia hết của một tổng và một hiệu thì A chia hết cho 2.
b) Ta có các số 97 485; 61 820; 27 465 là các số có chữ số tận cùng lần lượt là 5; 0; 5 nên theo dấu hiệu chia hết cho 5 thì các số 97 485; 61 820; 27 465 đều là các số chia hết cho 5.
Do đó B = 97 485 – 61 820 + 27 465 là tổng và hiệu của các số chia hết cho 5 nên theo tính chất chia hết của một tổng và một hiệu thì B chia hết cho 5.
Lời giải:
Ở tiết mục múa đôi (2 người) của một đội văn nghệ, số người của đội được xếp vừa hết. Do đó số người của đội là số chia hết cho 2.
Đội văn nghệ có khoảng từ 15 người đến 20 người. Từ số 15 đến số 20, ta có các số chia hết cho 2 là: 16; 18; 20.
Do đó số người của đội có thể là 16, 18 hoặc 20 người.
Mà khi hát tốp ca theo nhóm, mỗi nhóm gồm 5 người, đội văn nghệ còn thừa ra 3 người nên số người của đội phải là số chia cho 5 dư 3.
Mà trong các số 16; 18; 20, số chia cho 5 dư 3 là 18.
Vậy đội văn nghệ có 18 người.
Lý thuyết Dấu hiệu chia hết cho 2, cho 5
I. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Ví dụ:
+ Các số 234, 356,... lần lượt có chữ số tận cùng là 4 và 6 nên chúng chia hết cho 2.
+ Các số 1 230, 2 548,... lần lượt có chữ số tận cùng là 0 và 8 nên chúng chia hết cho 2.
II. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ví dụ:
+ Các số 120, 355,... lần lượt có chữ số tận cùng là 0 và 5 nên chúng chia hết cho 5.
+ Các số 1 120, 5 345,... lần lượt có chữ số tận cùng là 0 và 5 nên chúng chia hết cho 5.
Nhận xét: Từ dấu hiệu chia hết cho 2 và 5 ở trên, ta thấy những số chia hết cho cả 2 và 5 là những số có chữ số tận cùng là 0.
Ví dụ: Các số 100, 1 290, … đều chia hết cho cả 2 và 5 và chúng đều có chữ số tận cùng là 0.
Xem thêm các bài giải SGK Toán lớp 6 Cánh diều hay, chi tiết khác:
Bài 7: Quan hệ chia hết. Tính chất chia hết
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
