Với giải bài tập Toán lớp 6 Bài 4. Xác suất thực nghiệm trong một trò chơi và thí nghiệm đơn giản chi tiết bám sát nội dung sgk Toán 6 Tập 2 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6 . Mời các bạn đón xem:
Giải bài tập Bài 4. Xác suất thực nghiệm trong một trò chơi và thí nghiệm đơn giản
Trả lời câu hỏi giữa bài
Giải Toán 6 trang 17 Tập 2 Cánh diều
Xác suất thực nghiệm đề Chỉ gieo được mặt 1 chấm là bao nhiêu?
Lời giải:
Tiến hành gieo xúc xắc, ta thấy:
Khi gieo một con xúc xắc thì các kết quả có thể xảy ra là: xuất hiện mặt 1 chấm, xuất hiện mặt 2 chấm, xuất hiện mặt 3 chấm, xuất hiện mặt 4 chấm, xuất hiện mặt 5 chấm, xuất hiện mặt 6 chấm.
Xác suất thực nghiệm để Chi gieo được mặt 1 chấm trong 6 kết quả có thể xảy ra là: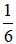 
.
Tung một đồng xu 8 lần liên tiếp, bạn Hoà có kết quả thống kê như sau:
|
Lần tung |
Kết quả tung |
|
1 |
Xuất hiện mặt N |
|
2 |
Xuất hiện mặt N |
|
3 |
Xuất hiện mặt S |
|
4 |
Xuất hiện mặt N |
|
5 |
Xuất hiện mặt S |
|
6 |
Xuất hiện mặt N |
|
7 |
Xuất hiện mặt N |
|
8 |
Xuất hiện mặt S |
a) Hãy kiểm đếm số lần xuất hiện mặt N và số lần xuất hiện mặt S sau 8 lần tung đồng xu.
b) Viết tỉ số của số lần xuất hiện mặt N và tổng số lần tung đồng xu.
c) Viết tỉ số của số lần xuất hiện mặt S và tổng số lần tung đồng xu.
Lời giải:
a) Số lần xuất hiện mặt S: 3 (lần).
Số lần xuất hiện mặt N: 5 (lần).
b) Số lần xuất hiện mặt N là 5, tổng số lần tung đồng xu là 8. Khi đó, tỉ số của số lần xuất hiện mặt N và tổng số lần tung đồng xu là: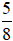 
Vậy tỉ số của số lần xuất hiện mặt N và tổng số lần tung đồng xu là: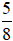
c) Số lần xuất hiện mặt S là 3, tổng số lần tung đồng xu là 8. Khi đó, tỉ số của số lần xuất hiện mặt S và tổng số lần tung đồng xu là: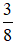
Vậy tỉ số của số lần xuất hiện mặt S và tổng số lần tung đồng xu là: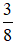
Giải Toán 6 trang 18 Tập 2 Cánh diều
Lời giải:
Số lần xuất hiện mặt S là: 25 – 15 = 10 (lần).
Xác suất thực nghiệm xuất hiện mặt S là: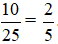 
Vậy xác suất thực nghiệm xuất hiện mặt S là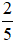 
Mỗi lần bạn Yến lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Sau 10 lần lấy bóng liên tiếp, bạn Yến có kết quả thống kê như sau:
|
Lần lấy bóng |
Kết quả |
|
1 |
Xuất hiện màu xanh |
|
2 |
Xuất hiện màu đỏ |
|
3 |
Xuất hiện màu đỏ |
|
4 |
Xuất hiện màu vàng |
|
5 |
Xuất hiện màu xanh |
|
6 |
Xuất hiện màu vàng |
|
7 |
Xuất hiện màu đỏ |
|
8 |
Xuất hiện màu xanh |
|
9 |
Xuất hiện màu đỏ |
|
10 |
Xuất hiện màu vàng |
a) Hãy kiểm đếm số lần xuất hiện màu xanh, màu đỏ và màu vàng sau 10 lần lấy bóng.
b) Viết tỉ số của số lần xuất hiện màu xanh và tổng số lần lấy bóng.
c) Viết tỉ số của số lần xuất hiện màu đỏ và tổng số lần lấy bóng.
d) Viết tỉ số của số lần xuất hiện màu vàng và tổng số lần lấy bóng.
Lời giải:
a) Sau 10 lần lấy bóng, ta có:
- Số lần xuất hiện màu xanh: 3 (lần);
- Số lần xuất hiện màu đỏ: 4 (lần);
- Số lần xuất hiện màu vàng: 3 (lần);
b) Số lần lấy được bóng màu xanh là 3, tổng số lần lấy ra là 10. Khi đó tỉ số của số lần xuất hiện màu xanh và tổng số lần lấy bóng là: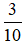 
c) Số lần lấy được bóng màu đỏ là 4, tổng số lần lấy ra là 10. Khi đó tỉ số của số lần xuất hiện màu đỏ và tổng số lần lấy bóng là: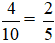 
d) Số lần lấy được bóng màu vàng là 3, tổng số lần lấy ra là 10. Khi đó tỉ số của số lần xuất hiện màu vàng và tổng số lần lấy bóng là: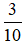
Giải Toán 6 trang 19 Tập 2 Cánh diều
Lời giải:
Xác suất thực nghiệm xuất hiện màu vàng là: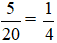
Vậy xác suất thực nghiệm xuất hiện màu vàng là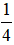 
Bài tập
|
Lần tung |
Kết quả tung |
Số lần xuất hiện mặt N |
Số lần xuất hiện mặt S |
|
1 |
? |
? |
? |
|
… |
? |
Tính xác suất thực nghiệm:
a) Xuất hiện mặt N; b) Xuất hiện mặt S.
Lời giải:
Kết quả thực nghiệm sau khi tung đồng xu 20 lần liên tiếp, ta có bảng sau:
Bảng thống kê kết quả tung đồng xu 20 lần liên tiếp
|
Lần tung |
Kết quả tung |
Số lần xuất hiện mặt N |
Số lần xuất hiện mặt S |
|
1 |
S |
9 |
11 |
|
2 |
S |
||
|
3 |
N |
||
|
4 |
S |
||
|
5 |
S |
||
|
6 |
S |
||
|
7 |
N |
||
|
8 |
N |
||
|
9 |
N |
||
|
10 |
S |
||
|
11 |
S |
||
|
12 |
N |
||
|
13 |
S |
||
|
14 |
N |
||
|
15 |
S |
||
|
16 |
S |
||
|
17 |
N |
||
|
18 |
N |
||
|
19 |
S |
||
|
20 |
N |
a) Xác suất thực nghiệm xuất hiện mặt N là: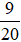 
Vậy xác suất thực nghiệm xuất hiện mặt N là: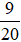
b) Xác suất thực nghiệm xuất hiện mặt S là: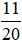 
Vậy xác suất thực nghiệm xuất hiện mặt S là: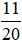
Bài 2 trang 19 Toán lớp 6 Tập 2: Trả lời các câu hỏi sau:
a) Nếu tung một đồng xu 22 lần liên tiếp, có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
b) Nếu tung một đồng xu 25 lần liên tiếp, có 11 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
c) Nếu tung một đồng xu 30 lần liên tiếp, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
Lời giải:
a) Xác suất thực nghiệm xuất hiện mặt N là: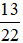
Vậy xác suất thực nghiệm xuất hiện mặt N là: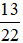
b) Xác suất thực nghiệm xuất hiện mặt S là: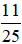
Vậy xác suất thực nghiệm xuất hiện mặt S là: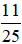
c) Số lần xuất hiện mặt S là: 30 – 14 = 16 (lần).
Xác suất thực nghiệm xuất hiện mặt S là: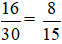 
Giải Toán 6 trang 20 Tập 2 Cánh diều
Rút ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần rút |
Kết quả rút |
Tổng số lần xuất hiện |
|||||||||
|
Số 1 |
Số 2 |
Số 3 |
Số 4 |
Số 5 |
Số 6 |
Số 7 |
Số 8 |
Số 9 |
Số 10 |
||
|
1 |
? |
? |
? |
? |
? |
? |
? |
? |
? |
? |
? |
|
… |
? |
||||||||||
Tính xác suất thực nghiệm:
a) Xuất hiện số l; b) Xuất hiện số 5; c) Xuất hiện số 10.
Lời giải:
Sau 25 lần rút thẻ liên tiếp, ta được kết quả thống kê sau:
|
Lần rút |
Kết quả rút |
Tổng số lần xuất hiện |
|||||||||
|
Số 1 |
Số 2 |
Số 3 |
Số 4 |
Số 5 |
Số 6 |
Số 7 |
Số 8 |
Số 9 |
Số 10 |
||
|
1 |
2 |
1 |
4 |
2 |
2 |
4 |
3 |
3 |
2 |
2 |
2 |
|
2 |
5 |
||||||||||
|
3 |
6 |
||||||||||
|
4 |
10 |
||||||||||
|
5 |
3 |
||||||||||
|
6 |
5 |
||||||||||
|
7 |
7 |
||||||||||
|
8 |
2 |
||||||||||
|
9 |
4 |
||||||||||
|
10 |
4 |
||||||||||
|
11 |
6 |
||||||||||
|
12 |
9 |
||||||||||
|
13 |
5 |
||||||||||
|
14 |
1 |
||||||||||
|
15 |
7 |
||||||||||
|
16 |
8 |
||||||||||
|
17 |
2 |
||||||||||
|
18 |
10 |
||||||||||
|
19 |
2 |
||||||||||
|
20 |
3 |
||||||||||
|
21 |
5 |
||||||||||
|
22 |
8 |
||||||||||
|
23 |
6 |
||||||||||
|
24 |
7 |
||||||||||
|
25 |
9 |
||||||||||
a) Xác suất thực nghiệm xuất hiện số 1 là: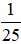
b) Xác suất thực nghiệm xuất hiện số 5 là: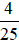
c) Xác suất thực nghiệm xuất hiện số 10 là: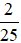 
|
Lần gieo |
Kết quả gieo |
|
1 |
Xuất hiện mặt 2 chấm |
|
2 |
Xuất hiện mặt 1 chấm |
|
3 |
Xuất hiện mặt 6 chấm |
|
4 |
Xuất hiện mặt 4 chấm |
|
5 |
Xuất hiện mặt 4 chấm |
|
6 |
Xuất hiện mặt 5 chấm |
|
7 |
Xuất hiện mặt 3 chấm |
|
8 |
Xuất hiện mặt 5 chấm |
|
9 |
Xuất hiện mặt 1 chấm |
|
10 |
Xuất hiện mặt 1 chấm |
a) Hãy kiểm đếm số lần xuất hiện mặt 1 chấm và số lần xuất hiện mặt 6 chấm sau 10 lần gieo.
b) Tính xác suất thực nghiệm xuất hiện mặt 1 chấm
c) Tính xác suất thực nghiệm xuất hiện mặt 6 chấm.
Lời giải:
a) Sau 10 lần gieo:
Số lần xuất hiện mặt 1 chấm là 3 lần.
Số lần xuất hiện mặt 6 chấm là 1 lần.
b) Xác suất thực nghiệm xuất hiện mặt 1 chấm là: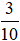
c) Xác suất thực nghiệm xuất hiện mặt 6 chấm là: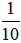 
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?
Lời giải:
a) Xác suất thực nghiệm xuất hiện mặt 2 chấm là: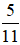
b) Xác suất thực nghiệm xuất hiện mặt 6 chấm là: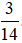 
Xem thêm các bài giải SGK Toán lớp 6 Cánh diều hay, chi tiết khác:
Giải SGK Toán 6 Bài 3: Mô hình xác suất trong một số trò chơi và thí nghiệm đơn giản
Giải SGK Toán 6 Bài ôn tập cuối chương 4
Giải SGK Toán lớp 6 Bài 1: Phân số với tử và mẫu là số nguyên
Giải SGK Toán lớp 6 Bài 2: So sánh các phân số. Hỗn số dương
Lý thuyết Xác suất thực nghiệm trong một trò chơi và thí nghiệm đơn giản
1. Xác suất thực nghiệm trong một số trò chơi tung đồng xu
Xác suất thực nghiệm xuất hiện mặt S khi tung đồng xu nhiều lần bằng:
|
Số lần mặt S xuất hiện |
|
Tổng số lần tung đồng xu |
Xác suất thực nghiệm xuất hiện mặt N khi tung đồng xu nhiều lần bằng:
|
Số lần mặt N xuất hiện |
|
Tổng số lần tung đồng xu |
Chú ý: Xác suất thực nghiệm xuất hiện mặt S (hoặc mặt N) phản ánh số lần xuất hiện mặt đó so với tống số lần tiến hành thực nghiệm.
|
Số lần mặt S xuất hiện |
|
Tổng số lần tung đồng xu |
Ví dụ 1: Tung một đồng xu 50 lần liên tiếp, có 18 lần xuất hiện mặt S.
a) Tính xác suất thực nghiệm xuất hiện mặt S.
b) Tính xác suất thực nghiệm xuất hiện mặt N.
Hướng dẫn giải
a) Xác suất thực nghiệm xuất hiện mặt N là .
b) Khi tung đồng xu 50 lần liên tiếp, do mặt S xuất hiện 18 lần nên mặt N xuất hiện số lần là: 50 – 18 = 32 (lần).
Xác suất thực nghiệm xuất hiện mặt N là: .
2. Xác suất thực nghiệm trong trò chơi lấy vật từ trong hộp
Xác suất thực nghiệm xuất hiện màu A khi lấy bóng nhiều lần bằng:
|
Số lần màu A xuất hiện |
|
Tổng số lần lấy bóng |
Ví dụ 2: Một hộp chứa 5 viên bi, trong đó có 1 viên bi xanh, 1 viên bi đỏ, 1 viên bi vàng, 1 viên bi trắng và 1 viên bi đen. Lấy ngẫu nhiên 1 viên bi. Bạn Tú lấy bi 23 lần liên tiếp thì có 9 lần lấy được viên bi màu đỏ. Tính xác suất thực nghiệm xuất hiện viên bi màu đỏ.
Hướng dẫn giải
Xác suất thực nghiệm xuất hiện viên bi màu đỏ là: .
3. Xác suất thực nghiệm trong trò chơi gieo xúc xắc
Xác suất thực nghiệm xuất hiện mặt k chấm (, 1 ≤ k ≤ 6) khi gieo xúc xắc nhiều lần bằng:
|
Số lần xuất hiện mặt k chấm |
|
Tổng số lần gieo xúc xắc |
Ví dụ 3: Gieo một xúc xắc 6 mặt liên tiếp 20 lần thì thấy 6 lần xuất hiện mặt 1 chấm. Xác suất thực nghiệm xuất hiện mặt 1 chấm bằng bao nhiêu?
Hướng dẫn giải
Xác suất thực nghiệm xuất hiện mặt 1 chấm là: .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
