Với giải luyện 3 trang 7 Toán lớp 6 Tập 1 Cánh diều chi tiết được biên soạn bám sát nội dung bài học Toán 6 Bài 1: Tập hợp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải Toán lớp 6 Bài 1: Tập hợp
Luyện tập 3 trang 7 Toán lớp 6 Tập 1: Cho C = {x | x là số tự nhiên chia cho 3 dư 1, 3 < x < 18}. Hãy viết tập hợp C bằng cách liệt kê các phần tử của tập hợp.
Lời giải:
Ta có: C = {x | x là số tự nhiên chia cho 3 dư 1, 3 < x < 18}
Vì 3 < x < 18 nên x là các số tự nhiên lớn hơn 3 và nhỏ hơn 18.
Lại có các số tự nhiên lớn hơn 3 và nhỏ hơn 18 là: 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17.
Mặt khác x lại là số tự nhiên chia cho 3 dư 1 thỏa mãn lớn hơn 3 và nhỏ hơn 18 nên các số tự nhiên x thỏa mãn yêu cầu là: 4; 7; 10; 13; 16.
Do đó ta viết tập hợp C dưới dạng liệt kê các phần tử như sau:
C = {4; 7; 10; 13; 16}.
Lý thuyết Cách cho tập hợp
Có hai cách cho một tập hợp
4.1 Liệt kê các phần tử của tập hợp.
Ví dụ: Quan sát các số được cho ở hình dưới:

Gọi A là tập hợp các số đó.
Các phần tử của tập hợp A là: 0; 1; 2; 3; 4
Ta viết: A ={0; 1; 2; 3; 4} .
4.2 Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ví dụ:Các phần tử của tập hợp A ở trên đều là các số tự nhiên nhỏ hơn 5. Ta có thể viết:
A = {x| x là số tự nhiên nhỏ hơn 5}.
4.3 Chú ý:
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";".
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
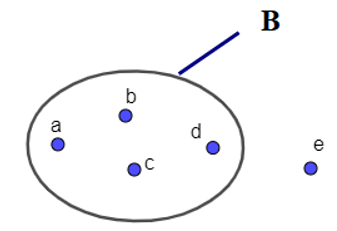
• Ngoài ra ta còn minh họa tập hợp bằng một vòng tròn kín, mỗi phần tử của tập hợp được biểu diễn bằng 1 dấu chấm bên trong vòng tròn kín đó, còn phần tử không thuộc tập hợp được biểu diễn bởi một dấu chấm bên ngoài vòng kín. Cách minh họa tập hợp như trên gọi là biểu đồ Ven (Venn).
Ví dụ: Tập hợp B trong hình vẽ là B = {a; b; c; d}; e ∉ B
Xem thêm các bài giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Hoạt động 2 trang 6, 7 Toán lớp 6 Tập 1 - Cánh diều: Quan sát các số được cho ở Hình 2. ...
Bài 1 trang 7 Toán lớp 6 Tập 1 - Cánh diều: Liệt kê các phần tử của mỗi tập hợp sau: ...