Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 100 bài hình học lớp 9 có hình vẽ phần 2, tài liệu bao gồm 11 trang, tuyển chọn 100 bài hình học lớp 9 có hình vẽ phần 2 (có đáp án và lời giải chi tiết – nếu có), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

100 BÀI HÌNH HỌC LỚP 9 PHẦN 2

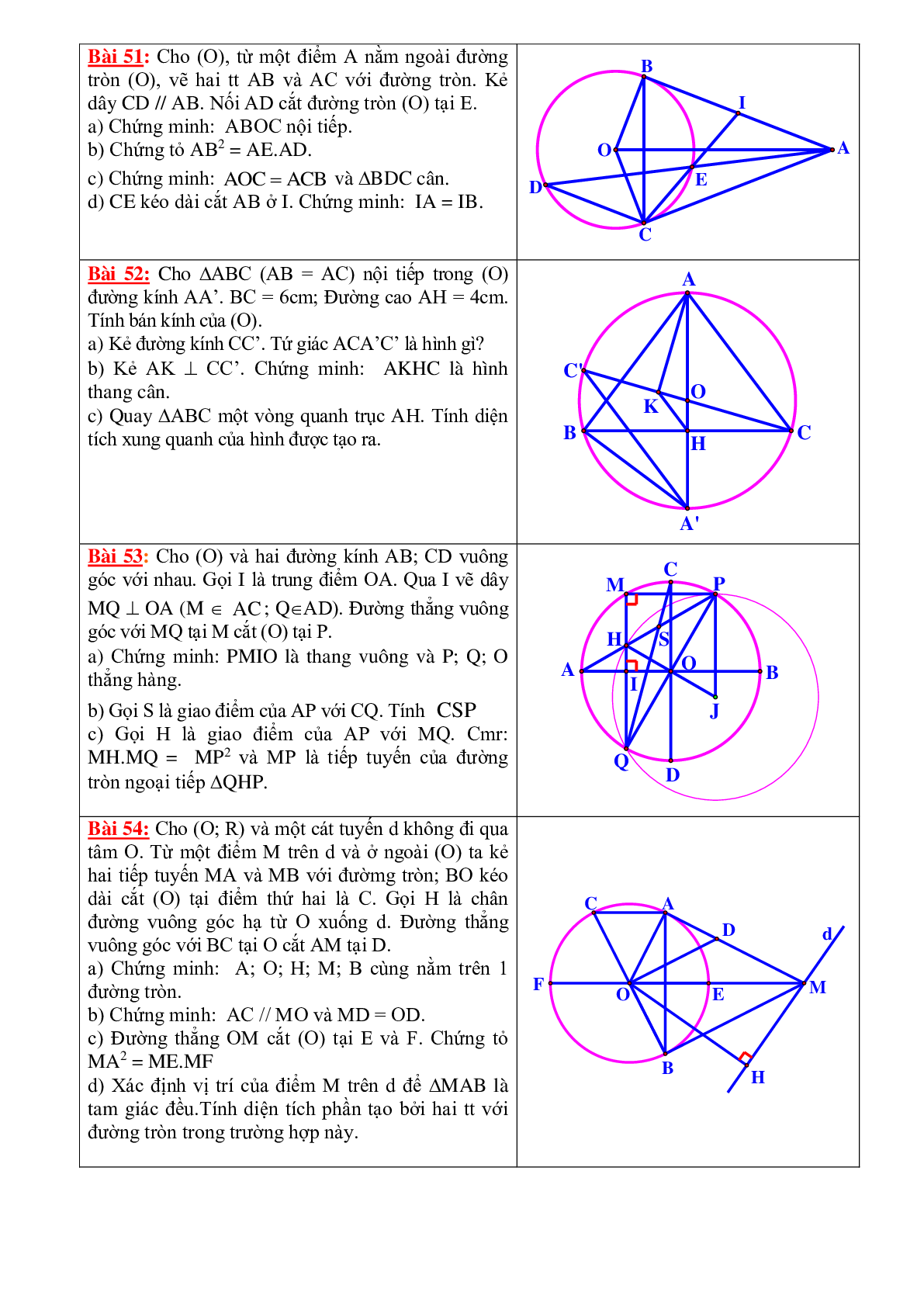
Bài 51: Cho (O), từ một điểm A nằm ngoài đường tròn (O), vẽ hai tt AB và AC với đường tròn. Kẻ dây CD // AB. Nối AD cắt đường tròn (O) tại E.

1. a) Chứng minh: ABOC nội tiếp.
2. b) Chứng tỏ AB² = AE.AD.
3. c) Chứng minh: và DBDC cân.
4. d) CE kéo dài cắt AB ở I. Chứng minh: IA = IB

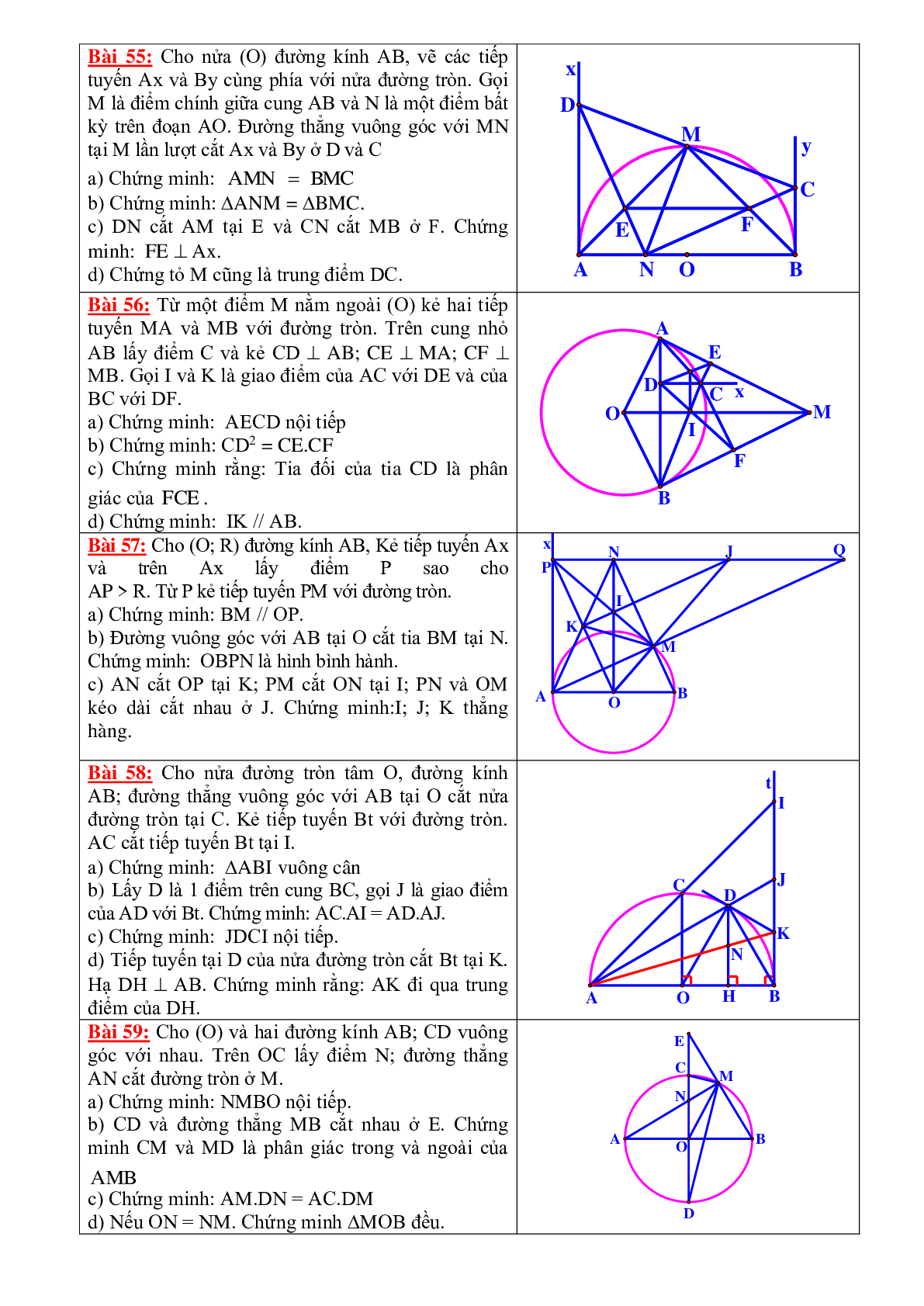
Bài 52: Cho DABC (AB = AC) nội tiếp trong (O) đường kính AA’. BC = 6cm; Đường cao AH = 4cm. Tính bán kính của (O).

a) Kẻ đường kính CC’. Tứ giác ACA’C’ là hình gì?

b) Kẻ AK $\perp$ CC’. Chứng minh: AKHC là hình thang cân.

c) Quay DABC một vòng quanh trục AH. Tính diện tích xung quanh của hình được tạo ra.

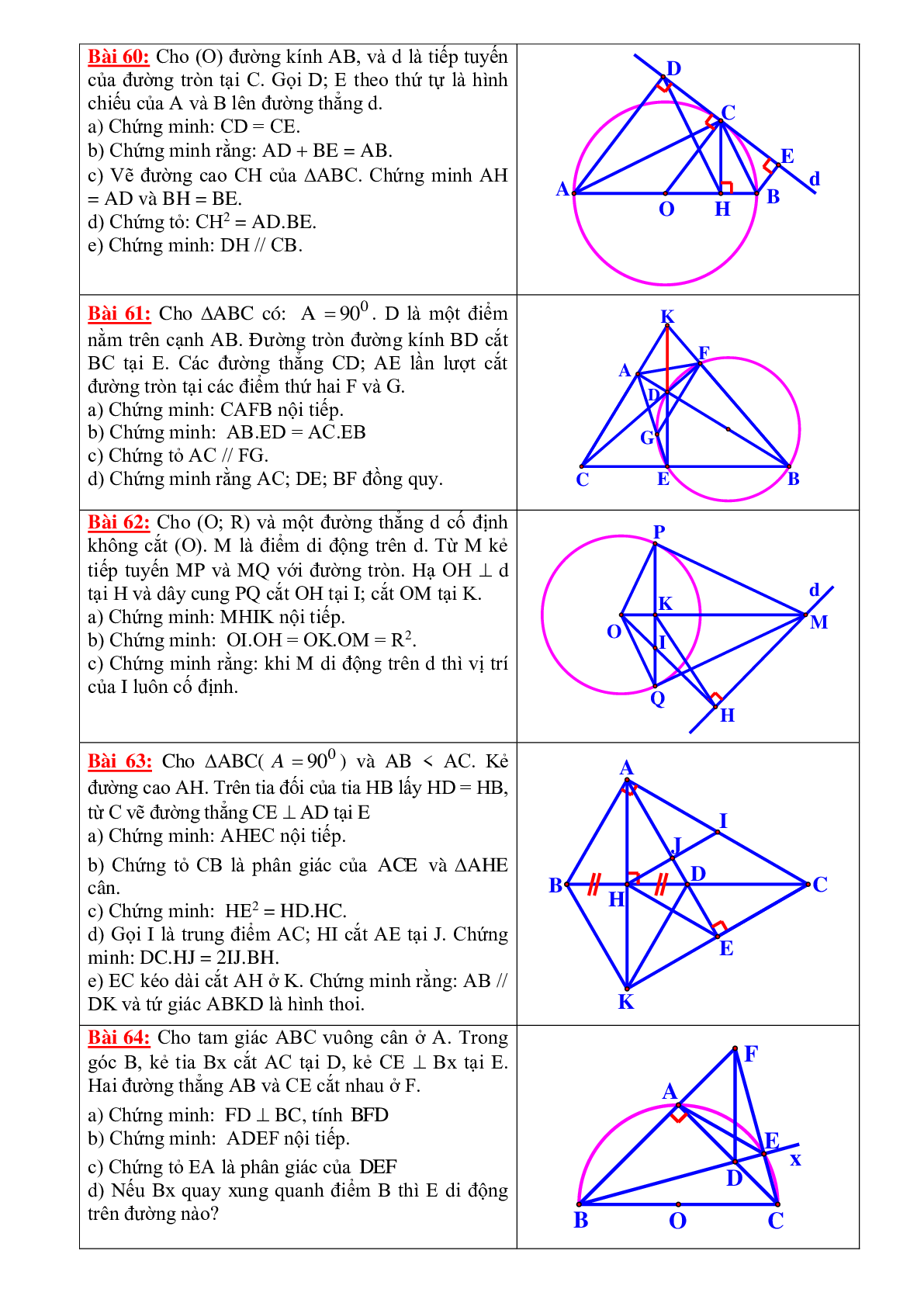
Bài 53: Cho (O) và hai đường kính AB; CD vuông góc với nhau. Gọi I là trung điểm OA. Qua I vẽ dây MQ $\perp$ OA $(M\in \stackrel{⏜}{AC};Q\in AD)$. Đường thẳng vuông góc với MQ tại M cắt (O) tại P.

a) Chứng minh: PMIO là thang vuông và P; Q; O thẳng hàng.

b) Gọi S là giao điểm của AP với CQ. Tính $\widehat{\text{CSP}}$

c) Gọi H là giao điểm của AP với MQ. Cmr: MQ = MP² và MP là tiếp tuyến của đường tròn ngoại tiếp DQHP.

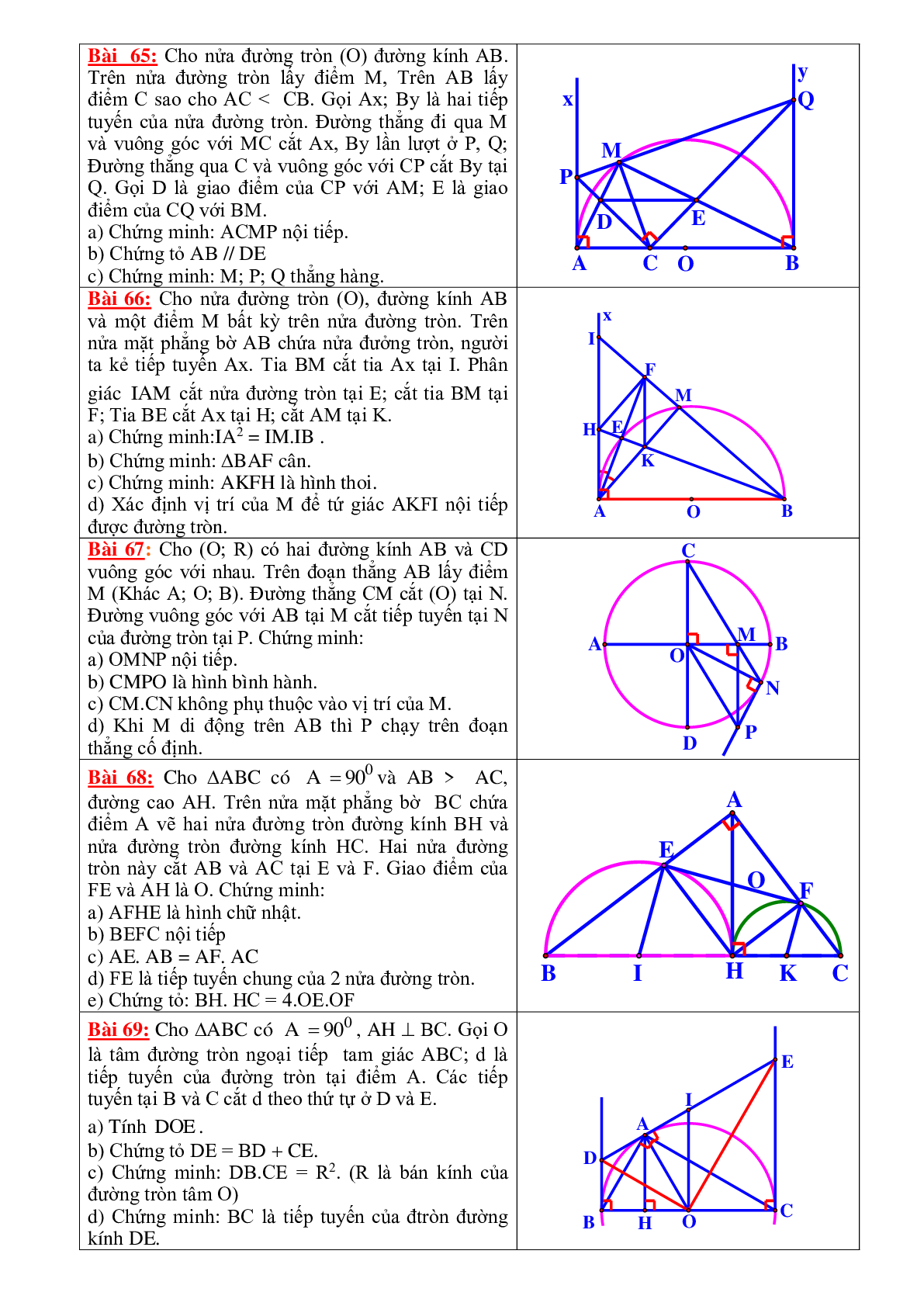
Bài 54: Cho (O; R) và một cát tuyến d không đi qua tâm O. Từ một điểm M trên d và ở ngoài (O) ta kẻ hai tiếp tuyến MA và MB với đườmg tròn; BO kéo dài cắt (O) tại điểm thứ hai là C. Gọi H là chân đường vuông góc hạ từ O xuống d. Đường thẳng vuông góc với BC tại O cắt AM tại D.

a) Chứng minh: A; O; H; M; B cùng nằm trên 1 đường tròn.

b) Chứng minh: AC // MO và MD = OD.

c) Đường thẳng OM cắt (O) tại E và F. Chứng tỏ MA² = ME.MF

d) Xác định vị trí của điểm M trên d để DMAB là tam giác đều.Tính diện tích phần tạo bởi hai tt với đường tròn trong trường hợp này.

Bài 55: Cho nửa (O) đường kính AB, vẽ các tiếp tuyến Ax và By cùng phía với nửa đường tròn. Gọi M là điểm chính giữa cung AB và N là một điểm bất kỳ trên đoạn AO. Đường thẳng vuông góc với MN tại M lần lượt cắt Ax và By ở D và C

a) Chứng minh: $\widehat{\text{AMN}}=\widehat{\text{BMC}}$

b) Chứng minh: $∆ANM = ∆BMC.$

c) DN cắt AM tại E và CN cắt MB ở F. Chứng minh: FE $\perp$Ax

d) Chứng tỏ M cũng là trung điểm DC.

Bài 56: Từ một điểm M nằm ngoài (O) kẻ hai tiếp tuyến MA và MB với đường tròn. Trên cung nhỏ AB lấy điểm C và kẻ CD $\perp$ AB; CE $\perp$ MA; CF $\perp$ MB. Gọi I và K là giao điểm của AC với DE và của BC với DF.

a) Chứng minh: AECD nội tiếp

b) Chứng minh: CD² = CE.CF

c) Chứng minh rằng: Tia đối của tia CD là phân giác của $\widehat{\text{FCE}}$.

d) Chứng minh:  IK // AB.

Bài 57: Cho (O; R) đường kính AB, Kẻ tiếp tuyến Ax và trên Ax lấy điểm P sao cho
AP > R. Từ P kẻ tiếp tuyến PM với đường tròn.

a) Chứng minh: BM // OP.

b) Đường vuông góc với AB tại O cắt tia BM tại N. Chứng minh: OBPN là hình bình hành.

c) AN cắt OP tại K; PM cắt ON tại I; PN và OM kéo dài cắt nhau ở J. Chứng minh:I; J; K thẳng hàng.

Bài 58: Cho nửa đường tròn tâm O, đường kính AB; đường thẳng vuông góc với AB tại O cắt nửa đường tròn tại C. Kẻ tiếp tuyến Bt với đường tròn. AC cắt tiếp tuyến Bt tại I.

a) Chứng minh: DABI vuông cân

b) Lấy D là 1 điểm trên cung BC, gọi J là giao điểm của AD với Bt. Chứng minh: AC.AI = AD.AJ.

c) Chứng minh: JDCI nội tiếp.

d) Tiếp tuyến tại D của nửa đường tròn cắt Bt tại K. Hạ DH $\perp$ AB. Chứng minh rằng: AK đi qua trung điểm của DH.