Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 218 bài toán hàm ẩn hay nhất có giải chi tiết - Toán 12, tài liệu bao gồm 103 trang, tuyển chọn 218 bài tập trắc nghiệm hàm ẩn có đáp án và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

CHỦ ĐỀ I: BIẾT ĐỒ THỊ ĐẠO HÀM CỦA HÀM SỐ.. 3

DẠNG I.1: ĐƠN ĐIỆU.. 3

DẠNG I.2: CỰC TRỊ 22

DẠNG I.3: CỰC TRỊ VÀ ĐỒNG BIẾN.. 37

DẠNG I.4: GTLN – GTNN.. 43

DẠNG I.5: ĐỒ THỊ 50

DẠNG I.6: THAM SỐ 58

CHỦ ĐỀ II: BIẾT ĐỒ THỊ HÀM SỐ f(x) HOẶC BIẾT HÀM SỐ f(x) HOẶC BIẾT BẢNG BIẾN THIÊN.. 60

DẠNG II.1: TIỆM CẬN.. 60

DẠNG II.2: CỰC TRỊ 63

DẠNG II.3: BẢNG BIẾN THIÊN.. 69

DẠNG II.4: TƯƠNG GIAO (chứa tham số) 75

DẠNG II.5: ĐỒ THỊ VÀ THAM SỐ M.. 78

DẠNG II.6: TÌM m  ĐỂ CÓ n  ĐIỂM CỰC TRỊ 86

CHỦ ĐỀ III: BIẾT HÀM SỐ CỦA ĐẠO HÀM.. 94

DẠNG III.1: ĐƠN ĐIỆU.. 94

DẠNG III.2: CỰC TRỊ 96

DẠNG III.3: THAM SỐ m.. 98

HẾT. 102

CHỦ ĐỀ I: BIẾT ĐỒ THỊ ĐẠO HÀM CỦA HÀM SỐ

DẠNG I.1: ĐƠN ĐIỆU

Mức 1: đơn điệu

Câu 1.           Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và \(f'\left( x \right)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?

A. Hàm số đồng biến trên \(\left( {1; + \infty } \right).\)

B. Hàm số đồng biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {3; + \infty } \right).\)

C. Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right).\)

D. Hàm số đồng biến trên \(\left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right).\)

Lời giải

Chọn B Trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {3; + \infty } \right)\)đồ thị hàm số \(f'\left( x \right)\) nằm phía trên trục hoành.

Câu 2.           Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và \(f'\left( x \right)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?

A. Hàm số \(f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right).\)

B. Hàm số \(f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)

C. Hàm số \(f\left( x \right)\) đồng biến trên \(\left( {1; + \infty } \right).\)

D. Hàm số \(f\left( x \right)\) đồng biến trên \(\mathbb{R}.\)

Lời giải

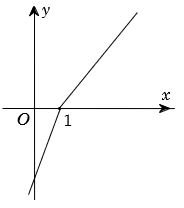
Chọn C Trên khoảng \(\left( {1; + \infty } \right)\)đồ thị hàm số \(f'\left( x \right)\) nằm phía trên trục hoành.

Câu 3.            Cho hàm số \(y = f\left( x \right)\) liên tục và xác định trên \(\mathbb{R}\). Biết \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ, khẳng định nào sau đây đúng?

A. Hàm số \(f\left( x \right)\) đồng biến trên \(\mathbb{R}.\)

B. Hàm số \(f\left( x \right)\) nghịch biến trên \(\mathbb{R}.\)

C. Hàm số \(f\left( x \right)\)chỉ nghịch biến trên khoảng \(\left( {0;1} \right)\).

D. Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\).

Lời giải

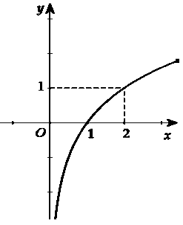
Chọn C Trong khoảng \(\left( {0;1} \right)\) đồ thị hàm số \(y = f'\left( x \right)\)nằm phía dưới trục hoành nên hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( {0;1} \right)\).

Câu 4.           Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị hàm số \(f'\left( x \right)\) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?

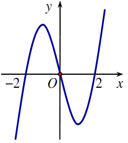
A. Hàm số \(f\left( x \right)\) nghịch biến trên khoảng\[\left( { - 1;1} \right).\]        

B. Hàm số \(f\left( x \right)\) đồng biến trên khoảng \[\left( {1;{\rm{ }}2} \right).\]

C. Hàm số \(f\left( x \right)\) đồng biến trên khoảng \[\left( { - 2;1} \right).\]          

D. Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \[\left( {0;{\rm{ }}2} \right).\]

Lời giải

Chọn D

Cách 1: sử dụng bảng biến thiên. Từ đồ thị của hàm số \(y = f'\left( x \right)\) ta có bảng biến thiên như sau:

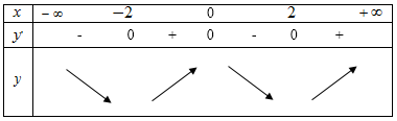Cách 2: Quan sát đồ thị hàm số \(y = f'\left( x \right)\)

Nếu trong khoảng \(K\) đồ thị hàm số \(f'\left( x \right)\) nằm trên trục hoành (có thể tiếp xúc) thì \(f\left( x \right)\) đồng biến trên \(K\).

Nếu trong khoảng \(K\) đồ thị hàm số \(f'\left( x \right)\) nằm dưới trục hoành (có thể tiếp xúc) thì \(f\left( x \right)\) nghịch biến trên \(K\).

Nếu trong khoảng \(K\) đồ thị hàm số \(f'\left( x \right)\) vừa có phần nằm dưới trục hoành vừa có phần nằm trên trục hoành thì loại phương án đó.

Trên khoảng \[\left( {0;{\rm{ }}2} \right)\]ta thấy đồ thị hàm số \(y = f'\left( x \right)\) nằm bên dưới trục hoành.

Câu 5.                  Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị của hàm số \(f'\left( x \right)\) như hình vẽ. Mệnh đề nào sau đây đúng?

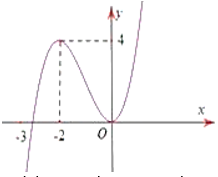
A. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( { - \infty ; - 2} \right);\left( {0; + \infty } \right)\).                                      

B. Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \(\left( { - 2;0} \right).\)

C. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( { - 3; + \infty } \right).\)           

D. Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\)

Lời giải

Chọn C Trên khoảng \(\left( { - 3; + \infty } \right)\) ta thấy đồ thị hàm số \(f'\left( x \right)\) nằm trên trục hoành.

Câu 6.                  Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị của hàm số \(f'\left( x \right)\) như hình vẽ. Mệnh đề nào sau đây đúng?

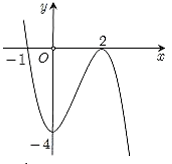
A. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( { - 4;2} \right).\)

B. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( { - \infty ; - 1} \right).\)

C. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( {0;2} \right).\)

D. Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( {2; + \infty } \right).\)

Lời giải

Chọn B Trong khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị hàm số \(f'\left( x \right)\) nằm trên trục hoành nên hàm số đồng biến \(\left( { - \infty ; - 1} \right)\).

Câu 7.           Cho hàm số \[f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\] \[\left( {a \ne 0} \right)\]. Biết rằng hàm số \[f\left( x \right)\] có đạo hàm là \[f'\left( x \right)\] và hàm số \[y = f'\left( x \right)\] có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?

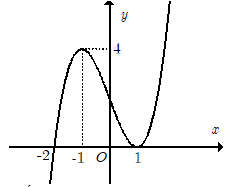
A. Trên \[\left( { - 2;1} \right)\] thì hàm số \[f\left( x \right)\] luôn tăng.         

B. Hàm \[f\left( x \right)\] giảm trên đoạn \[\left[ { - 1;1} \right]\].

C. Hàm \[f\left( x \right)\] đồng biến trên khoảng \[\left( {1; + \infty } \right)\].                                       

D. Hàm\[f\left( x \right)\] nghịch biến trên khoảng \[\left( { - \infty ; - 2} \right)\]

Lời giải

Chọn C Trên khoảng \[\left[ { - 1;1} \right]\]đồ thị hàm số \(f'\left( x \right)\) nằm phía trên trục hoành.

Câu 8.           Cho hàm số \(y = f\left( x \right)\) liên tục và xác định trên \(\mathbb{R}\). Biết \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ, khẳng định nào sau đây đúng?

A. Hàm số \(f\left( x \right)\) đồng biến trên \(\mathbb{R}.\)

B. Hàm số \(f\left( x \right)\) nghịch biến trên \(\mathbb{R}.\)

C. Hàm số \(f\left( x \right)\)chỉ nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).

D. Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).

Lời giải

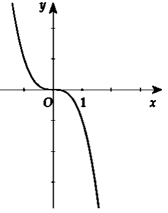
Chọn D Trong khoảng \(\left( {0; + \infty } \right)\) đồ thị hàm số \(y = f'\left( x \right)\)nằm phía dưới trục hoành nên hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) .

Câu 9.           Cho hàm số \(y = f\left( x \right)\) liên tục và xác định trên \(\mathbb{R}\). Biết \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Xét trên \(\left( { - \pi ;\pi } \right)\), khẳng định nào sau đây đúng?

A. Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( { - \pi ;\pi } \right)\).

B. Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { - \pi ;\pi } \right)\).

C. Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { - \pi ;\frac{{ - \pi }}{2}} \right)\) và \(\left( {\frac{\pi }{2};\pi } \right)\).

D. Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0;\pi } \right)\).

Lời giải

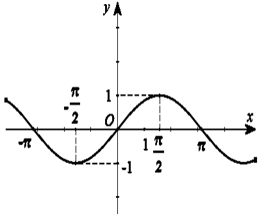
Chọn D Trong khoảng \(\left( {0;\pi } \right)\) đồ thị hàm số \(y = f'\left( x \right)\)nằm phía trên trục hoành nên hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0;\pi } \right)\).

Câu 10.        Cho hàm số \[y = f\left( x \right).\] Đồ thị hàm số \[y = f'\left( x \right)\] như hình bên. Khẳng định nào sau đây sai?

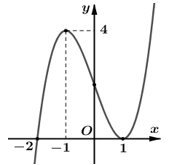
A. Hàm số \[f\left( x \right)\] đồng biến trên \[\left( { - 2;1} \right).\]              

B. Hàm số \[f\left( x \right)\] đồng biến trên \[\left( {1; + \infty } \right)\].

C. Hàm số \[f\left( x \right)\] nghịch biến trên đoạn có độ dài bằng \[2\].       

D. Hàm số \[f\left( x \right)\] nghịch biến trên \[\left( { - \infty ; - 2} \right).\]

Lời giải

Chọn C Dựa vào đồ thị của hàm số \[y = f'\left( x \right)\] ta thấy:

● \[f'\left( x \right) > 0\] khi \[f\left( x \right)\] đồng biến trên các khoảng \[\left( { - 2;1} \right)\], \[\left( {1; + \infty } \right)\]. Suy ra A đúng, B đúng.

● \[f'\left( x \right) < 0\] khi \[f\left( x \right)\] nghịch biến trên khoảng \[\left( { - \infty ; - 2} \right)\]. Suy ra D đúng.

Dùng phương pháp loại trừ, ta chọn C

Mức 2: đơn điệu

Câu 11.        Cho hàm số \[y = f\left( x \right).\] Hàm số \[y = f'(x)\] có đồ thị như hình bên. Hàm số \[y = g\left( x \right) = f(2 - x)\] đồng biến trên khoảng

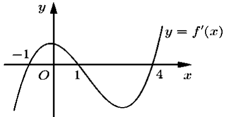
A. \(\left( {1;3} \right)\)    

B. \(\left( {2; + \infty } \right)\)

C. \(\left( { - 2;1} \right)\)                                   

D. \(\left( { - \infty ; - 2} \right)\)

Lời giải

Chọn C Ta có: \(g'\left( x \right) = {\left( {2 - x} \right)^\prime }.f'\left( {2 - x} \right) =  - f'\left( {2 - x} \right)\)

Hàm số đồng biến khi \[g'\left( x \right) > 0 \Leftrightarrow f'\left( {2 - x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}2 - x <  - 1\\1 < 2 - x < 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 3\\ - 2 < x < 1\end{array} \right.\].

Câu 12.        Cho hàm số \[y = f\left( x \right).\] Đồ thị hàm số \[y = f'\left( x \right)\] như hình bên dưới

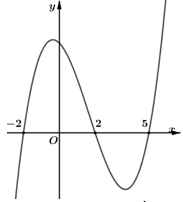
Hàm số \[g\left( x \right) = f\left( {3 - 2x} \right)\] nghịch biến trên khoảng nào trong các khoảng sau?

A. \[\left( {0;2} \right).\]   

B. \[\left( {1;3} \right).\] 

C. \[\left( { - \infty ; - 1} \right).\]                          

D. \[\left( { - 1; + \infty } \right).\]

Lời giải

Chọn C Dựa vào đồ thị, suy ra \[f'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - 2 < x < 2\\x > 5\end{array} \right..\] Ta có \[g'\left( x \right) =  - 2f'\left( {3 - 2x} \right).\]

Xét \[g'\left( x \right) < 0 \Leftrightarrow f'\left( {3 - 2x} \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - 2 < 3 - 2x < 2\\3 - 2x > 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\frac{1}{2} < x < \frac{5}{2}\\x <  - 1\end{array} \right..\]

Vậy \[g\left( x \right)\] nghịch biến trên các khoảng \[\left( {\frac{1}{2};\frac{5}{2}} \right)\] và \[\left( { - \infty ; - 1} \right).\]

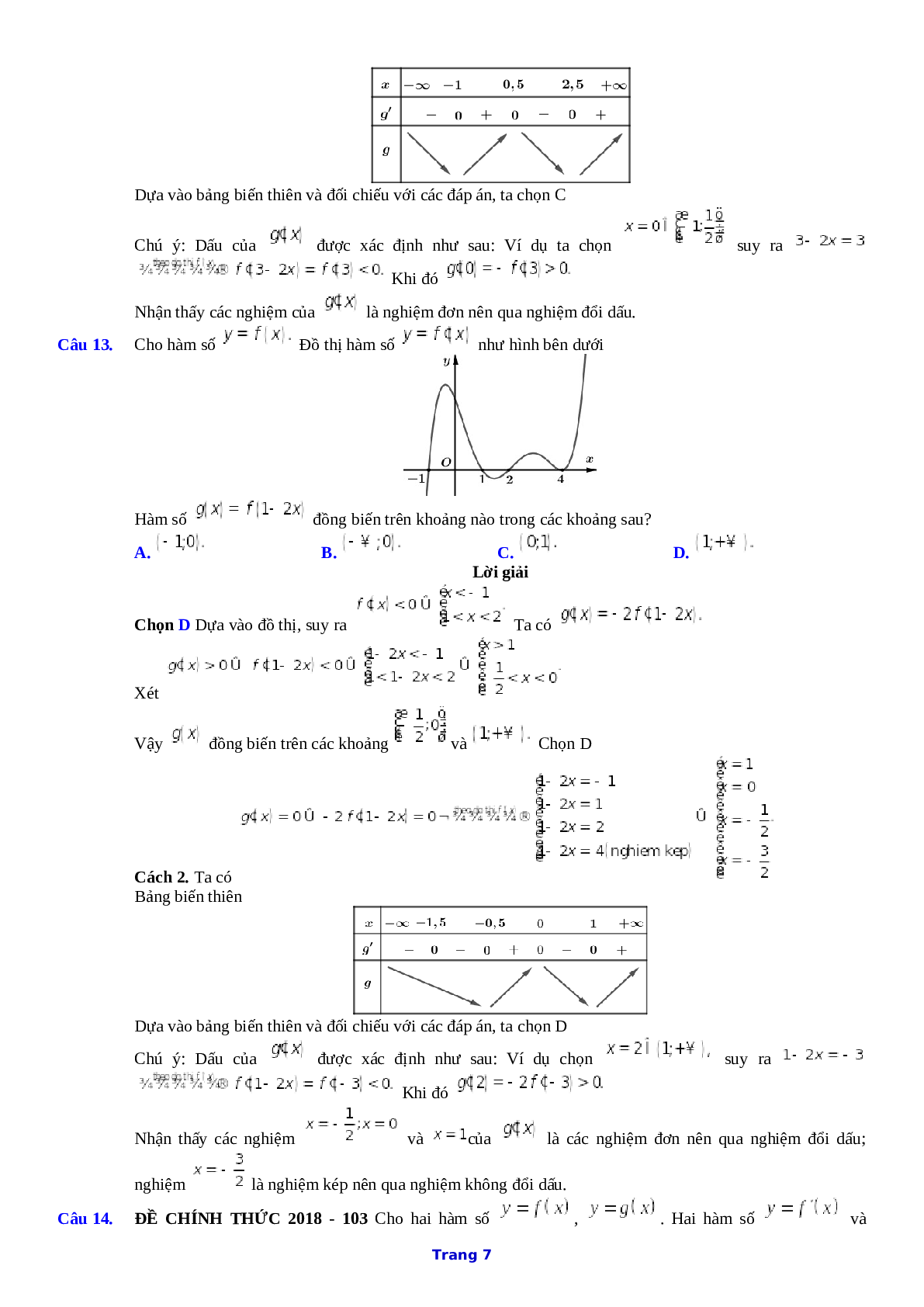
Cách 2. Ta có  Bảng biến thiên

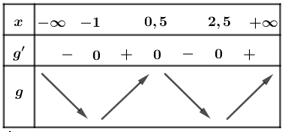
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn C

Chú ý: Dấu của \(g'\left( x \right)\) được xác định như sau: Ví dụ ta chọn \(x = 0 \in \left( { - 1;\frac{1}{2}} \right),\) suy ra \(3 - 2x = 3\)  Khi đó \(g'\left( 0 \right) =  - f'\left( 3 \right) > 0.\)

Nhận thấy các nghiệm của \[g'\left( x \right)\] là nghiệm đơn nên qua nghiệm đổi dấu.

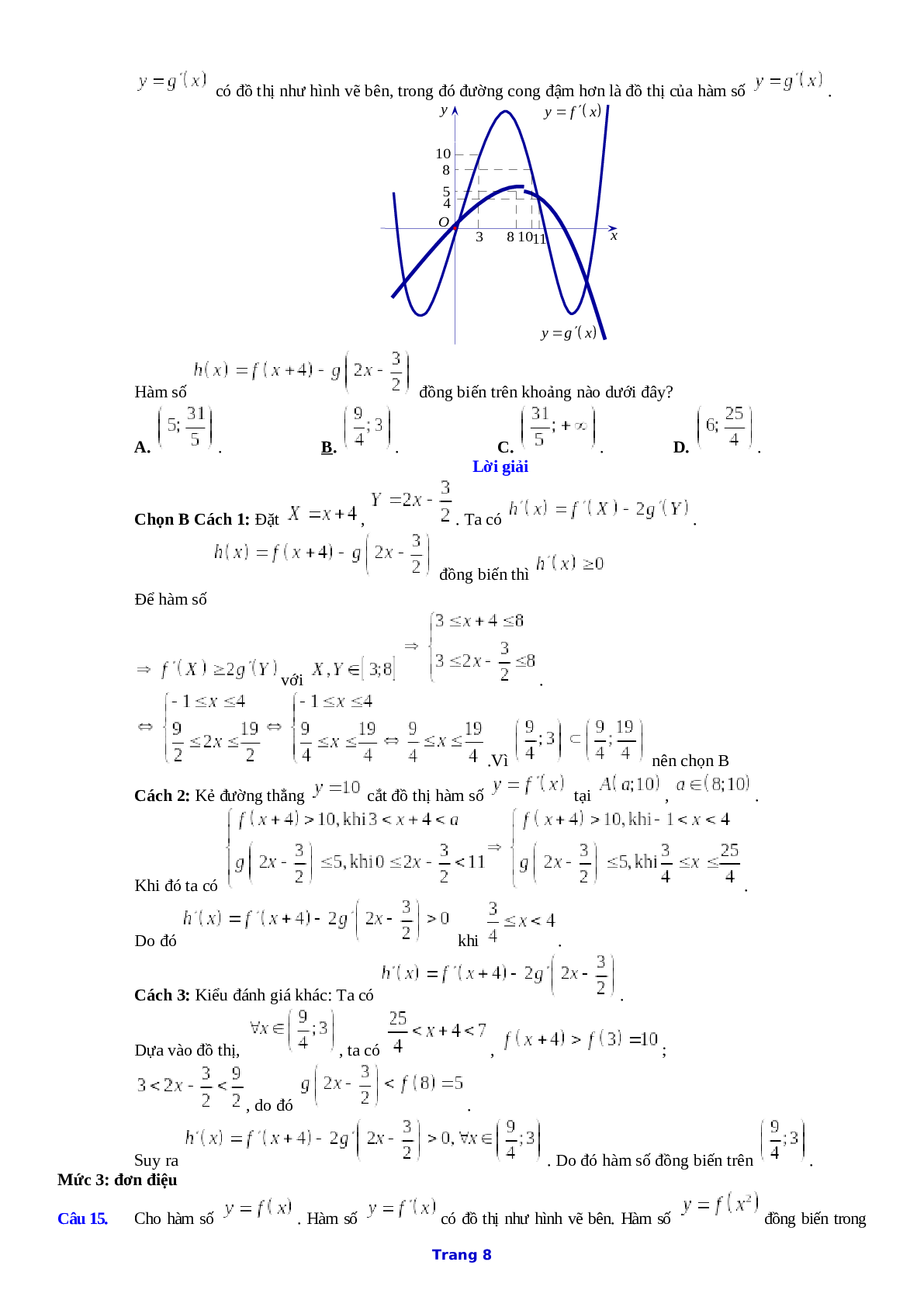
Câu 13.        Cho hàm số \[y = f\left( x \right).\] Đồ thị hàm số \[y = f'\left( x \right)\] như hình bên dưới

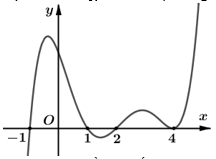
Hàm số \[g\left( x \right) = f\left( {1 - 2x} \right)\] đồng biến trên khoảng nào trong các khoảng sau?

A. \[\left( { - 1;0} \right).\]

B. \[\left( { - \infty ;0} \right).\]                             

C. \[\left( {0;1} \right).\]        

D. \[\left( {1; + \infty } \right).\]

Lời giải

Chọn D Dựa vào đồ thị, suy ra \[f'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x <  - 1\\1 < x < 2\end{array} \right..\] Ta có \[g'\left( x \right) =  - 2f'\left( {1 - 2x} \right).\]

Xét \[g'\left( x \right) > 0 \Leftrightarrow f'\left( {1 - 2x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}1 - 2x <  - 1\\1 < 1 - 2x < 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 1\\ - \frac{1}{2} < x < 0\end{array} \right..\]

Vậy \[g\left( x \right)\] đồng biến trên các khoảng \[\left( { - \frac{1}{2};0} \right)\] và \[\left( {1; + \infty } \right).\] Chọn D

Cách 2. Ta có

Bảng biến thiên

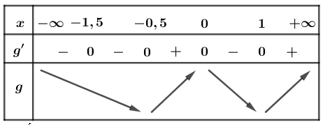
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn D

Chú ý: Dấu của \(g'\left( x \right)\) được xác định như sau: Ví dụ chọn \(x = 2 \in \left( {1; + \infty } \right),\) suy ra \(1 - 2x =  - 3\)  Khi đó \(g'\left( 2 \right) =  - 2f'\left( { - 3} \right) > 0.\)

Nhận thấy các nghiệm \(x =  - \frac{1}{2};x = 0\) và \(x = 1\)của \[g'\left( x \right)\] là các nghiệm đơn nên qua nghiệm đổi dấu; nghiệm \(x =  - \frac{3}{2}\) là nghiệm kép nên qua nghiệm không đổi dấu.

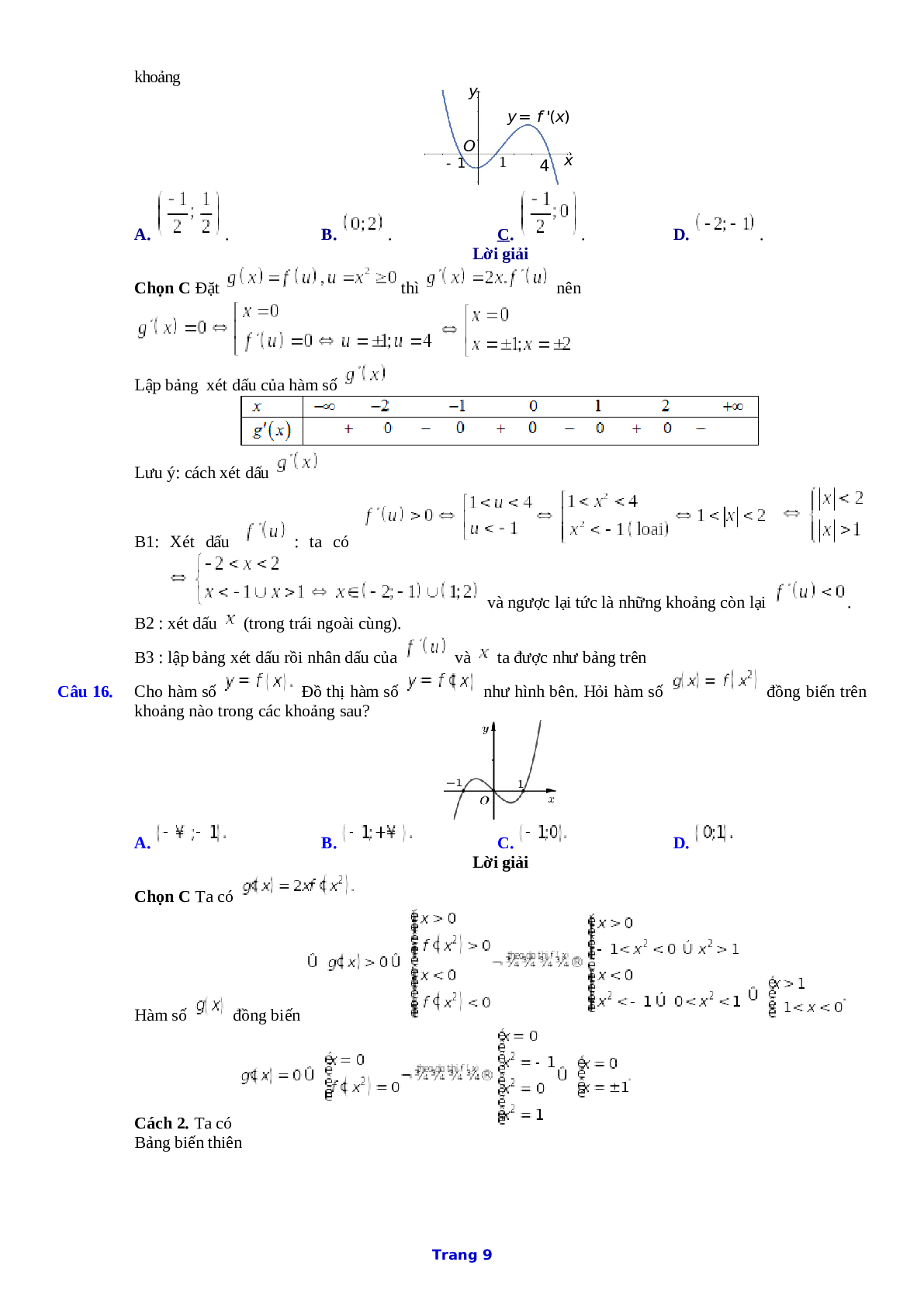
Câu 14.        ĐỀ CHÍNH THỨC 2018 - 103 Cho hai hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\). Hai hàm số \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right)\).

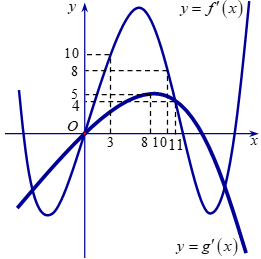
Hàm số \(h\left( x \right) = f\left( {x + 4} \right) - g\left( {2x - \frac{3}{2}} \right)\) đồng biến trên khoảng nào dưới đây?

A. \(\left( {5;\;\frac{{31}}{5}} \right)\).                     

B. \(\left( {\frac{9}{4};\;3} \right)\).                           

C. \(\left( {\frac{{31}}{5};\; + \infty } \right)\).        

D. \(\left( {6;\;\frac{{25}}{4}} \right)\).

Lời giải

Chọn B Cách 1: Đặt \(X = x + 4\), \(Y = 2x - \frac{3}{2}\). Ta có \(h'\left( x \right) = f'\left( X \right) - 2g'\left( Y \right)\).

Để hàm số \(h\left( x \right) = f\left( {x + 4} \right) - g\left( {2x - \frac{3}{2}} \right)\) đồng biến thì \(h'\left( x \right) \ge 0\)

\( \Rightarrow f'\left( X \right) \ge 2g'\left( Y \right)\)với \(X,Y \in \left[ {3;8} \right]\)\( \Rightarrow \left\{ \begin{array}{l}3 \le x + 4 \le 8\\3 \le 2x - \frac{3}{2} \le 8\end{array} \right.\).

\[ \Leftrightarrow \left\{ \begin{array}{l} - 1 \le x \le 4\\\frac{9}{2} \le 2x \le \frac{{19}}{2}\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l} - 1 \le x \le 4\\\frac{9}{4} \le x \le \frac{{19}}{4}\end{array} \right.\]\[ \Leftrightarrow \frac{9}{4} \le x \le \frac{{19}}{4}\].Vì \[\left( {\frac{9}{4};\;3} \right) \subset \left( {\frac{9}{4};\;\frac{{19}}{4}} \right)\] nên chọn B

Cách 2: Kẻ đường thẳng \(y = 10\) cắt đồ thị hàm số \(y = f'\left( x \right)\) tại \(A\left( {a;10} \right)\), \(a \in \left( {8;10} \right)\).

Khi đó ta có \(\left\{ \begin{array}{l}f\left( {x + 4} \right) > 10,khi\,3 < x + 4 < a\\g\left( {2x - \frac{3}{2}} \right) \le 5,khi\,0 \le 2x - \frac{3}{2} < 11\end{array} \right. \Rightarrow \left\{ \begin{array}{l}f\left( {x + 4} \right) > 10,khi\, - 1 < x < 4\\g\left( {2x - \frac{3}{2}} \right) \le 5,khi\,\frac{3}{4} \le x \le \frac{{25}}{4}\end{array} \right.\).

Do đó \(h'\left( x \right) = f'\left( {x + 4} \right) - 2g'\left( {2x - \frac{3}{2}} \right) > 0\) khi \(\frac{3}{4} \le x < 4\).

Cách 3: Kiểu đánh giá khác: Ta có \(h'\left( x \right) = f'\left( {x + 4} \right) - 2g'\left( {2x - \frac{3}{2}} \right)\).

Dựa vào đồ thị, \(\forall x \in \left( {\frac{9}{4};3} \right)\), ta có \(\frac{{25}}{4} < x + 4 < 7\), \(f\left( {x + 4} \right) > f\left( 3 \right) = 10\);

\(3 < 2x - \frac{3}{2} < \frac{9}{2}\), do đó \(g\left( {2x - \frac{3}{2}} \right) < f\left( 8 \right) = 5\).

Suy ra \(h'\left( x \right) = f'\left( {x + 4} \right) - 2g'\left( {2x - \frac{3}{2}} \right) > 0,\forall x \in \left( {\frac{9}{4};3} \right)\). Do đó hàm số đồng biến trên \(\left( {\frac{9}{4};3} \right)\).

Mức 3: đơn điệu

Câu 15.               Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình vẽ bên. Hàm số \(y = f\left( {{x^2}} \right)\)đồng biến trong khoảng

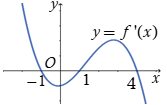
A. \(\left( {\frac{{ - 1}}{2};\,\,\frac{1}{2}} \right)\).    

B. \(\left( {0;\,2} \right)\).                                       

C. \(\left( {\frac{{ - 1}}{2};\,0} \right)\).                  

D. \(\left( { - 2;\, - 1} \right)\).

Lời giải

Chọn C Đặt \(g\left( x \right)\, = \,f\left( u \right),\,u = \,{x^2}\, \ge 0\)thì \[g'\left( x \right) = 2x.f'\left( u \right)\] nên

\[g'\left( x \right) = 0 \Leftrightarrow \,\left[ \begin{array}{l}x = 0\\f'\left( u \right) = 0 \Leftrightarrow u =  \pm 1;\,u = 4\end{array} \right.\] \[ \Leftrightarrow \,\left[ \begin{array}{l}x = 0\\x =  \pm 1;\,x =  \pm 2\end{array} \right.\]

Lập bảng  xét dấu của hàm số \[g'\left( x \right)\]

Lưu ý: cách xét dấu \[g'\left( x \right)\]

B1: Xét dấu \[f'\left( u \right)\] : ta có \[f'\left( u \right) > 0 \Leftrightarrow \left[ \begin{array}{l}1 < u < 4\\u <  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}1 < {x^2} < 4\\{x^2} <  - 1\,\,\left( {{\rm{loai}}} \right)\end{array} \right. \Leftrightarrow 1 < \left| x \right| < 2\] \[ \Leftrightarrow \left\{ \begin{array}{l}\left| x \right| < 2\\\left| x \right| > 1\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l} - 2 < x < 2\\x <  - 1 \cup x > 1\end{array} \right.\]\[ \Leftrightarrow x \in \left( { - 2; - 1} \right) \cup \left( {1;2} \right)\] và ngược lại tức là những khoảng còn lại \[f'\left( u \right) < 0\].

B2 : xét dấu \(x\) (trong trái ngoài cùng).

B3 : lập bảng xét dấu rồi nhân dấu của \[f'\left( u \right)\] và \(x\) ta được như bảng trên

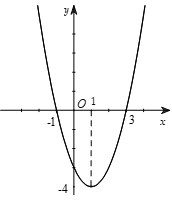
Câu 16.        Cho hàm số \[y = f\left( x \right).\] Đồ thị hàm số \[y = f'\left( x \right)\] như hình bên. Hỏi hàm số \[g\left( x \right) = f\left( {{x^2}} \right)\] đồng biến trên khoảng nào trong các khoảng sau?

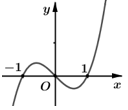
A. \[\left( { - \infty ; - 1} \right).\]                            

B. \[\left( { - 1; + \infty } \right).\]                          

C. \[\left( { - 1;0} \right).\]                                    

D. \[\left( {0;1} \right).\]

Lời giải

Chọn C Ta có \[g'\left( x \right) = 2xf'\left( {{x^2}} \right).\]

Hàm số \(g\left( x \right)\) đồng biến  \( \Leftrightarrow \left[ \begin{array}{l}x > 1\\ - 1 < x < 0\end{array} \right..\)

Cách 2. Ta có

Bảng biến thiên

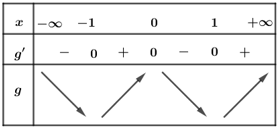
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn C

Chú ý: Dấu của \(g'\left( x \right)\) được xác định như sau: Ví dụ xét trên khoảng \(\left( {1; + \infty } \right)\)

= \(x \in \left( {1; + \infty } \right) \to x > 0.\) \(\left( 1 \right)\)

= \(x \in \left( {1; + \infty } \right) \to {x^2} > 1\). Với  \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right),\) suy ra \[g'\left( x \right) = 2xf\left( {{x^2}} \right) > 0\] trên khoảng \(\left( {1; + \infty } \right)\) nên \[g'\left( x \right)\] mang dấu \( + \).

Nhận thấy các nghiệm của \[g'\left( x \right)\] là nghiệm bội lẻ nên qua nghiệm đổi dấu.

Câu 17.        Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình vẽ.

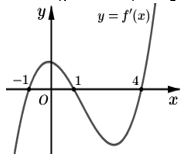
Hàm số \(y = f\left( {{x^2}} \right)\)có bao nhiêu khoảng nghịch biến.

A. \[5\].                           

B. \[3\].                        

C. \[4\].                        

D. \[2\].

Lời giải

Chọn B Ta có \(y' = {\left[ {f\left( {{x^2}} \right)} \right]^\prime } = 2x.f\left( {{x^2}} \right)\)

Hàm số nghịch biến \( \Leftrightarrow y' < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\f'\left( {{x^2}} \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\f'\left( {{x^2}} \right) > 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}1 < x < 2\\x <  - 2 \vee  - 1 < x < 0\end{array} \right.\)

Vậy hàm số \(y = f\left( {{x^2}} \right)\) có 3 khoảng nghịch biến.

Cách 2. Ta có

Bảng biến thiên

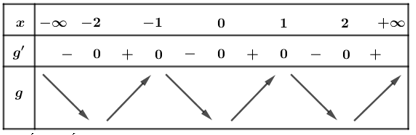
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn B

Chú ý: Dấu của \(g'\left( x \right)\) được xác định như sau: Ví dụ xét trên khoảng \(\left( {2; + \infty } \right)\)

=  \(x \in \left( {2; + \infty } \right) \to x > 0.\)                                                         \(\left( 1 \right)\)

=  \(x \in \left( {2; + \infty } \right) \to {x^2} > 4\). Với             \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right),\) suy ra \[g'\left( x \right) = 2xf\left( {{x^2}} \right) > 0\] trên khoảng \(\left( {2; + \infty } \right)\) nên \[g'\left( x \right)\] mang dấu \( + \).

Nhận thấy các nghiệm của \[g'\left( x \right)\] là nghiệm đơn nên qua nghiệm đổi dấu.

Câu 18.        Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\), đồ thị hình bên là đồ thị của hàm số \(y = f'\left( x \right)\). Xét hàm số \(g\left( x \right) = f\left( {{x^2} - 2} \right)\). Mệnh đề nào dưới đây sai?

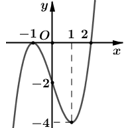
A. Hàm số \(g\left( x \right)\) nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right).\)                                                 

B. Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( {2; + \infty } \right).\)

C. Hàm số \(g\left( x \right)\) nghịch biến trên khoảng \(\left( { - 1;0} \right).\)     

D. Hàm số \(g\left( x \right)\) nghịch biến trên khoảng \(\left( {0;2} \right).\)

Lời giải

Chọn C Ta có: \(g'(x) = 2x.f'\left( {{x^2} - 2} \right)\); \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 2} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 2 =  - 1\\{x^2} - 2 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm 1\\x =  \pm 2\end{array} \right.\)

Từ đồ thị của \(y = f'(x)\) suy ra \(f'({x^2} - 2) > 0 \Leftrightarrow {x^2} - 2 > 2 \Leftrightarrow x \in \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\) và ngược lại.

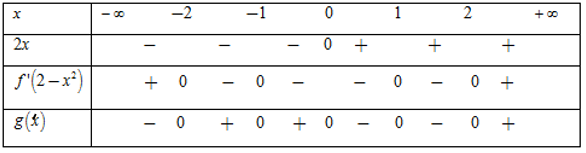
Câu 19.        Cho hàm số \[ - 2.\] Đồ thị hàm số \[y = f'\left( x \right)\] như hình bên dưới

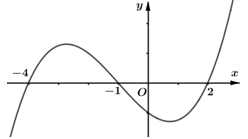
Hỏi hàm số \[g\left( x \right) = f\left( {{x^2} - 5} \right)\] có bao nhiêu khoảng nghịch biến?

A. \[g\left( x \right) = f\left( {{x^2} - 2x + 2} \right)\] 

B. \[3.\]                         

C. \[4.\]                               

D. \[5.\]

Lời giải

Chọn C Ta có \[x \in \mathbb{R}.\]

Bảng biến thiên

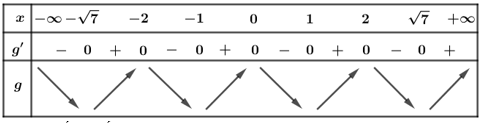
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn C

Câu 20.        Cho hàm số \[y = f\left( x \right).\] Đồ thị hàm số \[y = f'\left( x \right)\] như hình bên. Hỏi hàm số \[g\left( x \right) = f\left( {1 - {x^2}} \right)\] nghịch biến trên khoảng nào trong các khoảng sau?

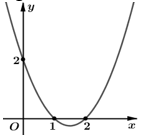
A. \[\left( {1;2} \right)\].   

B. \[\left( {0; + \infty } \right)\].                            

C. \[\left( { - 2; - 1} \right)\].  

D. \[\left( { - 1;1} \right)\].

Lời giải

Chọn B Ta có \[g'\left( x \right) =  - 2xf'\left( {1 - {x^2}} \right).\]Hàm số \(g\left( x \right)\) nghịch biến \( \Leftrightarrow g'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l} - 2x > 0\\f'\left( {1 - {x^2}} \right) < 0\end{array} \right.\\\left\{ \begin{array}{l} - 2x < 0\\f'\left( {1 - {x^2}} \right) > 0\end{array} \right.\end{array} \right..\)

= Trường hợp 1: \(\left\{ \begin{array}{l} - 2x > 0\\f'\left( {1 - {x^2}} \right) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 0\\1 < 1 - {x^2} < 2:{\rm{vo nghiem}}\end{array} \right..\)

= Trường hợp 2: \[\left\{ \begin{array}{l} - 2x < 0\\f'\left( {1 - {x^2}} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\1 - {x^2} < 1 \vee 1 - {x^2} > 2\end{array} \right. \Leftrightarrow x > 0.\] Chọn B

Cách 2. Ta có  Bảng biến thiên

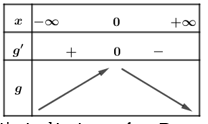
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta chọn B

Chú ý: Dấu của \(g'\left( x \right)\) được xác định như sau: Ví dụ chọn \(x = 1 \in \left( {0; + \infty } \right).\)

=  \(\left( 1 \right)\)

=  \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right),\) suy ra \[g'\left( 1 \right) < 0\] trên khoảng \(\left( {0; + \infty } \right).\)

Nhận thấy nghiệm của \[g'\left( x \right) = 0\] là nghiệm đơn nên qua nghiệm đổi dấu.