Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển tập đề thi vào lớp 10 Môn Toán tỉnh Bình Dương, tài liệu bao gồm 41 trang, tuyển chọn 13 đề thi vào 10 môn Toán. Đề thi được tổng hợp từ các trường trên cả nước giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi Tuyển sinh vào 10 môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Đề thi vào 10 môn Toán tỉnh Bình Dương năm 2020
KỲ THI TUYỂN SINH LỚP 10 THPT
Năm học 2020-2021
Môn thi : TOÁN
Ngày thi : 09/7/2020
Thời gian làm bài : 120 phút (không tính phát đề)
Bài 1. (2 điểm) Giải các phương trình, hệ phương trình sau:
1) 2) 3)
Bài 2. (1,5 điểm)
Cho phương trình : có hai nghiệm phân biệt Không giải phương trình, tính giá trị các
biểu thức sau :
1) 2)
Bài 3. (1,5 điểm)
Cho Parabol (P) và (d) y =
1) Vẽ đồ thị của (P) và ( d) trên cùng một mặt phẳng tọa độ
2) Tìm tọa độ các giao điểm của (P) và (d) bằng phép tính
Bài 4. (1,5 điểm )
Cho biểu thức A =
1) Rút gọn biểu thức A
2) Tính giá trị của biểu thức A khi
Bài 5. (3,5 điểm)
Cho đường tròn ( O;3cm) có đường kính AB và tiếp tuyến Ax. Trên Ax lấy điểm C sao cho AC =8cm, BC cắt đường
tròn (O) tại D. Đường phân giác của góc CAD cắt đường tròn (O) tại M và cắt BC tại N
1) Tính độ dài đoạn thẳng AD
2) Gọi E là giao điểm của AD và MB.Chứng minh tứ giác MNDE nội tiếp được trong đường tròn.
3) Chứng minh tam giác ABN là tam giác cân
4) Kẻ EF vuông góc AB (F ∈ AB).Chứng minh N,E,F thẳng hàng.
Đề thi vào 10 môn Toán tỉnh Bình Dương năm 2023 có lời giải chi tiết
KỲ THI TUYỂN SINH LỚP 10 THPT
Năm học 2020-2021
Môn thi : TOÁN
Ngày thi : 02/6/2023
Thời gian làm bài : 120 phút (không tính phát đề)
Câu 1: Giải các phương trình, hệ phương trình sau:
1)
2) .
3)
Câu 2: Cho Parabol và đường thẳng
1) Vẽ đồ thị của hàm số
2) Viết phương trình đường thẳng biết vuông góc với và tiếp xúc
Câu 3: Cho phương trình (m là tham số).
1) Tìm các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt .
2) Tìm hệ thức liên hệ giữa và mà không phụ thuộc vào tham số m.
Câu 4: Bác Tư đến siêu thị mua một cái quạt máy và một ấm đun siêu tốc với tổng số tiền theo giá niêm yết là 630000 đồng. Tuy nhiên, trong tuần lễ tri ân khách hàng nên siêu thị đã giảm giá quạt máy 15% và giảm giá ấm đun siêu tốc 12% so với giá niêm yết của từng sản phẩm. Nên Bác Tư chỉ phải trả 543000 đồng khi mua 2 sản phẩm trên. Hỏi giá niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc là bao nhiêu?
Câu 5: Cho đường tròn tâm O đường kính AB và một điểm C tùy ý trên (O), (C khác A, B và CA < CB). Các tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại D. Dựng CH vuông góc với BD tại H (H nằm trên BD). Đường thẳng DO cắt CH và CB lần lượt tai M và N.
1) Chứng minh: Tứ giác nội tiếp được trong đường tròn.
2) Chứng minh: .
3) Các đường thẳng và cắt nhau tại . Chứng minh: .
4) Khi quay tam giác DNB một vòng quanh cạnh DN ta được một hình nón. Biết . Tính thể tích của hình nón tạo thành.
----- HẾT -----
Lời giải:
Câu 1 (VD):
Phương pháp:
1)
Bước 1: Tính
Bước 2: So sánh với 0
- phương trình (1) vô nghiệm
- => phương trình (1) có nghiệm kép
- => phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau:
và .
2) Đặt nhân tử chung.
3) Giải hệ bằng phương pháp thế hoặc trừ vế.
Cách giải:
1)
Ta có: nên phương trình có 2 nghiệm phân biệt .
Vậy tập nghiệm của phương trình là .
2) .
ĐKXĐ:
Đặt , phương trình trở thành .
Ta có nên phương trình có hai nghiệm phân biệt
Với .
Vậy tập nghiệm của phương trình là .
3)
Ta có:
.
Vậy hệ phương trình có nghiệm duy nhất (1;2).
Câu 2 (VD):
Cách giải:
Cho Parabol và đường thẳng
1) Vẽ đồ thị của hàm số
Ta có bảng giá trị sau:

Đồ thị hàm số là đường cong parabol đi qua các điểm
Hệ số nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số như sau:
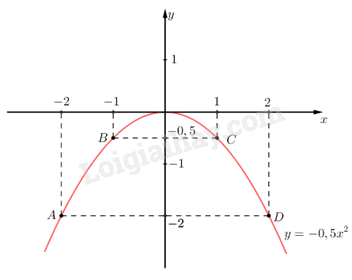
2) Viết phương trình đường thẳng biết vuông góc với và tiếp xúc
Vì vuông góc với nên phương trình đường thẳng có dạng
Để tiếp xúc thì phương trình hoành độ giao điểm có nghiệm duy nhất, tức là:
có nghiệm duy nhất.
hay
Với thì
Vậy phương trình đường thẳng là
Câu 3 (VD):
Phương pháp:
Sử dụng vi ét.
Cách giải:
1) Tìm các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt .
Để phương trình có 2 nghiệm phân biệt thì
Vậy thì phương trình có hai nghiệm phân biệt .
2) Tìm hệ thức liên hệ giữa và mà không phụ thuộc vào tham số m.
Với m > -1, áp dụng hệ thức Vi-ét ta có:
Thay (1) vào (2) ta có:
Vậy hệ thức liên hệ giữa và mà không phụ thuộc vào tham số m là
.
Câu 4 (VD):
Cách giải:
Gọi giá niêm yết của 1 cái quạt máy và 1 ấm siêu tốc lần lượt là (đồng, )
Vì tổng số tiền mua 2 sản phẩm theo giá niêm yết là 630000 đồng nên ta có:
(1)
Tuy nhiên, siêu thị đã giảm giá quạt máy 15% và giảm giá ấm đun siêu tốc 12% so với giá niêm yết của từng sản phẩm.
Do đó:
Số tiền Bác Tư phải trả cho 1 cái quạt máy là: (đồng)
Số tiền Bác Tư phải trả cho 1 ấm siêu tốc là: (đồng)
Do bác Tư phải trả 543000 đồng khi mua 2 sản phẩm nên ta có:
(2)
Từ (1) và (2) ta có hệ phương trình:
Vậy giá niêm yết của 1 cái quạt máy là 380000 đồng, giá niêm yết của 1 ấm siêu tốc là 250000 đồng.
Câu 5 (VD):
Cách giải:
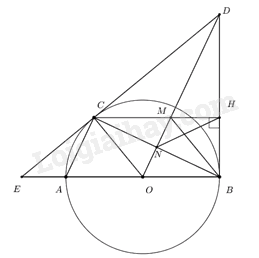
1) Chứng minh: Tứ giác nội tiếp được trong đường tròn.
Do DC, DB là 2 tiếp tuyến của cắt nhau tại D nên (tính chất)
Mà OC = OB (bằng bán kính)
là trung trực của BC (tính chất)
tại N
Xét tứ giác DCNH có () và (cmt)
Mà H, N là 2 đỉnh kề nhau cùng nhìn DC dưới 2 góc bằng nhau
cùng thuộc một đường tròn (dhnb)
Hay tứ giác nội tiếp được trong đường tròn (đpcm)
2) Chứng minh: .
Xét tam giác DBC có DN và CH là đường cao cắt nhau tại M nên M là trực tâm của tam giác DBC
Mà (tiếp tuyến)
Lại có (tiếp tuyến)
là hình bình hành (dhnb)
(tính chất)
Mà (cùng bằng bán kính) nên (đpcm)
3) Các đường thẳng và cắt nhau tại . Chứng minh: .
Xét và có:
chung
(tính chất góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung)
(đpcm)
4) Khi quay tam giác DNB một vòng quanh cạnh DN ta được một hình nón. Biết . Tính thể tích của hình nón tạo thành.
Do vuông tại B, đường cao BN nên ta có
(định lý Pytago)
(hệ thức lượng trong tam giác vuông)
(định lý Pytago)
Khi quay tam giác DNB một vòng quanh cạnh DN ta được một hình nón có chiều cao là DN = 6,4 và đáy là đường tròn có bán kính là BN = 4,8
Suy ra thể tích của hình nón bằng
Vậy thể tích hình nón khoảng