Với a là số thực dương tùy ý, log (100a) bằng

Cho hàm số y = f(x) có đạo hàm f '(x) = x + 1 với mọi x $\in$ R. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Hàm số F(x) = cotx là một nguyên hàm của hàm số nào dưới đây trên khoảng $\left(0;\frac{\pi }{2}\right)$

Cho khối nón có diện tích đáy bằng 3a² và chiều cao 2a. Thể tích của khối nón đã cho bằng ?

Cho hàm số f(x) = ax⁴ + 2(a + 4)x² − 1 với a là tham số thực. Nếu $\underset{[0;2]}{\max }f\left(x\right)$ = f(1) thì $\underset{[0;2]}{\min }f\left(x\right)$ bằng

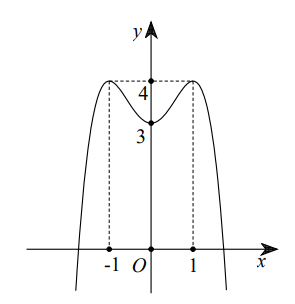
Cho hàm số y = ax⁴ + bx² + c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng

Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng

Cho hàm số f(x) = ax⁴ + bx² + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?

Với a,b là các số thực dương tùy ý và a ≠ 1, ${\log }_{\frac{1}{a}}\frac{1}{b^3}$  bằng

Cho khối lăng trụ đứng ABC.A'BC' có đáy ABC là tam giác vuông cân tại A, cạnh bên AA' = 2a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 30°. Thể tích của khổi lăng trụ đã cho bằng

Cho hàm số f(x) = 1 + e^2x. Khẳng định nào dưới đây là đúng?

Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4^b − 1)(a.3^b − 10) < 0 ?

Cho điểm M nằm ngoài mặt cầu S(O;R). Khẳng định nào dưới đây đúng ?

Cho hàm số bậc ba y = f(x) có đồ thị là đường cong hình bên.

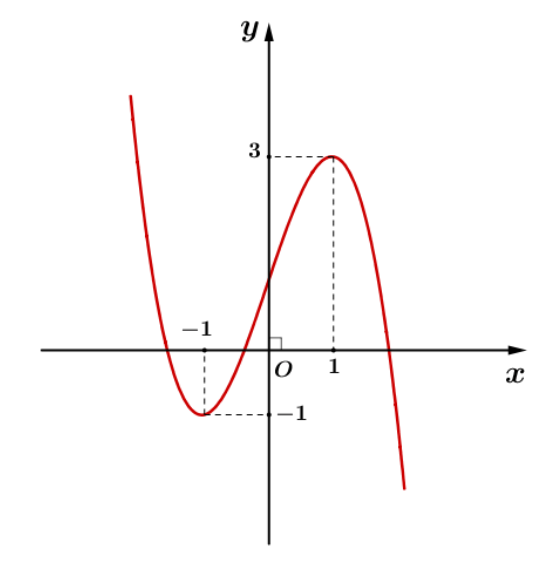
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ

Số nghiệm thực của phương trình $2^{x^2+1}$  = 4 là