Tính các góc của hình thang ABCD (AB, CD là hai đáy) biết ,
 Giải bởi Vietjack
Giải bởi Vietjack
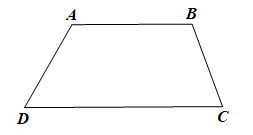
Trong hình thang ABCD có:
và là 2 góc bù nhau, và là 2 góc bù nhau.
Do đó ,
Mà nên , suy ra . Do đó
nên , hay , suy ra
Do đó
Vậy hình thang ABCD có
Phương pháp giải:
• Tính chất về góc: Hai góc kề một cạnh bên của hình thang có tổng bằng 1800 ( nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là hai cạnh đáy)
Hình thang ABCD ( AB // CD) có:
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Hình thang cân (Kết nối tri thức) | Lý thuyết Toán lớp 8
20 câu Trắc nghiệm Hình thang cân (Kết nối tri thức) - Toán lớp 8
Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh đường thẳng SO đi qua trung điểm của AB, đi qua trung điểm của CD.
Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B.
Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với hai đáy).
Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C.
Tính chu vi của hình thang đó biết rằng AD = 2 cm.