Tìm giá trị lớn nhất M của hàm số y = 4sin^2 x + căn 2 sin(2x+pi/4)...

Question

Tìm giá trị lớn nhất M của hàm số y=4sin2x+2sin2x+π4.

VietJack · Accepted Answer

Chọn đáp án D. Ta có y=4sin2x+2sin2x+π4=41−cos2x2+sin2x+cos2x =sin2x−cos2x+2=2sin2x−π4+2. Mà −1≤sin2x−π4≤1⇒−2+2≤2sin2x−π4+2≤2+2 Vậy giá trị lớn nhất của hàm số là 2+2. Phương pháp giải Để tìm được giá trị lớn nhất;giá trị nhỏ nhất của hàm số ta cần chú ý: + Với mọi x ta luôn có: - 1 ≤ cosx ≤ 1; -1 ≤ sinx ≤ 1 +Với mọi x ta có: 0 ≤ |cosx| ≤ 1 ;0 ≤ |sinx| ≤ 1 + Bất đẳng thức bunhia –copski: Cho hai bộ số (a1; a2) và (b1;b2) khi đó ta có: (a1.b1+ a2.b2 )2 ≤ ( a12+ a22 ).( b12+ b22 ) Dấu “=” xảy ra khi: a1/a2 = b1/b2 + Giả sử hàm số y= f(x) có giá trị lớn nhất là M và giá trị nhỏ nhất là m. Khi đó; tập giá trị của hàm số là [m; M]. + Phương trình : a. sinx+ b. cosx= c có nghiệm khi và chỉ khi a2 + b2 ≥ c2 Dạng 1. Sử dụng tính bị chặn của hàm số lượng giác Phương pháp giải: -1 ≤ sin [u(x)] ≤ 1; 0 ≤ sin2[u(x)] ≤ 1; 0 ≤ |sin[u(x)]| ≤ 1 -1 ≤ cos [u(x)] ≤ 1; 0 ≤ cos2[u(x)] ≤ 1; 0 ≤ |cos[u(x)]| ≤ 1 Dạng 2. 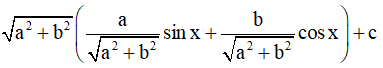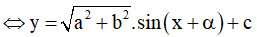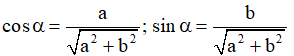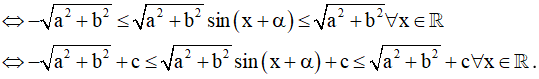Hàm số có dạng y = asinx + bcosx + c (với a, b khác 0) Phương pháp giải: Bước 1: Ta đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]: y = asinx + bcosx + c = với α thỏa mãn Bước 2: Đánh giá -1 ≤ sin (x + α) ≤ 1 ∀x ∈ R Dạng 3: Hàm số có dạng 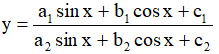Lý thuyết: Phương trình asinx + bcosx = c có nghiệm khi a2 + b2 ≥ c2 (Lý thuyết có trong phần 7) Phương pháp giải: Bước 1: Điều kiện xác định: a2sinx + b2cosx = c2 ≠ 0 Bước 2: 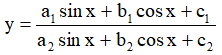⇔ ya2sinx + yb2cosx + yc2 = a1sinx + b1cosx + c1 ⇔ (ya2 - a1)sinx + (yb2 - b1)cosx = -yc + c1 (*) Bước 3: Để phương trình (*) có nghiệm x thì (ya2 - a1)2 + (yb2 - b1)2 ≥ (-yc + c1)2 Tìm đoạn chứa y, sau đó đưa ra kết luận về giá trị lớn nhất và giá trị nhỏ nhất. Tham khảo thêm một số tài liệu liên quan: 30 câu Trắc nghiệm Hàm số lượng giác – Toán lớp 11 15 câu Trắc nghiệm Phương trình lượng giác cơ bản – Toán lớp 11 (Phần 1)

Câu hỏi:

Tìm giá trị lớn nhất M của hàm số $y = 4 \sin^{2} x + \sqrt{2} \sin (2 x + \frac{π}{4}) .$

A. $M = \sqrt{2} .$

B. $M = \sqrt{2} - 1.$

C. $M = \sqrt{2} + 1.$

D. $M = \sqrt{2} + 2.$

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Giải phương trình $\sin (\frac{2 x}{3} - \frac{π}{3}) = 0$

Câu 2:

Số nghiệm của phương trình $\sin (2 x - 40^{0}) = \frac{\sqrt{3}}{2}$ với $- 180^{0} \leq x \leq 180^{0}$ là?

Câu 3:

Trong các hàm số sau, hàm số nào là hàm số chẵn?

Câu 4:

Gọi S là tập nghiệm của phương trình $2 \sin^{2} x + 3 \sqrt{3} \sin x \cos x - \cos^{2} x = 2$ . Khẳng định nào sau đây là đúng?

Câu 5:

Số nghiệm của phương trình $\sin 2 x + \sqrt{3} \cos 2 x = \sqrt{3}$ trên khoảng $(0; \frac{π}{2})$ là?

Câu 6:

Trong các hàm số sau, hàm số nào đồng biến trên khoảng $(- \frac{π}{3}; \frac{π}{6})$ ?

Câu 7:

Hỏi trên $[0; \frac{π}{2})$ , phương trình $2 \sin^{2} x - 3 \sin x + 1 = 0$ có bao nhiêu nghiệm?

Câu 8:

Tìm chu kì T của hàm số $y = 2 \sin^{2} x + 3 \cos^{2} 3 x .$

Câu 9:

Cho hàm số $y = - 2 \sin (x + \frac{π}{3}) + 2$ . Mệnh đề nào sau đây là đúng?

Câu 10:

Số nghiệm của phương trình $\frac{1}{\sin^{2} x} - (\sqrt{3} - 1) \cot x - (\sqrt{3} + 1) = 0$ trên $(0; π)$ là

Câu 11:

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?

Câu 12:

Tìm chu kì T của hàm số $y = \cos 2 x + \sin \frac{x}{2} .$

Câu 13:

Tìm chu kì T của hàm số $y = - \frac{1}{2} \sin (100 π x + 50 π) .$

Câu 14:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình $\cos (2 x - \frac{π}{3}) - m = 2$ có nghiệm. Tính tổng T của các phần tử trong S.

Đề thi liên quan

Câu hỏi mới nhất

Câu hỏi:

Tìm giá trị lớn nhất M của hàm số y=4sin2x+2sin2x+π4.

A. M=2.

B. M=2−1.

C. M=2+1.

D. M=2+2.