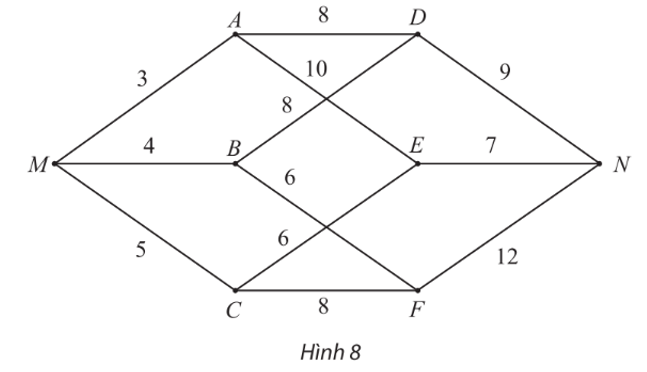
Tìm đường đi ngắn nhất từ đỉnh M đến N trong đồ thị có trọng số sau:
 Giải bởi Vietjack
Giải bởi Vietjack
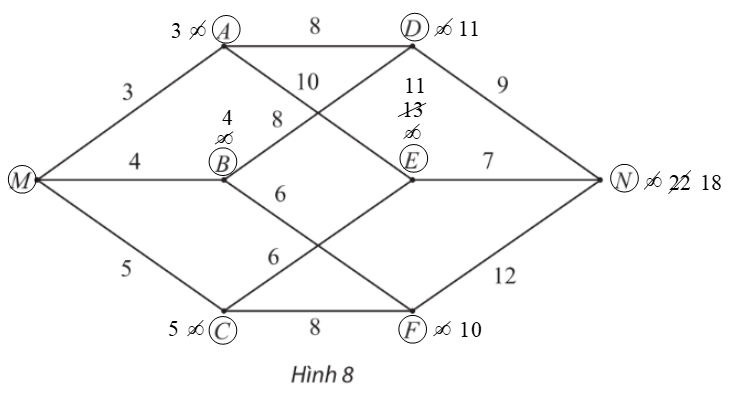
– Gán nhãn cho M bằng 0 (tức là, nM = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh M.
– Tại các đỉnh kề với M, gồm A, B, C, ta có:
⦁ nA = nM + wMA = 0 + 3 = 3. Vì 3 < ∞ nên ta đổi nhãn của A thành 3.
⦁ nB = nM + wMB = 0 + 4 = 4. Vì 4 < ∞ nên ta đổi nhãn của B thành 4.
⦁ nC = nM + wMC = 0 + 5 = 5. Vì 5 < ∞ nên ta đổi nhãn của C thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là A nên ta khoanh tròn đỉnh A (đỉnh gần M nhất, chỉ tính các điểm khác M).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với A gồm D, E, ta có:
⦁ nD = nA + wAD = 3 + 8 = 11. Vì 11 < ∞ nên ta đổi nhãn của D thành 11.
⦁ nE = nA + wAE = 3 + 10 = 13.Vì 13 < ∞ nên ta đổi nhãn của E thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần M thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với B gồm D, F, ta có:
⦁ nD = nB + wBD = 4 + 8 = 12. Vì 12 > 11 (11 là nhãn hiện tại của D) nên ta giữ nguyên nhãn của D là 11.
⦁ nF = nB + wBF = 4 + 6 = 10. Vì 10 < ∞ nên ta đổi nhãn của F thành 10.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C nên ta khoanh tròn đỉnh C (đỉnh gần M thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với C gồm E, F, ta có:
⦁ nE = nC + wCE = 5 + 6 = 11. Vì 11 < 13 (13 là nhãn hiện tại của E) nên ta đổi nhãn của E thành 11.
⦁ nF = nC + wCF = 5 + 8 = 13. Vì 13 > 10 (10 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 10.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần M thứ tư).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với F chỉ có N, ta có:
nN = nF + wFN = 10 + 12 = 22. Vì 22 < ∞ nên ta đổi nhãn của N thành 22.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D, E nên ta tùy ý khoanh tròn đỉnh E (đỉnh gần M thứ năm).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với E chỉ có N, ta có:
nN = nE + wEN = 11 + 7 = 18. Vì 18 < 22 (22 là nhãn hiện tại của N) nên ta đổi nhãn của N thành 18.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta tùy ý khoanh tròn đỉnh D (đỉnh gần M thứ sáu).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với D chỉ còn N, ta có:
nN = nD + wDN = 11 + 9 = 20. Vì 20 > 18 (18 là nhãn hiện tại của N) nên ta giữ nguyên nhãn của N là 18.
Lúc này, ta thấy chỉ còn đỉnh N chưa được khoanh tròn nên ta khoanh tròn đỉnh N (đỉnh gần M thứ bảy).
– Nhìn lại các bước trên, ta thấy:
nN = 18 = nE + wEN = nC + wCE + wEN = nM + wMC + wCE + wEN
= wMC + wCE + wEN = lMCEN.
Vậy MCEN là đường đi ngắn nhất từ đỉnh M đến N, với độ dài bằng 18.
Cho đồ thị ở Hình 3, phát biểu nào sau đây đúng?
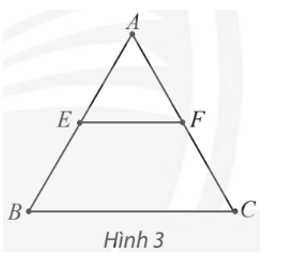
A. Đồ thị có chu trình Euler.
B. Đồ thị đường đi Euler xuất phát từ đỉnh A.
C. Đồ thị đường đi Euler xuất phát từ đỉnh E.
D. Đồ thị không có đường đi Euler.
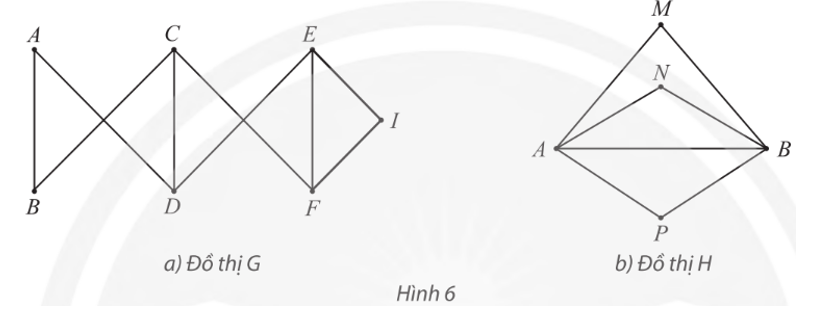
Mỗi đồ thị trong Hình 6 có chu trình Hamilton không? Nếu có hãy chỉ ra một chu trình như vậy. Nếu không, đồ thị có đường đi Hamilton không? Nếu có, hãy chỉ ra một đường đi như vậy.
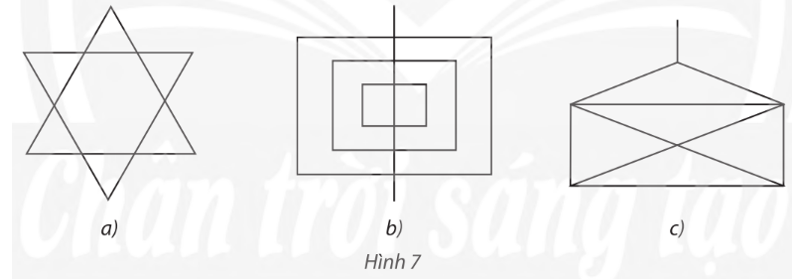
Có thể vẽ mỗi hình sau đây bằng một nét liền, không nhấc bút khỏi giấy, không vẽ lại đoạn đường nào hai lần không? Nếu có, hãy chỉ ra một cách vẽ.
Cho tập hợp số V = {1; 2; 3; 4; 5; 6; 7}. Hãy vẽ đồ thị G có các đỉnh biểu diễn các phần tử của V, hai đỉnh biểu diễn hai số m và n kề nhau nếu m + n là bội của 3.
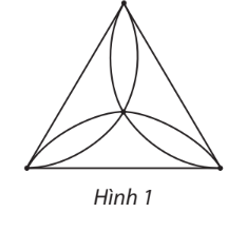
Tổng tất cả bậc của các đỉnh của đồ thị ở Hình 1 là
A. 20.
B. 18.
C. 12.
D. 9.
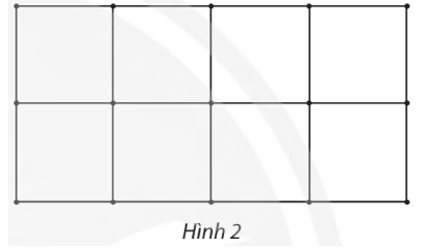
Đồ thị ở Hình 2 có bao nhiêu đỉnh bậc lẻ?
A. 6.
B. 7.
C. 8.
D. 9.
Số đỉnh, số cạnh của đồ thị ở Hình 1 lần lượt là
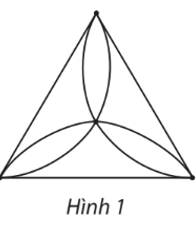
A. 3 đỉnh, 8 cạnh.
B. 4 đỉnh, 8 cạnh.
C. 3 đỉnh, 9 cạnh.
D. 4 đỉnh, 9 cạnh.
Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là
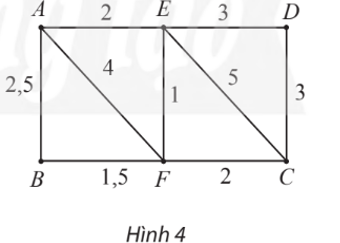
A. AEC.
B. AEFC.
C. AC.
D. AFC.
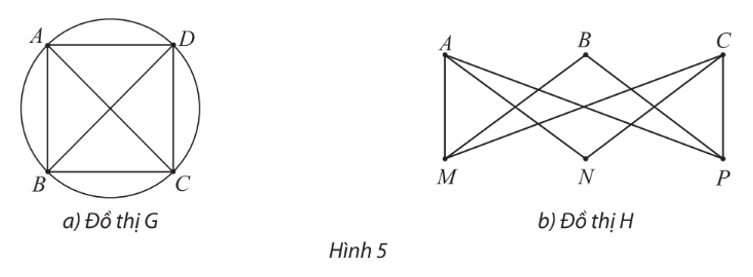
Mỗi đồ thị trong Hình 5 có chu trình Euler không? Nếu có hãy chỉ ra một chu trình như vậy. Nếu không, đồ thị có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.