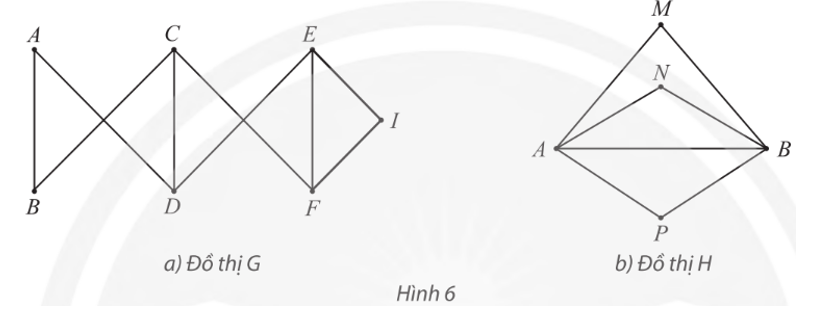
Mỗi đồ thị trong Hình 6 có chu trình Hamilton không? Nếu có hãy chỉ ra một chu trình như vậy. Nếu không, đồ thị có đường đi Hamilton không? Nếu có, hãy chỉ ra một đường đi như vậy.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Đồ thị G:
Đồ thị G có các đỉnh A, B, I có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh AB, AD, BC, EI, FI.
Do đó ta có một chu trình Hamilton h của đồ thị G là: CBADEIFC.
b) Đồ thị H:
Đồ thị H có các đỉnh M, N, P có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh MA, MB, NA, NB, PA, PB.
Ta thấy chu trình Hamilton h (nếu có) đi qua ba cạnh MA, NA, PA nối với đỉnh A nên chu trình Hamilton h không tồn tại.
Đồ thị H có đường đi Hamilton, chẳng hạn MANBP.
Vậy đồ thị G không có chu trình Hamilton và cũng không có đường đi Hamilton; đồ thị H không có chu trình Hamilton và có đường đi Hamilton.
Cho đồ thị ở Hình 3, phát biểu nào sau đây đúng?
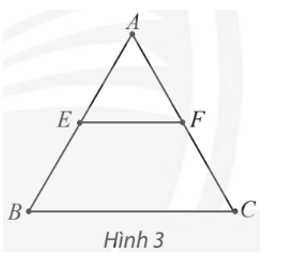
A. Đồ thị có chu trình Euler.
B. Đồ thị đường đi Euler xuất phát từ đỉnh A.
C. Đồ thị đường đi Euler xuất phát từ đỉnh E.
D. Đồ thị không có đường đi Euler.
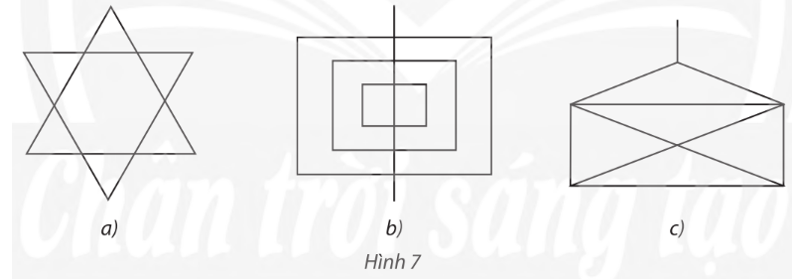
Có thể vẽ mỗi hình sau đây bằng một nét liền, không nhấc bút khỏi giấy, không vẽ lại đoạn đường nào hai lần không? Nếu có, hãy chỉ ra một cách vẽ.
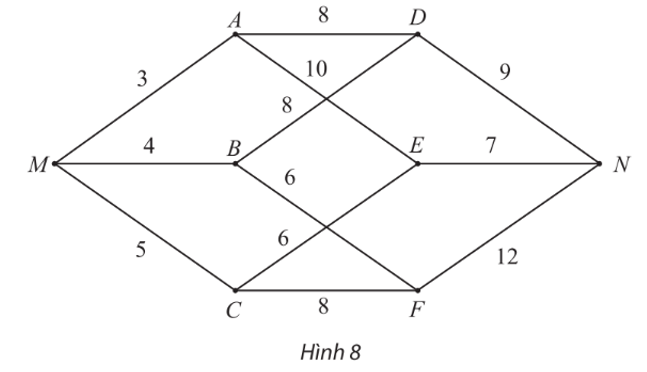
Tìm đường đi ngắn nhất từ đỉnh M đến N trong đồ thị có trọng số sau:
Cho tập hợp số V = {1; 2; 3; 4; 5; 6; 7}. Hãy vẽ đồ thị G có các đỉnh biểu diễn các phần tử của V, hai đỉnh biểu diễn hai số m và n kề nhau nếu m + n là bội của 3.
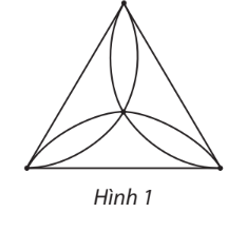
Tổng tất cả bậc của các đỉnh của đồ thị ở Hình 1 là
A. 20.
B. 18.
C. 12.
D. 9.
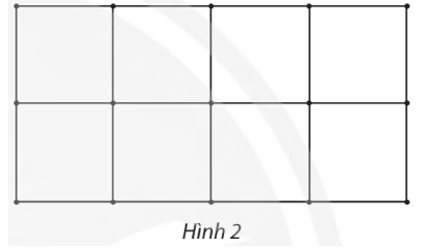
Đồ thị ở Hình 2 có bao nhiêu đỉnh bậc lẻ?
A. 6.
B. 7.
C. 8.
D. 9.
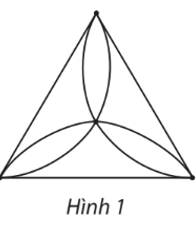
Số đỉnh, số cạnh của đồ thị ở Hình 1 lần lượt là
A. 3 đỉnh, 8 cạnh.
B. 4 đỉnh, 8 cạnh.
C. 3 đỉnh, 9 cạnh.
D. 4 đỉnh, 9 cạnh.
Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là
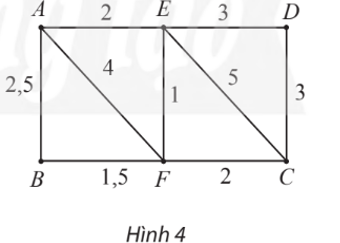
A. AEC.
B. AEFC.
C. AC.
D. AFC.
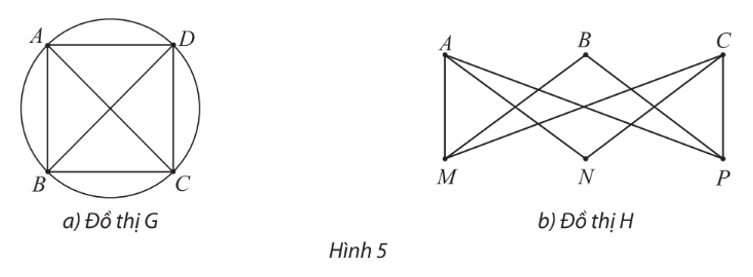
Mỗi đồ thị trong Hình 5 có chu trình Euler không? Nếu có hãy chỉ ra một chu trình như vậy. Nếu không, đồ thị có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.