Tam giác ABC có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
A. 2S
B. 3S
C. 4S
D. 6S
Giải bởi Vietjack
Lời giải
Đáp án đúng là D
Diện tích tam giác ABC ban đầu là: S = \(\frac{1}{2}\). BC.AC.sinC
Diện tích tam giác ABC lúc sau là: Ss = \(\frac{1}{2}\).2BC.3AC.sinC = 6. \(\frac{1}{2}\). BC.AC.sinC = 6S.
Vậy đáp án đúng là D.
Công thức, cách tính Diện tích tam giác:
Cho tam giác ABC có BC = a, CA = b và AB = c, gọi ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB; R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác;
Bài tập liên quan:
Một tháp viễn thông cao 42 m được dựng thẳng đứng trên một sườn dốc 34° so với phương ngang. Từ đỉnh tháp người ta neo một sợi cáp xuống một điểm trên sườn dốc cách chân tháp 33 m như Hình 2. Tính chiều dài của sợi dây cáp đó.
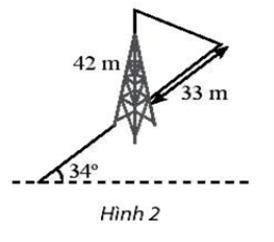
Cách giải:
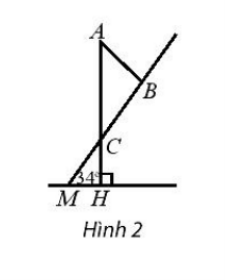
Ta biểu diễn lại hình như trên. AB là độ dài sợi dây cáp. AC là độ dài tháp. Như vậy AC = 42 m, BC = 33 m, \(\widehat {{\rm{CMH}}}\) = 34°, \(\widehat {{\rm{MHC}}}\)= 90°.
Xét tam giác MCH: \(\widehat {{\rm{MCH}}} + \widehat {{\rm{MHC}}} + \widehat {{\rm{CMH}}}\) = 180°.
⇒ \(\widehat {{\rm{MCH}}}\) = 180° – 90° – 34° = 56°.
\(\widehat {{\rm{ACB}}}\) và \(\widehat {{\rm{MCH}}}\)là hai góc đối đỉnh nên \(\widehat {{\rm{ACB}}}\) = 56° ( tính chất hai góc đối đỉnh).
Áp dụng định lí côsin cho tam giác ABC:
AB2 = AC2 + BC2 – 2.AC.BC.cos\(\widehat {{\rm{ACB}}}\)
AB2 = 422 + 332 – 2.42.33.cos56°
AB = \[\sqrt {{{42}^2} + {\rm{ }}{{33}^2}--{\rm{ }}2.42.33.{\rm{cos}}56^\circ } \]
AB ≈ 36,1 m
Vậy chiều dài sợi dây cáp khoảng 36,1 m.
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Chương 4: Vecto (Kết nối tri thức) | Toán lớp 10
30 câu Trắc nghiệm Chương 4: Vectơ (Kết nối tri thức) – Toán lớp 10
Khẳng định nào sau đây là đúng?
A. sinα = sin( 180° – α );
B. cosα = cos( 180° – α );
C. tanα = tan( 180° – α );
D. cotα = cot( 180° – α );
Trong các khẳng định sau đây, khẳng định nào sai?
A. cos45° = sin45°;
B. cos45° = sin135°;
C. cos30° = sin120°;
D. sin60° = cos120°.
Cho tam giác ABC có BC = a, AC = b, AB = c. Mệnh đề nào sau đây đúng?
A. Nếu b2 + c2 – a2 > 0 thì góc A nhọn;
B. Nếu b2 + c2 – a2 > 0 thì góc A tù;
C. Nếu b2 + c2 – a2 < 0 thì góc A nhọn;
D. Nếu b2 + c2 – a2 < 0 thì góc A vuông.
Cho tam giác ABC vuông cân tại A có AB = AC = 30 cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC là:
A. 50 cm2;
B. 50\(\sqrt 2 \) cm2;\(\)
C. 75 cm2;
D. 15\(\sqrt {105} \) cm2.
Cho \(\widehat {{\rm{xOy}}}\) = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
A. 1,5;
B. \(\sqrt 3 \);
C. \(2\sqrt 2 \);
D. 2.
Trong các đẳng thức sau đây, đẳng thức nào là đúng?
A. sin150° = \(\frac{{ - \sqrt 3 }}{2}\);
B. cos150° = \(\frac{{\sqrt 3 }}{2}\);
C. tan150° = \(\frac{{ - 1}}{{\sqrt 3 }}\);
D. cot150° = \(\sqrt 3 \).
Cho tam giác ABC có AB = 4 cm, BC = 7 cm, CA = 9 cm. Giá trị cosA là:
A. \(\frac{2}{3}\);
B. \(\frac{1}{3}\);
C. \(\frac{{ - 2}}{3}\);
D. \(\frac{1}{2}\).
Cho tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64cm2. Giá trị sinA là:
A. \(\frac{{\sqrt 3 }}{2}\);
B. \(\frac{3}{8}\);
C. \(\frac{4}{5}\);
D. \(\frac{8}{9}\).
Cho tam giác ABC không vuông. Chứng minh rằng:
\[\frac{{\tan {\rm{A}}}}{{\tan {\rm{B}}}} = \frac{{{{\rm{c}}^2} + {{\rm{a}}^2} - {{\rm{b}}^2}}}{{{{\rm{c}}^2} + {{\rm{b}}^2} - {{\rm{a}}^2}}}\].
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
