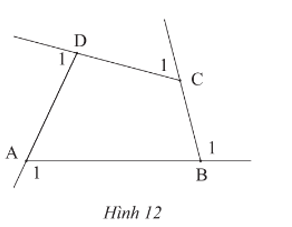
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó. Hãy tính tổng số đo bốn góc ngoài góc A1, góc B1, góc C1, góc D1 của tứ giác...

Question

Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó. Hãy tính tổng số đo bốn góc ngoài A^1,B^1,C^1,D^1 của tứ giác ABCD ở Hình 12.

VietJack · Accepted Answer

Xét tứ giác ABCD có: A^2+B^2+C^2+D^2=360° (định lí tổng các góc của một tứ giác) Mặt khác: A^1+A^2=180° (hai góc kề bù) Tương tự: B^1+B^2=180°; C^1+C^2=180°; D^1+D^2=180° Suy ra A^1+A^2+B^1+B^2+C^1+C^2+D^1+D^2=180°+180°+180°+180° Hay A^1+B^1+C^1+D^1+A^2+B^2+C^2+D^2=720° Do đó A^1+B^1+C^1+D^1+360°=720° Nên A^1+B^1+C^1+D^1=720°−360°=360°. Vậy tổng số đo bốn góc ngoài A^1,B^1,C^1,D^1 của tứ giác ABCD bằng 360°. Phương pháp giải: Định lí tổng các góc của một tứ giác Tổng số đo các góc của một tứ giác bằng 3600. Tứ giác ABCD, A^+B^+C^+D^=3600 Hai góc kề bù • Định nghĩa: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù. • Tính chất: Hai góc kề bù có tổng số đo bằng 180°. => Muốn tìm góc chưa biết ta lấy 1800 - góc đã biết Chú ý: • Hai góc kề bù được hiểu là hai góc vừa kề nhau, vừa bù nhau. Trong đó: - Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía nhau đối với đường thẳng chứa cạnh chung đó. Tham khảo thêm một số tài liệu liên quan: Lý thuyết Tứ giác (Chân trời sáng tạo) | Lý thuyết Toán lớp 8 20 câu Trắc nghiệm Tứ giác (Chân trời sáng tạo) - Toán lớp 8

Câu hỏi:

Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.

Hãy tính tổng số đo bốn góc ngoài ${\hat{A}}_{1}, {\hat{B}}_{1}, {\hat{C}}_{1}, {\hat{D}}_{1}$ của tứ giác ABCD ở Hình 12.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

Câu 2:

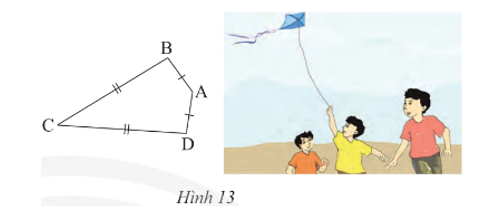
Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của BD.

Câu 3:

Tứ giác ABCD có $\hat{A} = 100 °$ , góc ngoài tại đỉnh B bằng 110°, $\hat{C} = 75 °$ . Tính số đo góc D.

Câu 4:

Tứ giác ABCD có góc ngoài tại đỉnh A bằng 65°, góc ngoài tại đỉnh B bằng 100°, góc ngoài tại đỉnh C bằng 60°. Tính số đo góc ngoài tại đỉnh D.

Câu 5:

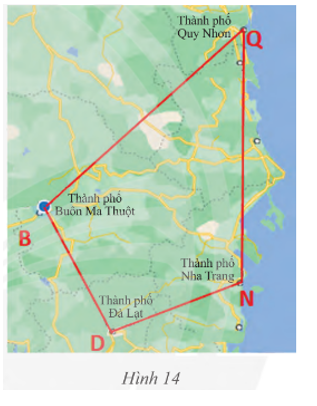
Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.

a) Tìm các cạnh kề và cạnh đối của cạnh BD.

Câu 6:

b) Cho biết $\hat{B} = 95 °$ , $\hat{C} = 35 °$ . Tính $\hat{A}$ và $\hat{D}$ .

Câu 7:

Tứ giác ABCD có số đo $\hat{A} = x, \hat{B} = 2 x, \hat{C} = 3 x, \hat{D} = 4 x$ . Tính số đo các góc của tứ giác đó.

Câu 8:

Tìm x trong mỗi tứ giác sau:

Câu 9:

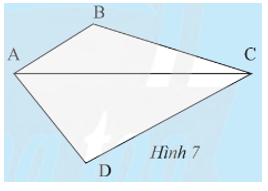
Đường chéo AC chia tứ giác ABCD thành hai tam giác ACB và ACD (Hình 7). Tính tổng các góc của tam giác ACB và tam giác ACD. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác ABCD?

Câu 10:

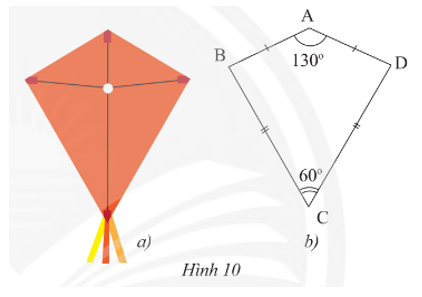
Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

Câu 11:

Vẽ tứ giác MNPQ và tìm:

‒ Hai đỉnh đối nhau;

‒ Hai đường chéo;

‒ Hai cạnh đối nhau.

Câu 12:

b) Tìm các đường chéo của tứ giác.

Câu 13:

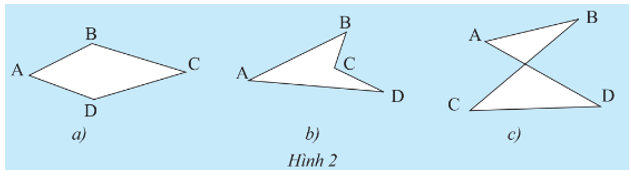
Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của các cạnh còn lại của tứ giác đối với mỗi đường thẳng đã vẽ.

Câu 14:

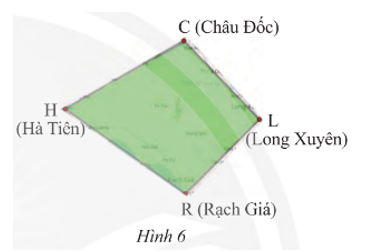
Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL (Hình 6).

Đề thi liên quan

Câu hỏi mới nhất