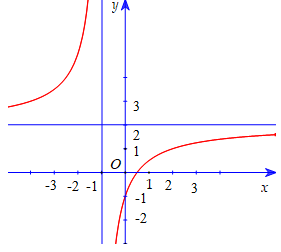
Đồ thị sau đây là của hàm số nào?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A.
Tiệm cận đứng của hàm số là x = -1 và tiệm cận ngang của hàm số là y = 2 nên loại B và C.
Ta nhận thấy đồ thị đi qua điểm (0; -1) nên thỏa mãn đồ thị hàm số ý A.
Sơ đồ chung về khảo sát và vẽ đồ thị: Gồm 3 bước:
Bước 1: Tập xác định
- Tìm tập xác định
- Xét tính chẵn, lẻ nếu có.
Bước 2: Chiều biến thiên
- Tính các giới hạn.
- Tìm các tiệm cận đứng và tiệm cận ngang.
- Tính đạo hàm cấp một, dấu luôn dương hay âm
- Lập bảng biến thiên rồi chỉ ra các khoảng đồng biến, hay các khoảng nghịch biến.
Bước 3: Vẽ đồ thị
- Cho vài giá trị đặc biệt, giao điểm với hai trục tọa độ.
- Vẽ đúng đồ thị, lưu ý tâm đối xứng là giao điểm 2 tiệm cận đứng và tiệm cận ngang.
Các dạng đồ thị hàm hữu tỉ 1/1: với
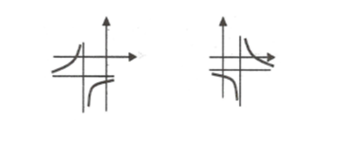
Bài tập liên quan:
Đồ thị dưới đây là của hàm số nào?
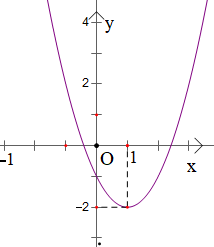
A. y = -x2 - 2x +3
B. y = x2 +2x -2
C. y = 2x2 - 4x -2
D. y= x2 - 2x - 1
Lời giải:
Đáp án đúng là: D
- Do parabol có bề lõm quay lên trên nên a > 0, ta loại A.
- Trục đối xứng của parabol là đường thẳng
Do đó ta loại B vì y = x2 + 2x – 2 có a = 1, b = 2 nên có trục đối xứng
- Quan sát đồ thị ta thấy x = 0 thì y = ‒1
Do đó ta loại C vì với x = 0 thì y = 2x2 – 4x – 2 = 2.02 – 4.0 – 2 = – 2 ≠ – 1.
Vậy đồ thị trên là của hàm số y = x2 – 2x – 1.
Tham khảo thêm một số tài liệu liên quan:
Chuyên đề Ứng dụng đạo hàm để Khảo sát hàm số
Bài tập Vận dụng cao - Đồ thị của hàm hợp có lời giải chi tiết
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
Cho hàm số với a > 0 có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
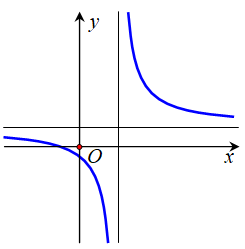
Cho hàm số với a > 0 có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

Cho biết hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên. Trong các khẳng định sau, khẳng định nào đúng?
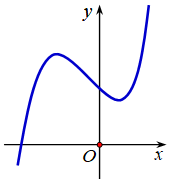
Cho biết hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên. Trong các khẳng định sau, khẳng định nào đúng?

Hàm số đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
Hàm số đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
Tìm m để hàm số y = x4 – 2mx2 + 2m + m4 – 5 đạt cực tiểu tại x = -1
Tìm m để hàm số y = x4 – 2mx2 + 2m + m4 – 5 đạt cực tiểu tại x = -1