A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Phương trình trục hoành là:
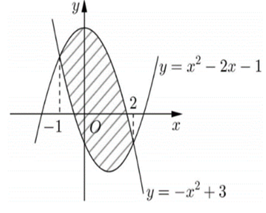
x2 – 2x −1 = −x2 + 3
Û −x2 + 3 – x2 + 2x + 1 = 0
Û −2x2 + 2x + 4 = 0
Û
Diện tích hình phẳng giới hạn bởi y = x2 – 2x – 1 và y = −x2 + 3 là:
S =