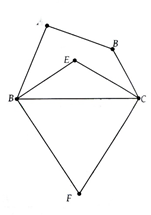
Cho tứ giác ABCD biết = 4:3:2:1.
a) Tính các góc của tứ giác ABCD.
b) Các tia phân giác của cắt nhau tại E. Các đường phân giác của góc ngoài tại các đỉnh C và D cắt nhau tại F. Tính
Giải bởi Vietjack
a) Sử dụng tính chất dãy tỉ số bằng nhau.
b) Sử dụng tổng ba góc trong tam giác tính được .
Chú ý hai phân giác trong và ngoài tại mỗi góc của một tam giác thì vuông góc nhau, cùng với tổng bốn góc trong tứ giác, ta tính được
Phương pháp giải:
Tính chất dãy tỉ số bằng nhau:
Dãy tỉ số có dạng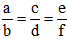 
... được gọi là dãy tỉ số bằng nhau.
Các công thức
Với điều kiện các tỉ số đều có nghĩa, ta có:
Tham khảo thêm một số tài liệu liên quan:
Cho tứ giác ABCD, AB Cắt CD tại E, BC cắt AD tại F. Các tia phân giác của cắt nhau tại I. Chứng minh
a)
b) Nếu thì
Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo;
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy.
Cho tứ giác ABCD có và BC = AD. Chứng minh:
a) ∆DAB = ∆CBA, từ đó suy ra BD = AC;
b)
c) AB // CD
Cho tứ giác ABCD và một điểm M thuộc miền trong của tứ giác. Chứng minh:
a) MA + MB + MC + MD≥ AB + CD;
b) MA + MB + MC + MD ≥ 0.5(AB + BC + CD + DA)
a) Chứng minh trong một tứ giác có hai đường chéo vuông góc, tổng bình phương của hai cạnh đối này bằng tổng các bình phương của hai cạnh đối kia.
b) Tứ giác ABCD có AC vuông góc với BD. Biết AD = 5cm, AB = 2 cm, BC = 10 cm. Tính độ dài CD
Cho tứ giác ABCD có AB = AD, CB = CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).
a) Chứng minh AC là đường trung trực của BD.
b) Tính
Tứ giác ABCD có Các tia phân giác của cắt nhau tại I và = 1150. Tính các góc
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
