Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính $\left(\overrightarrow{CB},\overrightarrow{CA}\right)$.

Hướng dẫn giải:

Đáp án đúng là: C.

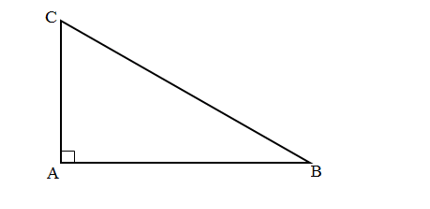
Xét tam giác ABC vuông tại A có:

$\sin \widehat{ACB}=\frac{AB}{BC}=\frac{4}{8}=\frac{1}{2}\Rightarrow \widehat{ACB}=30°$

Vậy $\left(\overrightarrow{CB},\overrightarrow{CA}\right)=\widehat{ACB}=30°$.

Phương pháp giải

Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ

Định nghĩa góc giữa hai vectơ: Cho hai vectơ  đều khác vectơ-không. Từ một điểm O bất kỳ, ta vẽ các vectơ . Khi đó số đo của góc AOB, được gọi là số đo góc giữa hai vectơ , hoặc đơn giản là góc giữa hai vectơ .

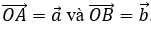
Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ.

Sử dụng công thức sau:

Cho hai vectơ 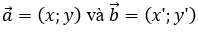. Khi đó

Chú ý: Góc giữa hai vectơ thuộc [0°;180°]

Bài tập liên quan: 

Cho hình thoi ABCD tâm O. Biết BD = $2\sqrt{3}$, AC = 6. Tính $\left(\overrightarrow{BA},\overrightarrow{BC}\right)$.

A. 180°;

B. 120°;

C. 30°;

D. 65°.

Cách giải:

Đáp án đúng là: B.

Hình thoi ABCD có tâm O nên O là trung điểm của hai đường chéo AC và BD, hơn nữa hai đường chéo này vuông góc với nhau tại O.

Do đó, ta có:

BD = $2\sqrt{3}\Rightarrow OB=\sqrt{3}$

AC = 6 ⇒ AO = 3.

Xét tam giác AOB vuông tại O có: $\tan \widehat{ABO}=\frac{AO}{OB}=\frac{3}{\sqrt{3}}\Rightarrow \widehat{ABO}=60°$.

Do ABCD là hình thoi nên BD là tia phân giác góc $\widehat{ABC}$, do đó ta có:

$\widehat{ABC}=2\widehat{ABO}=2.60°=120°$.

Vậy $\left(\overrightarrow{BA},\overrightarrow{BC}\right)=\widehat{ABC}=120°$.

Tham khảo thêm một số tài liệu liên quan:

Bài tập tự luyện Góc giữa hai vectơ chọn lọc

Bài tập tự luyện Tích vô hướng của hai vectơ chọn lọc