Cho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC.
a) Hãy so sánh hai góc MAB và MAC.
(HD. Lấy điểm P sao cho M là trung điểm của AP rồi chứng minh hai tam giác AMC và PMB bằng nhau).
Giải bởi Vietjack
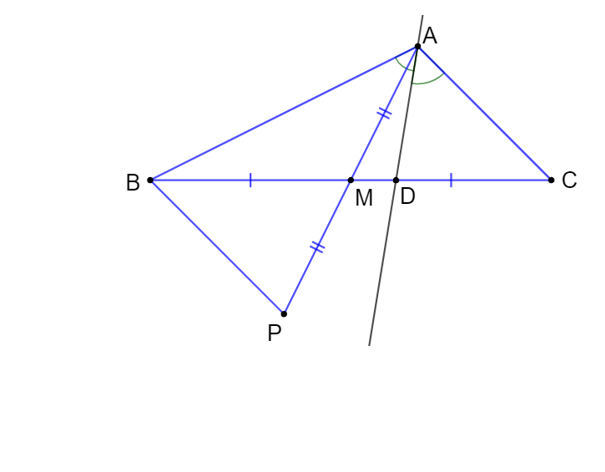
a) Lấy P là điểm thuộc đường thẳng AM sao cho M là trung điểm của AP.
Xét hai tam giác ∆ AMC và ∆ PMB có:
AM = PM (M là trung điểm của AP)
MC = MB (M là trung điểm của BC)
(hai góc đối đỉnh)
Do đó ∆AMC = ∆PMB (c.g.c)
Suy ra (hai góc tương ứng) (1)
Và AC = PB
Mà AB > AC (gt)
Nên suy ra AB > PB
Xét tam giác ABP có AB > PB (cmt) nên theo định lí 1 ta có (2)
Từ (1) và (2) suy ra (3).
Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 60°.
Cho tam giác ABC cân tại A, hai điểm D, E nằm trên đường thẳng BC, D nằm giữa B và C, C nằm giữa D và E. Chứng minh AD < AC < AE.
Hãy giải thích tại sao trong tam giác vuông, cạnh huyền dài nhất và trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.
b) Tia phân giác của góc BAC cắt BC tại D. Hỏi D thuộc đoạn thẳng MB hay đoạn thẳng MC? Vì sao?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
