Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = 2a. Góc giữa đường thẳng BC' và mặt phẳng (ACC'A') bằng 30°. Thể tích của khối lăng trụ đã cho bằng
A. 3a3;
B. a3;
C.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
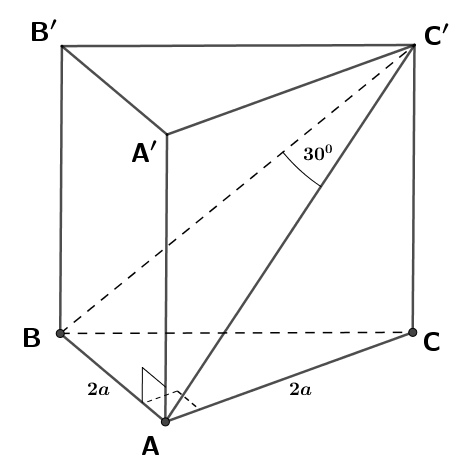
Ta có:
Vậy góc giữa đường thẳng BC' và mặt phẳng (ACC'A') là .
Trong tam giác vuông (BC'A) ta có
Trong tam giác vuông ACC' ta có .
Vậy thể tích khối lăng trụ đã cho là:
Phương pháp giải:
+) Công thức thể tích khối lăng trụ:
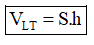
với: S: Diện tích đáy
h: Chiều cao.
+) Phương pháp tính thể tích lăng trụ
Bước 1: Xác định và tính chiều cao của khối lăng trụ
+) Trong nhiều trường hợp, chiều cao của khối đa diện được cho ngay từ đầu bài (chiều cao cho trực tiếp), nhưng cũng có trường hợp việc xác định phải dựa vào các định lí về quan hệ vuông góc (chiều cao cho gián tiếp), hay dùng nhất là: định lí 3 đường vuông góc, các định lí về điều kiện để một đường thẳng vuông góc với một mặt phẳng, …
+) Tính độ dài chiều cao: Sử dụng định lí Pitago, hoặc nhờ hệ thức lượng trong tam giác vuông, tỉ số lượng giác trong tam giác vuông, định lý cosin, …
+) Có thể tính chiều cao bằng cách chuyển về bài toán tìm khoảng cách từ một điểm đến một mặt phẳng.
Nếu OA // (α) thì d(O,(α)) = d(A,(α))
Nếu 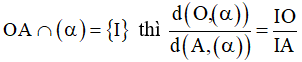 (định lý Ta-lét)
(định lý Ta-lét)
Bước 2: Tìm diện tích đáy bằng các công thức.
Bước 3: Sử dụng công thức tính thể tích.
Tham khảo thêm một số kiến thức liên quan
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |x4 - 2mx2 + 64x| có đúng ba điểm cực trị
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng ba số nguyên b thỏa mãn (3b - 3)(a.2b - 18) < 0?
Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 8(z1 + z2)z3 = 3z1z2. Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho hàm số f (x) = (m - 1)x4 - 2mx2 + 1 với m là tham số thực. Nếu thì bằng
Cho khối lăng trụ có diện tích đáy là 3a2 và chiều cao 2a. Thể tích khối lăng trụ đã cho bằng
Trong không gian Oxyz, cho điểm A(1; 2; -2). Gọi (P) là mặt phẳng chứa trục Ox sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là
Cho hình nón có góc ở đỉnh là 120° và chiều cao bằng 4. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Tính diện tích của (S) bằng:
Cho khối chóp S.ABC có chiều cao bằng 3, đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng
Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
Trong không gian Oxyz, cho mặt cầu (S) tâm I(1; 3; 9) bán kính bằng 3. Gọi M , N là hai điểm lần lượt thuộc hai trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (S), giá trị AM.AN bằng
Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + x - 3y bằng