Cho hàm số f (x) = (m - 1)x4 - 2mx2 + 1 với m là tham số thực....

Question

Cho hàm số f (x) = (m - 1)x4 - 2mx2 + 1 với m là tham số thực. Nếu min0; 3fx=f2 thì max0; 3fx bằng

VietJack · Accepted Answer

Đáp án đúng là: B Phương pháp giải: - Tính đạo hàm f′(x)f′(x) của hàm số, tìm nghiệm của phương trình f′(x)=0f′(x)=0. - Dựa vào điều kiện min[0;3]f(x)=f(2)min[0;3]⁡f(x)=f(2) để đánh giá, tìm ra mm. - Thay mm vào hàm số và tìm max[0;3]f(x)max[0;3]⁡f(x). Giải chi tiết: Ta có: f '(x) = 4(m - 1)x3 - 4mx = 4x[(m - 1)x2 - m] f '(x) = 0 ( m = 1 không thỏa yêu cầu bài toán) Vì min0; 3fx=f2 Þ x = 2 là nghiệm của f '(x) = 0 ⇒mm−1=4⇒m=4m−4⇒m=43 ⇒fx=13x4−83x2+1 f (0) = 1;f3=813−723+33=123=4 Vậy max0; 3fx=4. Bài tập liên quan: Cho hàm số f (x) = mx4 + 2(m - 1)x2 với m là tham số thực. Nếu min0; 2fx=f1 thì max0; 2fx bằng? 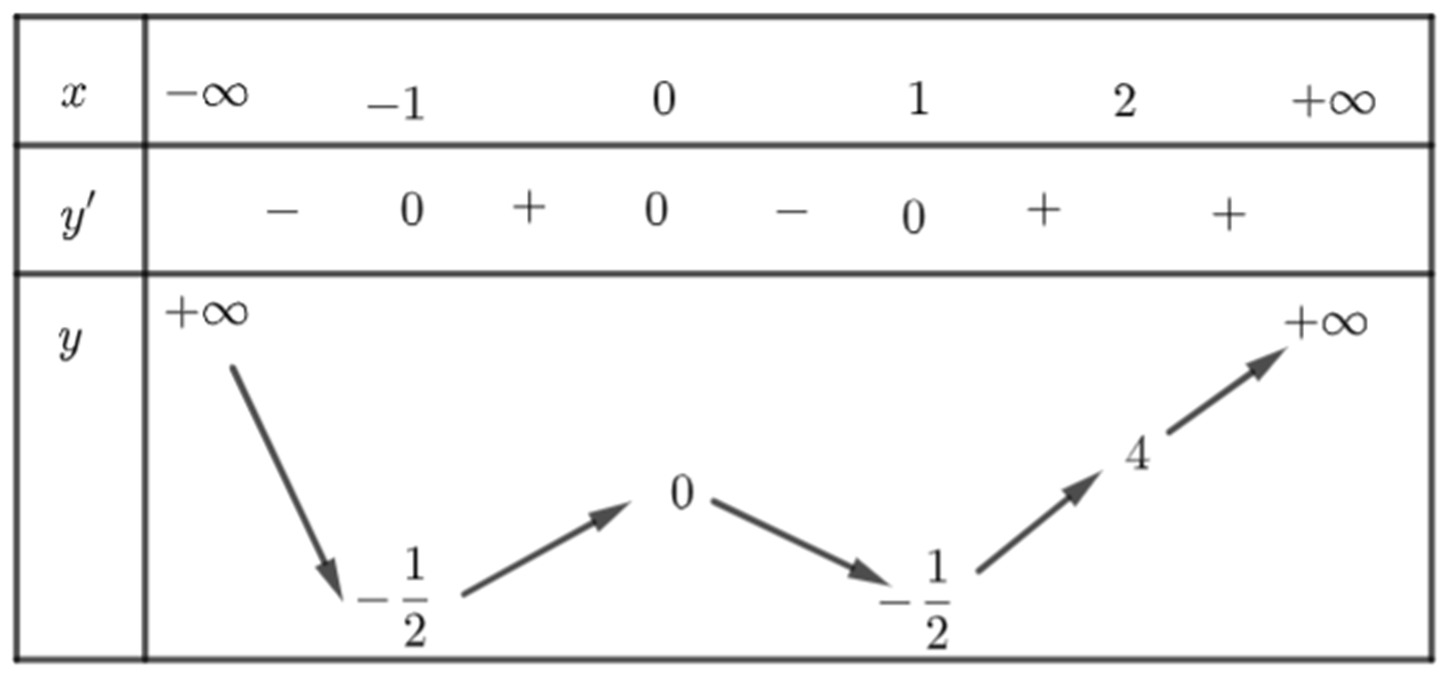Lời giải: f '(x) = 4mx3 + 4(m - 1)x Do f (x) là hàm đa thức và min0; 2fx=f1⇒f'1=0 ⇔4m+4m−1=0⇒m=12 Thay =12 vào hàm số ban đầu ta được y=12x4+212−1x2=12x4−x2 Þ y' = 2x3 - 2x = 2x(x - 1)(x + 1) Ta có BBT: Vậy với m=12 , thì min0; 2fx=f1 TM . Dựa vào BBT ta có: max[0;2]f(x)=f(2)=4. Tham khảo thêm một số tài liệu liên quan: Đề thi thử Toán 2024 phát triển từ đề tham khảo 500 Đề thi thử THPT Quốc gia 2024 môn Toán (cả nước, có lời giải)

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Cho hàm số f (x) = (m - 1)x⁴ - 2mx² + 1 với m là tham số thực. Nếu $\min_{[0; 3]} f (x) = f (2)$ thì $\max_{[0; 3]} f (x)$ bằng

A. $- \frac{13}{3};$

B. 4;

C. $- \frac{14}{3};$

D. 1.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = 2a. Góc giữa đường thẳng BC' và mặt phẳng (ACC'A') bằng 30°. Thể tích của khối lăng trụ đã cho bằng

Câu 2:

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |x⁴ - 2mx² + 64x| có đúng ba điểm cực trị

Câu 3:

Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng ba số nguyên b thỏa mãn (3^b - 3)(a.2^b - 18) < 0?

Câu 4:

Cho các số phức z₁, z₂, z₃ thỏa mãn |z₁| = |z₂| = 2|z₃| = 2 và 8(z₁ + z₂)z₃ = 3z₁z₂. Gọi A, B, C lần lượt là các điểm biểu diễn của z₁, z₂, z₃ trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng

Câu 5:

Cho khối lăng trụ có diện tích đáy là 3a² và chiều cao 2a. Thể tích khối lăng trụ đã cho bằng

Câu 6:

Với a là số thực dương tùy ý, $4 \log \sqrt{a}$ bằng

Câu 7:

Trong không gian Oxyz, cho điểm A(1; 2; -2). Gọi (P) là mặt phẳng chứa trục Ox sao cho khoảng cách từ A đến (P) lớn nhất. Phương trình của (P) là

Câu 8:

Cho hình nón có góc ở đỉnh là 120° và chiều cao bằng 4. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Tính diện tích của (S) bằng:

Câu 9:

Cho khối chóp S.ABC có chiều cao bằng 3, đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng

Câu 10:

Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là

Câu 11:

Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?

Câu 12:

Câu 13:

Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x² + y² + x - 3y bằng

Câu 14:

Cho hàm số $f (x) = 1 - \frac{1}{\cos^{2} 2 x}$ . Khẳng định nào dưới đây đúng?

Đề thi liên quan

Câu hỏi mới nhất