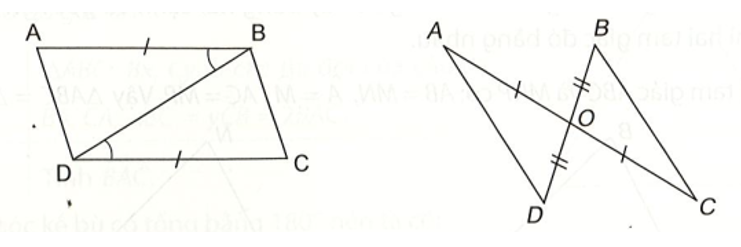
Cho hình vẽ dưới đây, biết rằng AC = BD, BC = AD, , .
Chứng minh rằng ∆ABC = ∆BDA.
 Giải bởi Vietjack
Giải bởi Vietjack
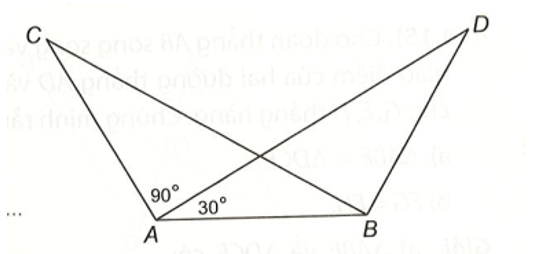
Theo hình vẽ, ta có:
Hai tam giác ABC và BAD, có:
AC = BD, BC = AD (theo giả thiết), AB là cạnh chung
Vậy ∆ABC = ∆BAD (c – c – c)
Từ đây suy ra ,
Do tổng ba góc trong tam giác ABC bằng 180° nên ta có:
Vì ∆ABC = ∆BAD nên
Hai tam giác ABC và BDA, có:
(theo chứng minh trên)
BC = AD (theo giả thiết)
(theo chứng minh trên)
Vậy ∆ABC = ∆BDA.
Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:
a)Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như hình bên.
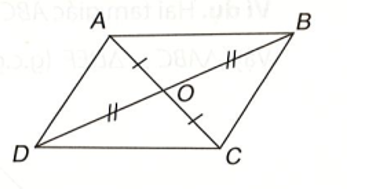
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.
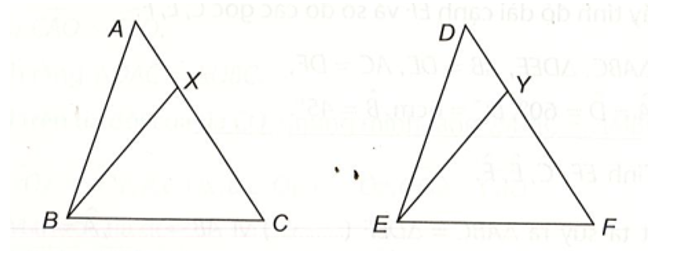
Cho tam giác ABC bằng tam giác DEF. Trên các cạnh AC và DF lấy các điểm X, Y sao cho AX = DY. Chứng minh .
Hai tam giác ABC và MNP bằng nhau khi và chỉ khi điều này dưới đây xảy ra?
A. AB = MN, AC = MP, ;
B. AB = MN, AC = MP, ;
C. AB = MP, AC = MN, ;
D. AB = AC, MN = MP, ;
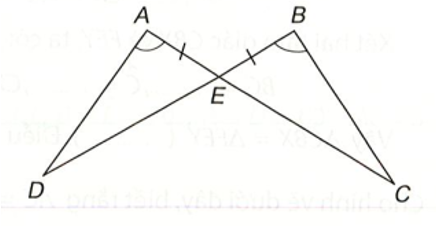
Chứng minh rằng hai tam giác ADE và BCE trong hình dưới đây bằng nhau.
Cho tam giác ABC. Câu nào dưới đây là đúng?
A. Góc A và góc C kề với cạnh AC;
B. Góc A xen giữa cạnh BA và CB;
C. Cạnh AC có một góc kề là góc B;
D. Góc B và C xen giữa cạnh BC.
Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Hai tam giác ABC và MNP bằng nhau khi và chỉ khi điều này dưới đây xảy ra?
A. BC = NP, , ;
B. BC = NP, , ;
C. BC = NP, , ;
D. BC = NP, , ;