Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi O là giao điểm của AC và BD.
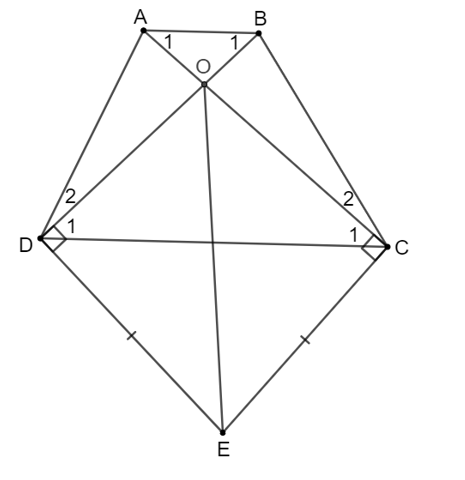
Xét ∆DOE và ∆COE có:
(vì OD ⊥ DE; OC ⊥ CE)
EC = ED (giả thiết)
Cạnh OE chung
Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).
Suy ra OC = OD (hai cạnh tương ứng).
Do đó tam giác OCD cân tại O nên .
Vì ABCD là hình thang nên AB // CD suy ra (cặp góc so le trong).
Do đó (vì ).
Suy ra tam giác OAB cân tại O nên OA = OB.
Xét ∆OAD và ∆OBC có:
OA = OB (chứng minh trên)
(hai góc đối đỉnh)
OC = OD (chứng minh trên)
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra (hai góc tương ứng).
Ta có .
Mà nên .
Hình thang ABCD có nên ABCD là hình thang cân.
Cách chứng minh hình thang cân
Chứng minh một hình thang là hình thang cân
Chứng minh hình thang có hai góc kề một đáy bằng nhau thì suy ra hình thang đó là hình thang cân.
Chứng minh hình thang có hai đường chéo bằng nhau thì suy ra hình thang đó là hình thang cân.
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Hình thang cân (Kết nối tri thức) | Lý thuyết Toán lớp 8
Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.
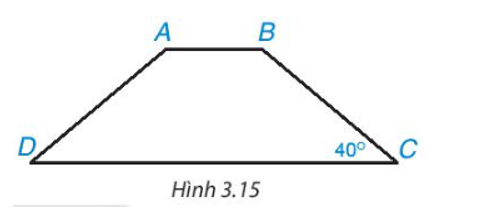
Tính các góc của hình thang cân ABCD (AB // CD), biết (H.3.15).
Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.
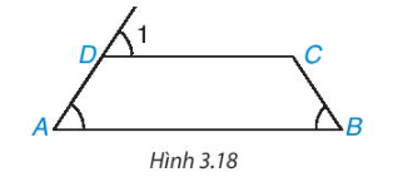
Cho tứ giác ABCD như Hình 3.18. Biết rằng . Chứng minh rằng AB = BC.
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
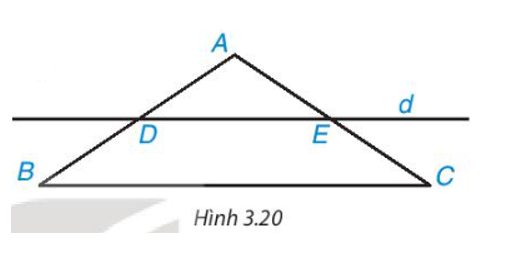
a) Tứ giác DECB là hình gì?
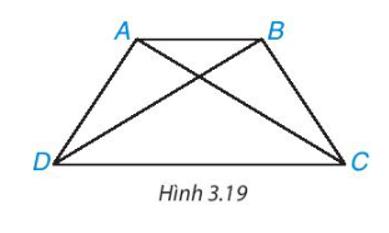
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
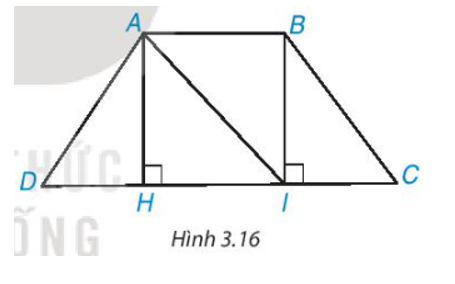
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
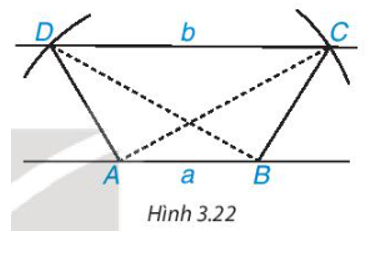
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.
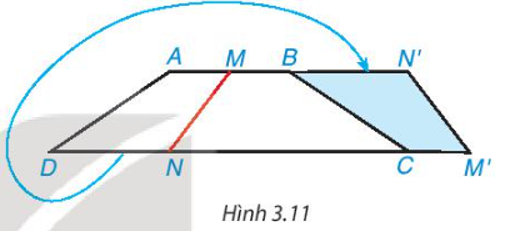
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
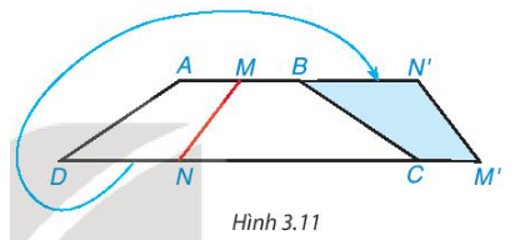
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.