A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
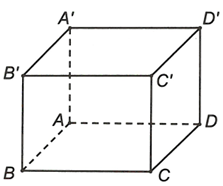
Ta có và
Mà suy ra sai
Phương pháp giải
Để chứng minh hai mặt phẳng song song ta có thể thực hiện theo một trong hai hướng sau:
- Chứng minh trong mặt phẳng này có hai đường thẳng cắt nhau cùng song song với mặt phẳng kia.
- Chứng minh hai mặt phẳng đó cùng song song với măt mặt phẳng thứ ba
Bài tập liên quan:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, AB = 8, SA = SB = 6. Gọi (P) là mặt phẳng đi qua O và song song với (SAB). Tính diện tích thiết diện của (P) và hình chóp S.ABCD.
A. 12
B.
C.
D. 13
Cách giải:
Đáp án B
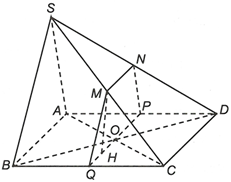
Qua O dựng đường thẳng PQ // AB
Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng PN // SA
Vậy N là trung điểm của SD.
Qua Q dựng đường thẳng QM // SB
Vậy M là trung điểm của SC. Nối M và N
=> thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì
Vậy tứ giác MNPQ là hình thang.
Ta có PQ
Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ.
Khi đó ta có
Vậy diện tích của thiết diện cần tìm là
Cách xác định thiết diện song song với đường thẳng: phương pháp giải và 20 bài tập
Cho hình chóp S.ABCD có đáy C là hình thang cân với cạnh bên hai đáy Mặt phẳng song song với và cắt cạnh SA tại M sao cho Diện tích thiết diện của và hình chóp S.ABCD bằng bao nhiêu?
Cho hình chóp S.ABCD với ABCD là hình thoi cạnh a, SAD là tam giác đều. Gọi M là một điểm thuộc cạnh AB, AM = x, (P) là mặt phẳng qua M song song với (SAD). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, AB = 8, SA = SB = 6. Gọi (P) là mặt phẳng đi qua O và song song với (SAB). Tính diện tích thiết diện của (P) và hình chóp S.ABCD.
Cho hình chóp cụt tam giác ABC.A'B'C' có hai đáy là hai tam giác vuông tại A và A' và có Khi đó tỉ số diện tích bằng bao nhiêu?