Cho hình chữ nhật ABCD. Trên cạnh AB lấy hai điểm M, N sao cho AM = NB < AB. Chứng minh tứ giác MNCD là hình thang cân.
 Giải bởi Vietjack
Giải bởi Vietjack
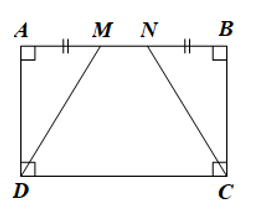

Phương pháp giải:
Bước 1: Chứng minh tứ giác MNCD là hình thang, dựa vào định nghĩa hình thang
Hình thang là tứ giác có hai cạnh đối song song.
Bước 2: Chứng minh hình thang MNCD là hình thang cân, dựa vào các dấu hiệu:
- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
Bài tập liên quan:
Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.
Cách giải:

Lý thuyết Toán 8 Bài 3: Hình thang cân
25 câu Trắc nghiệm Hình thang cân (Cánh diều) có đáp án - Toán lớp 8
Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.
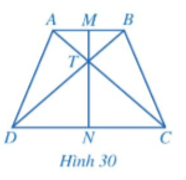
Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của AB, CD và T là giao điểm của AC và BD (Hình 30).
Chứng minh:
a) ;
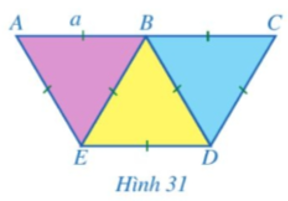
Người ta ghép ba hình tam giác đều có độ dài cạnh là a với vị trí như Hình 31.
a) Chứng minh ba điểm A, B, C thẳng hàng.
Hình 33a là mặt cắt đứng phần chứa nước của một con mương (Hình 32) khi đầy nước có dạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC), H là hình chiếu của D trên đường thẳng AC
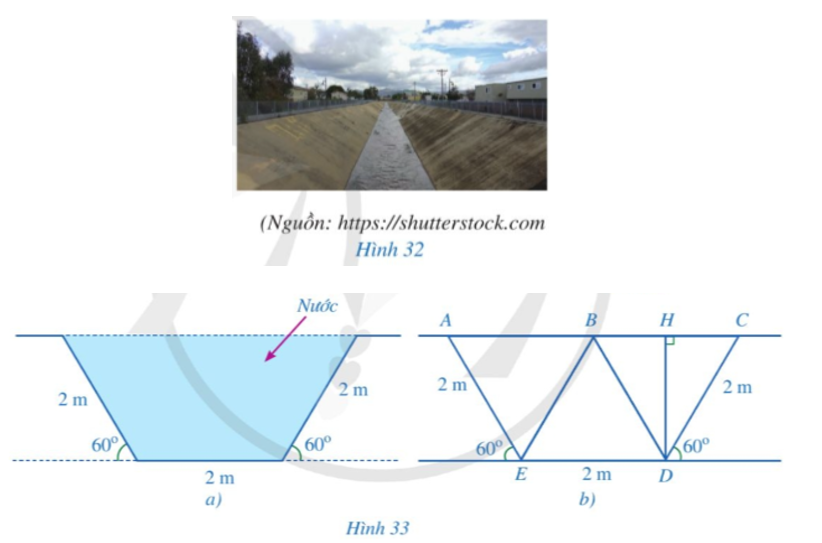
a) Chứng minh các tam giác BCD, BDE, ABE là các tam giác đều.
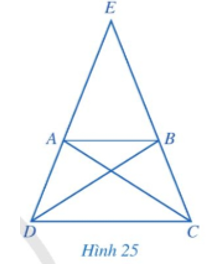
Cho hình thang cân ABCD có AB // CD, AB < CD, E là giao điểm của AD và BC (Hình 25).
a) So sánh các cặp góc: và ; và .
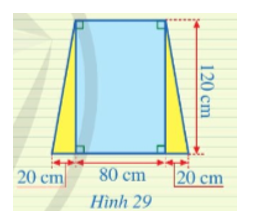
Một ô cửa sổ có dạng hình chữ nhật với chiều dài là 120 cm và chiều rộng là 80 cm. Người ta mở rộng ô cửa sổ đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô cửa sổ đó có dạng hình gì? Tính diện tích của ô cửa sổ đó sau khi mở rộng.
c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước.
b) So sánh các cặp đoạn thẳng: EA và EB; ED và EC. Từ đó, hãy so sánh AD và BC.
c) Hai tam giác ACD và BDC có bằng nhau hay không? Từ đó, hãy so sánh và .