Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên SA vuông với đáy, góc . Tính khoảng cách d giữa hai đường thẳng AB và SO.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
|
Ta có , suy ra Lại có , suy ra đều cạnh Tam giác vuông SAB, có Gọi E là trung điểm AD, suy ra và Do đó |
|
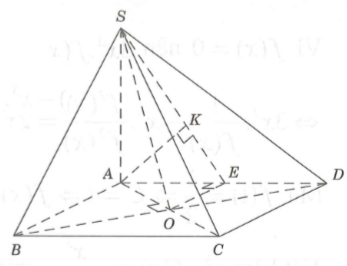
Kẻ
Khi đó
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm Một véctơ pháp tuyến của mặt phẳng (ABC) là:
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng và . Phương trình tham số của đường thẳng d là
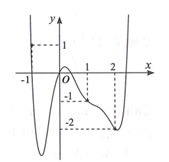
![Cho hàm số y=f(x) liên tục trên đoạn [-1;2] và có đồ thị như hình vẽ bên. Gọi M , n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [-1;2] . Ta có 2M+n bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/xas-1653213141.png)
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với và . Gọi S là tập hợp tất cả các điểm nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm . Xác suất để bằng
Trong không gian với hệ tọa độ Oxyz, cho hai điểm . Điểm M trong không gian thỏa mãn Khi đó độ dài OM lớn nhất bằng
Có bao nhiêu giá trị nguyên của tham số m để giá trị nhỏ nhất của hàm số trên đoạn đạt giá trị nhỏ nhất.