Cho hai đường thẳng:
d: và
Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và đến (P) là bằng nhau.
 Giải bởi Vietjack
Giải bởi Vietjack
Đường thẳng d đi qua M(6; 0 ;7) có vecto chỉ phương (0; −2; 1). Đường thẳng d1 đi qua N(-2; -2; -11) có vecto chỉ phương (1; 0; −1).
Do d và chéo nhau nên (P) là mặt phẳng đi qua trung điểm của đoạn vuông góc chung AB của d, và song song với d và .
Để tìm tọa độ của A, B ta làm như sau:
Lấy điểm A(6; - 2t; 7 + t) thuộc d, B( -2 + t’; -2; -11 – t’) thuộc . Khi đó: = (−8 + t′; −2 + 2t; −18 – t − t′)
Ta có:
Suy ra A(6; 4; 5), B(-6; -2; -7)
Trung điểm của AB là I(0; 1; -1)
Ta có: = (−12; −6; −12). Chọn = (2; 1; 2)
Phương trình của (P) là: 2x + (y – 1) + 2(z + 1) = 0 hay 2x + y + 2z + 1 = 0.
Có thể tìm tọa độ của A, B bằng cách khác:
Ta có: Vecto chỉ phương của đường vuông góc chung của d và là:
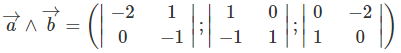
Gọi (Q) là mặt phẳng chứa d và đường vuông góc chung AB.
Khi đó:
Phương trình của (Q) là : –5(x – 6) + 2y + 4(z – 7) = 0 hay –5x + 2y + 4z + 2 = 0
Để tìm (Q) ta thế phương trình của vào phương trình của (Q). Ta có:
–5(–2 + t′) + 2(–2) + 4(–11 – t′) + 2 = 0
⇒ t′ = 4
⇒ (Q) = B(−6; −2; −7)
Tương tự, gọi (R) là mặt phẳng chứa và đường vuông góc chung AB. Khi đó: = (−1; 4; −1)
Phương trình của (R) là –x + 4y – z – 5 = 0.
Suy ra d (R) = A(6; 4; 5).
Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng
(): 2x + y + 2z + 1 = 0 và (): 2x + y + 2z + 5 = 0.
Trong không gian Oxyz, cho điểm A(-4; -2; 4) và đường thẳng d:
Viết phương trình đường thẳng đi qua A , cắt và vuông góc với đường thẳng d.
Cho mặt phẳng (P) : x + 2y – 2z + 3 = 0
và đường thẳng d:
Lập phương trình đường thẳng d’ là hình chiếu vuông góc của d lên mặt phẳng (P).
Cho hai mặt phẳng:
(): 2x + y + 2z + 1 = 0 và (): 4x – 2y – 4z + 7 = 0.
Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến () và () là bằng nhau.
Cho hình lập phương ABCD. có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của các cạnh B, CD. . Tính khoảng cách và góc giữa hai đường thẳng MP và N.
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và song song với mặt phẳng (Q): x – z = 0.
Lập phương trình mặt phẳng (P) chứa đường thẳng d: và song song với
Lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng: d:
Trong không gian Oxyz, cho hai điểm A(2; 0; 0), B(0; 0; 8) và điểm C sao cho = (0; 6; 0). Tính khoảng cách từ trung điểm I của BC đến đường thẳng OA.
Lập phương trình tham số của đường thẳng d đi qua điểm và song song với hai mặt phẳng cắt nhau
(P) Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với hai mặt phẳng (Q): 2x – y + 3z + 1 = 0 và (R): x – 2y – z + 8 = 0
Lập phương trình tham số của đường thẳng d đi qua hai điểm phân biệt và
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với đường thẳng d: