Biểu thức P = y – x, với x và y thỏa mãn hệ bất phương trình đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b. Hãy chọn kết quả đúng trong các kết quả sau:
A. và b = – 2;
B. a = 2 và ;
C. a = 3 và b = 0 ;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta vẽ đường thẳng d1: 2x + 3y – 6 = 0, đường thẳng d1 đi qua hai điểm (0; 2) và (3; 0)
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 + 3.0 – 6 = - 6 < 0, điểm O(0; 0) thoả mãn bất phương trình 2x + 3y – 6 ≤ 0, vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d1 và chứa điểm O(0; 0) (kể cả bờ).
Ta vẽ đường thẳng d2: 2x – 3y – 1 = 0, đường thẳng d2 đi qua hai điểm và
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 – 3.0 – 1 = - 1 < 0, điểm O(0; 0) thoả mãn bất phương trình 2x – 3y – 1 ≤ 0, vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d2 và chứa điểm O(0; 0) (kể cả bờ).
x0 có miền nghiệm là nửa mặt phẳng nằm bên phải trục tung (kể cả trục tung).
Miền nghiệm là phần không bị gạch trong hình dưới đây (kể cả bờ).
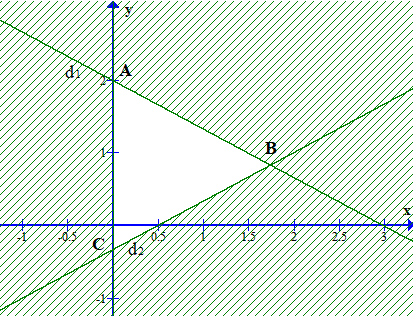
Miền nghiệm là hình tam giác ABC (kể cả biên), với A(0; 2);, .
Ta có
P(x; y) = y – x suy ra P(0; 2) = 2 – 0 = 2;
P(x; y) = y – x suy ra P = ,
P(x; y) = y – x suy ra P =
Vậy giá trị lớn nhất của P là a = 2 và giá trị nhỏ nhất của P là .
Phương pháp giải:
- Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng: trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0; x và y là các ẩn số.
- Để xác định miền nghiệm của bất phương trình , ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình như sau:
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng d:
Bước 2: Lấy điểm không thuộc d.
Bước 3: Tính và so sánh với 0.
Bước 4: Kết luận:
Nếu thì nửa mặt phẳng bờ d chứa điểm M là miền nghiệm của bất phương trình .
Nếu thì nửa mặt phẳng bờ d không chứa điểm M là miền nghiệm của bất phương trình .
Xem thêm một số kiến thức liên quan:
Lý thuyết Hệ bất phương trình bậc nhất hai ẩn (Cánh diều) hay, chi tiết | Toán lớp 10
Giá trị lớn nhất của biết thức F(x; y) = x + 2y với điều kiện là
Biểu thức F = y – x đạt giá trị nhỏ nhất với điều kiện tại điểm có toạ độ là
Giá trị nhỏ nhất của biểu thức F = y – x trên miền xác định bởi hệ là
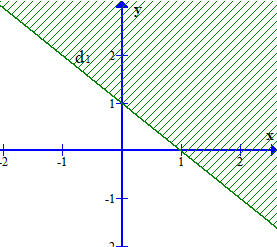
Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)?
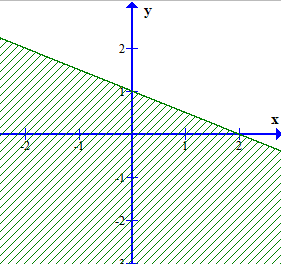
Phần nữa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình nào?
Giá trị nhỏ nhất của biểu thức F(x; y) = y – x trên miền xác định bởi hệ: là:
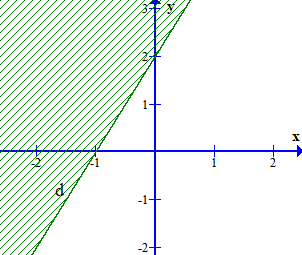
Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) trong hình dưới đây là miền nghiệm của bất phương trình nào?
Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình: 2x + y < 1?
Phần không bị gạch trong hình nào dưới đây biểu diễn miền nghiệm của hệ bất phương trình .
Phần không gạch chéo trong hình nào dưới đây biểu diễn miền nghiệm của bất phương trình 3x – 2y < – 6