Biểu thức F = y – x đạt giá trị nhỏ nhất với điều kiện tại điểm có toạ độ là
A. (4; 1);
C. ;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục tọa độ
Ta vẽ đường thẳng d1: – 2x + y = – 2, đường thẳng d1 đi qua hai điểm (0; – 2) và (1; 0)
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có – 2.0 + 0 = 0 > – 2, điểm O(0; 0) không thoả mãn bất phương trình – 2x + y ≤ – 2, vậy điểm O(0; 0) không thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d1 và không chứa điểm O(0; 0) (kể cả bờ).
Ta vẽ đường thẳng d2: x – 2y = 2, đường thẳng d2 đi qua hai điểm (0; – 1) và (2; 0)
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 – 2.0 = 0 < 2, điểm O(0; 0) thoả mãn bất phương trình x – 2y ≤ 2, vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d2 và chứa điểm O(0; 0) (kể cả bờ).
Ta vẽ đường thẳng d3: x + y = 5, đường thẳng d3 đi qua hai điểm (0; 5) và (5; 0)
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 + 0 = 0 < 5, điểm O(0; 0) thoả mãn bất phương trình x + y ≤ 5, vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d3 và chứa điểm O(0; 0) (kể cả bờ).
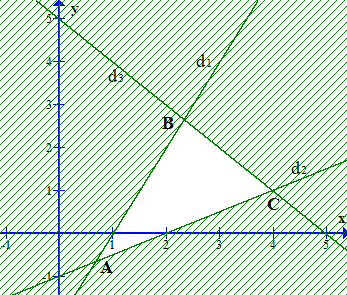
Miền nghiệm là phần không bị gạch trong hình dưới đây (kể cả bờ).
Nhận thấy biểu thức F = y – x chỉ đạt giá trị nhỏ nhất tại các điểm A, B hoặc C, với , , C(4;1).
Ta có
F(x; y) = y – x suy ra F = ,
F(x; y) = y – x suy ra F= ,
F(x; y) = y – x suy ra F(4;1).= 1 – 4 = – 3.
Vậy F = y – x đạt giá trị nhỏ nhất bằng – 3 tại điểm có toạ độ (4; 1).
Phương pháp giải:
Nhiều bài toán thực tế được đưa về bài toán tìm giá trị lớn nhất (nhỏ nhất) của biểu thức trên một miền đa giác – miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn.
Người ta chứng minh được F đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của đa giác.
+ Các bước giải
Bước 1: Đặt ẩn (hai ẩn x, y), từ giả thiết lập hệ bất phương trình bậc nhất hai ẩn.
Bước 2: Xác định miền đa giác nghiệm và tọa độ đỉnh của đa giác đó.
Bước 3: Tính gía trị cuả F tại các đỉnh của đa giác. So sánh các giá trị thu được.
Bước 4: Kết luận.
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Hệ bất phương trình bậc nhất hai ẩn (Kết nối tri thức) hay, chi tiết | Toán lớp 10
Trắc nghiệm Bất phương trình bậc nhất hai ẩn (Kết nối tri thức) có đáp án – Toán lớp 10
Giá trị lớn nhất của biết thức F(x; y) = x + 2y với điều kiện là
Giá trị nhỏ nhất của biểu thức F = y – x trên miền xác định bởi hệ là
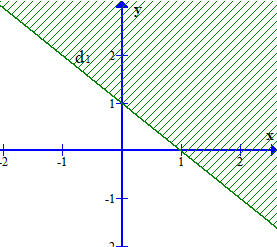
Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)?
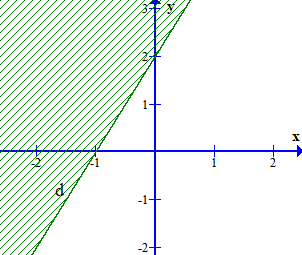
Phần nữa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình nào?
Biểu thức P = y – x, với x và y thỏa mãn hệ bất phương trình đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b. Hãy chọn kết quả đúng trong các kết quả sau:
Giá trị nhỏ nhất của biểu thức F(x; y) = y – x trên miền xác định bởi hệ: là:
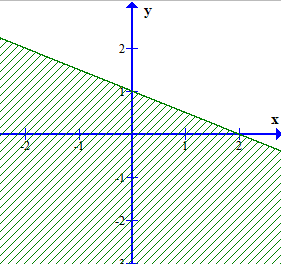
Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) trong hình dưới đây là miền nghiệm của bất phương trình nào?
Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình: 2x + y < 1?
Phần không bị gạch trong hình nào dưới đây biểu diễn miền nghiệm của hệ bất phương trình .
Phần không gạch chéo trong hình nào dưới đây biểu diễn miền nghiệm của bất phương trình 3x – 2y < – 6