Với giải Câu F89 trang 51 SBT Tin học lớp 10 Cánh diều chi tiết trong Bài 17, 18: Thực hành lập trình giải bài toán trên máy tính giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Tin học 10. Mời các bạn đón xem:

Giải SBT Tin học lớp 10 Bài 17, 18: Thực hành lập trình giải bài toán trên máy tính

Câu F89 trang 51 SBT Tin 10: Trung vị

Xét bài toán: Cho dãy số nguyên A = (a₁, a₂,…, a_n). Phần tử x của dãy được gọi là phần tử trung vị nếu nó lớn hơn hoặc bằng $\left[\frac{n}{2}\right]$ phần tử của dãy và nhỏ hơn hoặc bằng các phần tử còn lại trong dãy. Ví dụ, với A = (8, 1, 6, 3, 9, 2, 3, l, 7) trung vị là phần tử có giá trị là 5. Tìm và đưa ra giá trị của phần tử trung vị của dãy A bất kì.

Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu. Khi viết xong chương trình thì đề xuất ít nhất thêm hai bộ dữ liệu để kiểm thử chương trình.

Dữ liệu: Nhập vào từ thiết bị vào chuẩn một dòng chứa các phần tử của dãy, các số cách nhau một dấu cách.

Kết quả: Đưa ra thiết bị ra chuẩn giá trị của phần tử trung vị của dãy.

Ví dụ:

Trả lời:

Tóm tắt bài toán (Mô hình toán học)

Cho: Dãy A gồm n số nguyên.

Yêu cầu: Đưa ra phân tử trung vị (phần tử nằm ở giữa dãy đã sắp xếp).

Thuật toán và chọn kiểu dữ liệu cho các biến

- Bước 1. Nhập số nguyên n, nhập danh sách A chứa n số nguyên.

- Bước 2. Sắp xếp danh sách A.

- Bước 3. Đưa ra phần tử A [len (A) //2].

Tham khảo chương trình sau:

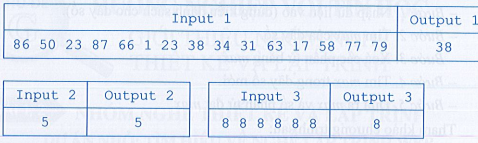
Ví dụ một số bộ dữ liệu để kiểm thử chương trình:

Xem thêm lời giải sách bài tập Tin học 10 Cánh diều hay, chi tiết khác:

Câu F86 trang 50 SBT Tin 10: Chia kẹo...

Câu F87 trang 50 SBT Tin 10: Điểm dừng xe...

Câu F88 trang 51 SBT Tin 10: Số bị thiếu...

Câu F90 trang 52 SBT Tin 10: Lớp II...

Xem thêm các bài giải SBT Tin học lớp 10 Cánh diều hay, chi tiết khác:

SBT Tin học 10 Bài 16: Kiểm thử và gỡ lỗi chương trình

SBT Tin học 10 Bài 17, 18: Thực hành lập trình giải bài toán trên máy tính

Lý thuyết Tin học 10 Bài 18: Lập trình giải quyết bài toán trên máy tính

SBT Tin học 10 Bài 1, 2: Nhóm nghề thiết kế và lập trình - Dự án nhỏ: Tìm hiểu về nghề lập trình web, lập trình trò chơi và lập trình cho thiết bị di động

SBT Tin học 10 Bài 1, 2: Hệ nhị phân và ứng dụng - Thực hành về các phép toán bit và hệ nhị phân