Với tóm tắt lý thuyết Toán lớp 6 Bài 9: Dấu hiệu chia hết sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 9: Dấu hiệu chia hết

Video giải Toán 6 Bài 9: Dấu hiệu chia hết - Kết nối tri thức

A. Lý thuyết Dấu hiệu chia hết

1. Dấu hiệu chia hết cho 2, cho 5

Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

Ví dụ 1. Cho các số sau: 242; 102; 255; 76; 8 090; 260; 145.

a) Các số chia hết cho 2;

b) Các số chia hết cho 5;

c) Các số chia hết cho cả 2 và 5.

Lời giải

a) Các số chia hết cho 2 là các số có chữ số tận cùng là . 

Do đó trong các số trên các số chia hết cho 2 là: 242; 102; 76; 8 090; 260.

b) Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.

Do đó trong các số trên số chia hết cho 5 là: 255; 8 090; 260; 145.

c) Các số chia hết cho cả 2 và 5 là: 8 090; 260.

2. Dấu hiệu chia hết cho 9, cho 3

Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

Chú ý: Các số chia hết cho 9 thì chia hết cho 3 nhưng chia hết cho 3 chưa chắc chia hết cho 9.

Ví dụ 2. Trong các số sau: 1 954; 264; 315; 705; 2 231; 3 771 số nào chia hết cho 3, số nào chia hết cho 9.

Lời giải

+) Ta có: 1 + 9 + 5 + 4 = 19 không chia hết cho 9 cũng không chia hết cho 3 nên 1954 không chia hết cho 3 và 9.

+) Ta có: 2 + 6 + 4 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 264 chia hết cho 3 và không chia hết cho 9.

+) Ta có: 3 + 1 + 5 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 315 vừa chia hết cho 3 vừa chia hết cho 9.

+) Ta có 7 + 0 + 5 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 705 chia hết cho 3 và không chia hết cho 9.

+) Ta có 2 + 2 + 3 + 1 = 8 không chia hết cho 3 cũng không chia hết cho 9 nên 2 231 không chia hết cho 3 cũng không chia hết cho 9.

+) Ta có: 3 + 7 + 7 + 1 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 3771 vừa chia hết cho 3 vừa chia hết cho 9.

Vậy các số chia hết cho 3 là 264; 315; 705; 3 771; các số chia hết cho 9 là 315; 3 771.

B. Bài tập Dấu hiệu chia hết

Bài 1. Khối lớp 6 của một trường có 396 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô chia nhóm được như vậy không?

Lời giải

Muốn chia đều số học sinh của khối 6 thành 9 nhóm thì 396 phải chia hết cho 9.

Ta có: 3 + 9 + 6 = 12 + 6 = 18 chia hết cho 9 nên 396 chia hết cho 9.

Do đó cô hoàn toàn có thể chia số học sinh khối 6 thành 9 nhóm.

Bài 2. Thay dấu * bởi một chữ số để số   :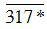

a) Chia hết cho 2;

b) Chia hết cho 3;

c) Chia hết cho 5;

d) Chia hết cho 9.

Lời giải

a) Để số đã cho chia hết cho 2 thì * ∈ .

Vậy để số đã cho chia hết cho 2 thì * có thể thay thế bằng các chữ số .

b) Ta có: 3 + 1 + 7 + * = 11 + * 

Để số đã cho chia hết cho 3 thì 11 + * chia hết cho 3, 

Mà * thuộc

Từ đó, Ta có: 11 + 1 =12 chia hết cho 3;

11 + 4 = 15 chia hết cho 3;

11 + 7 = 18 chia hết cho 3

nghĩa là * ∈ .

Vậy để số đã cho chia hết cho 3 thì * có thể thay thế bằng các chữ số .

c) Để số đã cho chia hết cho 5 thì * ∈ .

Vậy để số đã cho chia hết cho 5 thì có thể thay thế * bằng các chữ số .

d) Ta có: 3 + 1 + 7 + * = 11 + * 

Để số đã cho chia hết cho 9 thì 11 + * chia hết cho 9

Mà * thuộc

Từ đó, ta có:

11 + 7 = 18 chia hết cho 9.

Vậy để số đã cho chia hết cho 9 ta có thể thay thế * bằng số 7.

Bài giảng Toán 6 Bài 9: Dấu hiệu chia hết - Kết nối tri thức

Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 8: Quan hệ chia hết và tính chất

Lý thuyết Bài 9: Quan hệ chia hết và tính chất

Lý thuyết Bài 10: Số nguyên tố

Lý thuyết Bài 11: Ước chung. Ước chung lớn nhất

Lý thuyết Bài 12: Bội chung. Bội chung nhỏ nhất