Tailieumoi.vn xin giới thiệu đề thi học sinh giỏi Toán lớp 9 cấp thành phố năm 2023 - 2024 phòng GD&ĐT Sông Công tỉnh Thái Nguyên có lời giải chi tiết. Hi vọng với bộ tài liệu này các em ôn luyện, củng cố kiến thức, rèn luyện kĩ năng làm bài thật tốt để bước bài kì thi HSG sắp tới.
Đề thi HSG Toán 9 cấp thành phố năm 2023 - 2024 phòng GD&ĐT Sông Công - Thái Nguyên
Một số câu hỏi có trong đề thi:
+ Cho phương trình x2 – (2m + 3)x + m = 0 (với m là tham số).
a. Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của m.
b. Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 sao cho (x12 + x22) đạt giá trị nhỏ nhất.
+ Tìm tất cả các số nguyên dương n sao cho n4 + 4n là số nguyên tố. Tìm nghiệm nguyên của phương trình 20y2 – 6xy + 15x = 150.
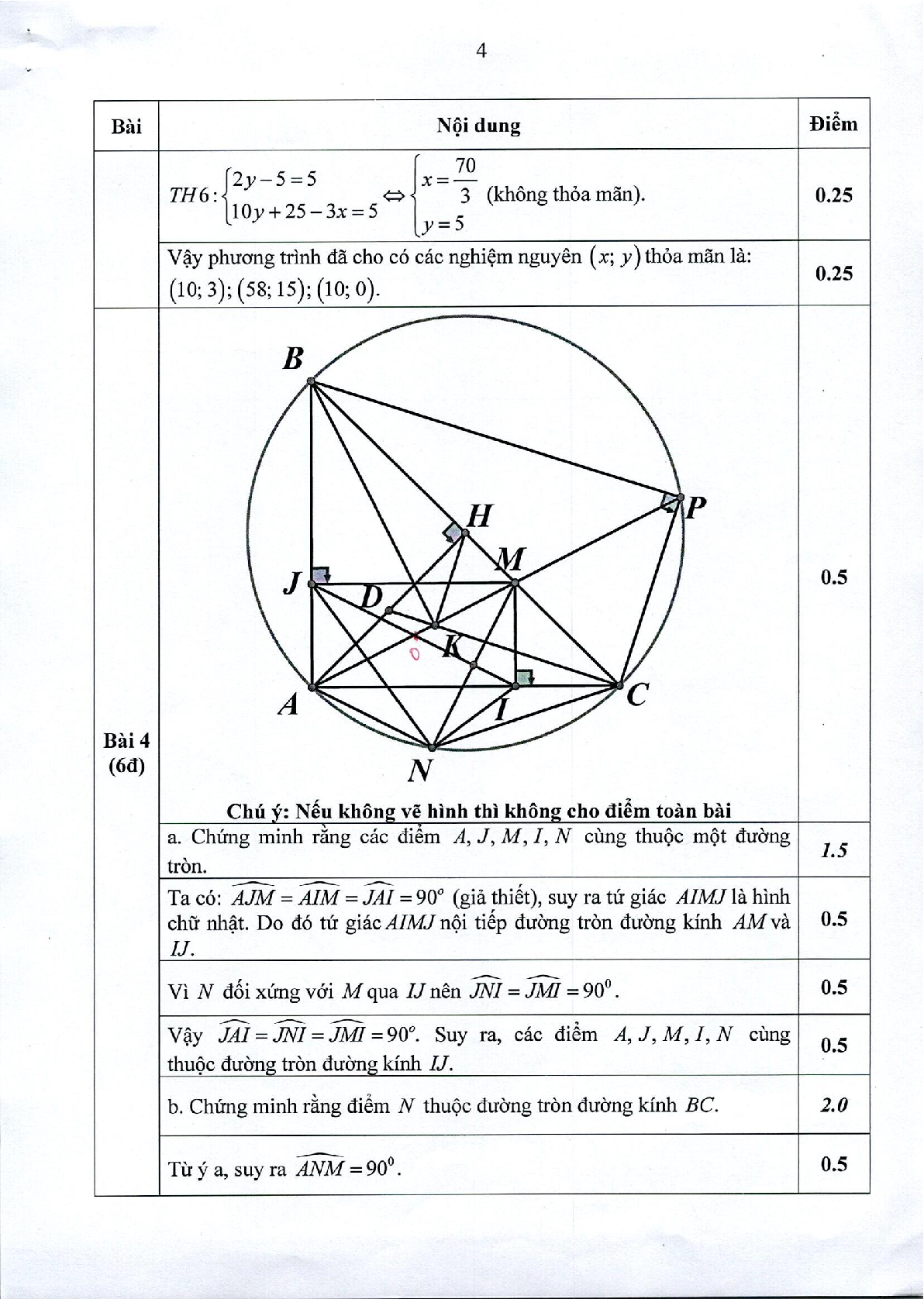
+ Cho tam giác ABC vuông cân tại A có AH là đường cao. Trên đoạn thẳng HC lấy điểm M (M H M C). Gọi I, J lần lượt là chân đường vuông góc kẻ từ M đến các cạnh AC và AB; N là điểm đối xứng của M qua đường thẳng IJ.
a. Chứng minh rằng các điểm A, J, M, I, N cùng thuộc một đường tròn.
b. Chứng minh rằng điểm N thuộc đường tròn đường kính BC.
c. Đường thẳng AM cắt đường tròn đường kính BC tại điểm P (P khác A). Chứng minh rằng PM PM AB PC PB.
d. Gọi D là trung điểm của đoạn thẳng AH. Kẻ HK vuông góc với CD tại điểm K. Chứng minh rằng BAK = KHC.
Để xem đầy đủ đề thi và lời giải chi tiết mời bạn đọc tải tài liệu về.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
