Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 2 môn Toán lớp 7 sách Cánh diều năm 2024 – 2025. Tài liệu gồm 2 đề thi được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 2 Toán 7. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 2 Toán 7 Cánh diều bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi giữa kì 2 Toán lớp 7 Cánh diều có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Cánh diều
Năm học ..................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:
|
Loại nước uống |
Nước cam |
Nước dứa |
Nước chanh |
Nước ổi |
|
Số người chọn |
|
|
|
|
Loại nước nào ít người ưa chuộng nhất?
A. Nước cam B. Nước dứa C. Nước chanh D. Nước ổi
Câu 2. Biểu thức đại số biểu thị bình phương của một tổng hai số và là:
A. B. C. D.
Câu 3. Giá trị của biểu thức: tại là:
A. B. C. D.
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. B. C. D.
Câu 5. Sắp xếp các hạng tử của đa thức theo lũy thừa giảm dần của biến ta được:
A. B.
C. D.
Câu 6. Cho tam giác có . Độ dài cạnh là một số nguyên (cm). Độ dài cạnh là:
A. B. C. D.
Câu 7. Cho tam giác , có . Khi đó quan hệ giữa ba cạnh là:
A. B. C. D.
Câu 8. Giao điểm của 3 đường trung trực của tam giác
A. cách đều 3 cạnh của tam giác.
B. được gọi là trực tâm của tam giác.
C. cách đều 3 đỉnh của tam giác.
D. cách đỉnh một đoạn bằng độ dài đường trung tuyến đi qua đỉnh đó.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Biểu đồ hình quạt tròn bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) lực lượng lao động (từ 15 tuổi trở lên) phân theo trình độ chuyên môn kĩ thuật (CMKT) của nước ta (năm 2020).
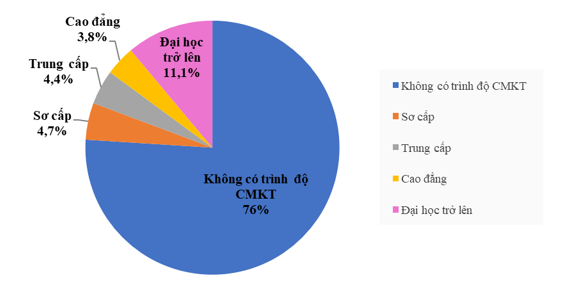
a) Trong năm 2020, có bao nhiêu phần trăm lực lượng lao động không có trình độ CMKT? Trình độ sơ cấp? Trình độ trung cấp? Trình độ cao đẳng? Trình độ đại học trở lên?
b) Trong năm 2020, lực lượng lao động không có trình độ CMKT gấp bao nhiêu lần lực lượng lao động có trình độ đại học trở lên (làm tròn đến hàng đơn vị)?
c) Số lao động có trình độ đại học trở lên năm 2020 là bao nhiêu triệu người, biết có 54,6 triệu người từ 15 tuổi trở lên thuộc lực lượng lao động của cả nước trong năm 2020 (làm tròn kết quả đến hàng phần trăm)?
Bài 3. (2 điểm) Cho hai đa thức: và .
a) Thu gọn và sắp xếp hai đa thức và theo lũy thừa giảm dần của biến.
b) Tính và tìm nghiệm của đa thức .
Bài 4. (3,5 điểm) Cho tam giác cân tại , kẻ vuông góc với . Gọi là trung điểm của . Trên tia đối của tia lấy điểm sao cho .
a) Chứng minh rằng: và vuông góc với.
b) Chứng minh rằng: từ đó suy ra .
c) Chứng minh rằng:
d) Gọi là trung điểm của . Chứng minh rằng ba điểm thẳng hàng.
Bài 5. (0,5 điểm) Cho các số thực thỏa mãn: .
Chứng minh rằng: .
(Giả thiết các tỉ số đều có nghĩa)
Hướng dẫn giải:
I. Trắc nghiệm
|
1.B |
2. D |
3. A |
4. C |
|
5. A |
6. D |
7. D |
8. C |
Câu 1.
Phương pháp:
Đọc và miêu tả dữ liệu từ bảng thống kê.
Cách giải:
Loại nước ít người ưa chuộng nhất là nước dứa.
Chọn B.
Câu 2.
Phương pháp:
Dùng các chữ, các số và các phép toán để diễn đạt các mệnh đề phát biểu bằng lời.
Cách giải:
Bình phương của một tổng hai số và là:
Chọn D.
Câu 3.
Phương pháp:
Thay vào biểu thức để tính.
Cách giải:
Thay vào biểu thức ta có:
Chọn A.
Câu 4.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: không là một đơn thức.
Chọn C.
Câu 5.
Phương pháp:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến:
Chọn A.
Câu 6.
Phương pháp:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là nếu .
+ Trong trường hợp xác định được là số lớn nhất trong ba số thì điều kiện tồn tại tam giác là .
Cách giải:
Xét tam giác , ta có:
Vì độ dài cạnh là một số nguyên nên
Chọn D.
Câu 7.
Phương pháp:
Sử dụng quan hệ giữa góc và cạnh đối diện trong tam giác.
Cách giải:
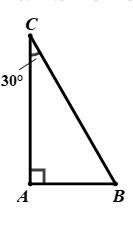
Xét có: (định lý tổng ba góc trong một tam giác)
Ta có: (vì )
(quan hệ giữa góc và cạnh đối diện trong tam giác)
Chọn D.
Câu 8.
Phương pháp
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp:
a) Đọc và mô tả biểu đồ hình quạt tròn.
b) Thực hiện phép chia.
c) Số lao động có trình độ đại học trở lên năm 2020 = % tương ứng . số người lao động.
Cách giải:
a) Trong năm 2020, có:
+ 76% lực lượng lao động không có trình độ CMKT;
+ 4,7% lực lượng lao động có trình độ sơ cấp;
+ 4,4 % lực lượng lao động có trình độ trung cấp;
+ 3,8% lực lượng lao động có trình độ cao đẳng;
+ 11,1% lực lượng lao động có trình độ đại học trở lên.
b) Từ biểu đồ hình quạt tròn, ta thấy 76% lực lượng lao động không có trình độ CMKT; 11,1% lực lượng lao động có trình độ đại học trở lên.
Ta có:
Vậy lực lượng lao động không có trình độ CMKT gấp 7 lần lực lượng lao động có trình độ đại học trở lên.
c) Số lao động có trình độ đại học trở lên năm 2020 là: (triệu người)
Bài 2.
Phương pháp:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức , ta giải phương trình
Cách giải:
a)
b)
Ta có:
Vậy là nghiệm của đa thức
Bài 3.
Phương pháp:
+ Sử dụng các cách chứng minh hai tam giác bằng nhau.
+ Mối quan hệ giữa góc và cạnh trong tam giác (Cạnh đối diện với góc lớn hơn thì lớn hơn)
+ Tính chất trọng tâm của tam giác.
Cách giải:
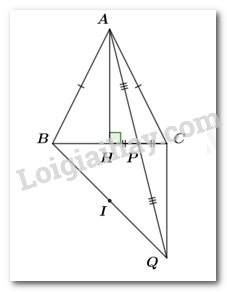
a. Xét và có:
+ (gt)
+ (đối đỉnh)
+ (gt)
(c.g.c) (đpcm).
(hai góc tương ứng)
(đpcm).
b. Theo (a)
(hai cạnh tương ứng) (1)
Mà vuông tại H (cạnh góc vuông <cạnh huyền) (2)
Từ (1) và (2), suy ra (đpcm).
c. Xét có (3) (Mối quan hệ giữa cạnh- góc trong tam giác)
Mặt khác (4)
Từ (3) và (4) hay (đpcm).
d. Xét có là trung tuyến ứng với cạnh
Mà (do là trung điểm của , là trung điểm của ) là trọng tâm (5)
Lại có là trung điểm của là trung tuyến ứng với cạnh (6)
Từ (5), (6)
thẳng hàng (đpcm)
Bài 4.
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: nên
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Mà và (gt) nên (đpcm)
Ma trận đề kiểm tra giữa kì II
Môn: Toán – Lớp 7 – Thời gian làm bài: 90 phút
|
STT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Tổng % điểm |
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||||||
|
TN |
TL |
TN |
TL |
TN |
TL |
TN |
TL |
||||
|
1 |
Một số yếu tố thống kê và xác suất |
Một số yếu tố thống kê |
4 |
|
|
2 |
|
|
|
2 |
55% |
|
Một số yếu tố xác suất |
1 |
|
1 |
|
|
1 |
|
|
|||
|
2 |
Tam giác |
Tổng các góc của một tam giác. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác |
2 |
|
|
|
|
|
|
|
45% |
|
Hai tam giác bằng nhau. Ba trường hợp bằng nhau của tam giác |
3 |
|
1 |
2 |
|
1 |
|
|
|
||
|
Tổng: Số câu Điểm |
10 (2,5đ) |
|
2 (0,5đ) |
4 (4,0đ) |
|
2 (2,0đ) |
|
2 (1,0đ) |
20 10 |
||
|
Tỉ lệ |
25% |
45% |
20% |
10% |
100% |
||||||
|
Tỉ lệ chung |
70% |
30% |
100% |
||||||||
Lưu ý:
− Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ II TOÁN – LỚP 7
|
STT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Số câu hỏi theo mức độ |
|||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
1 |
Một số yếu tố thống kê và xác suất |
Một số yếu tố thống kê |
Nhận biết: - Nhận biết được những dạng biểu diễn khác nhau cho một tập dữ liệu. - Nhận biết tính đại diện, tính hợp lí của dữ liệu. - Đọc các dữ liệu biểu diễn trên biểu đồ. - Phân loại dữ liệu. |
4TN |
|
|
|
|
Thông hiểu: - Giải thích tính hợp lí của các dữ liệu theo các tiêu chí toán học đơn giản (tính hợp lí, tính đại diện của một kết luận trong phỏng vấn; tính hợp lí của các quảng cáo,...). - Mô tả và phân tích được các dữ liệu ở dạng biểu đồ thống kê: biểu đồ hình quạt tròn, biểu đồ đoạn thẳng. |
|
2TL |
|
|
|||
|
Vận dụng cao: - Tính toán, so sánh, mối liên hệ thống kê với kiến thức các môn học khác và trong thực tiễn (môi trường, y học, tài chính,...). - Giải quyết được những vấn đề đơn giản liên quan đến các số liệu thu được ở dạng: biểu đồ hình quạt tròn; biểu đồ đoạn thẳng. - Đưa ra một số nhận xét, biện pháp giải quyết trong thực tế. |
|
|
|
2TL |
|||
|
Một số yếu tố xác suất |
Nhận biết: - Nhận biết số kết quả xảy ra của mỗi biến cố. - Nhận biết sự kiện là biến cố ngẫu nhiên trong một số trò chơi đơn giản. |
1TN |
|
|
|
||
|
Thông hiểu: - Tìm số kết quả thuận lợi dựa vào dữ kiện đã cho. - Tính xác suất của một số biến cố trong một số trò chơi đơn giản. |
|
1TN 1TL |
|
|
|||
|
Vận dụng: Tính xác suất của một số biến cố ngẫu nhiên trong một số bài toán thực tế. |
|
|
1TL |
|
|||
|
|
Tam giác
|
Tổng các góc của một tam giác. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác |
Nhận biết: - Nhận biết định lí tổng các góc trong một tam giác và trong tam giác vuông. - Nhận diện loại tam giác dựa vào các góc. - Khái niệm khái niệm hai tam giác bằng nhau. - Nhận biết liên hệ độ dài ba cạnh trong một tam giác. - Nhận biết điều kiện để hai tam giác bằng nhau. |
2TN |
|
|
|
|
Hai tam giác bằng nhau. Ba trường hợp bằng nhau của tam giác |
Nhận biết: - Nhận biết hai tam giác bằng nhau. - Nhận biết điều kiện để hai tam giác bằng nhau theo các trường hợp cho trước. |
3TN |
|
|
|
||
|
Thông hiểu: - Chứng minh hai tam giác bằng nhau theo ba trường hợp. - Tìm số đo của góc, độ dài của cạnh trong tam giác. - Chứng minh hai cạnh, hai góc bằng nhau. |
|
1TN 2TL |
|
|
|||
|
Vận dụng: Chứng minh hai đường thẳng song song, hai đường thẳng vuông góc dựa vào các điều kiện về cạnh và góc. |
|
|
1TL |
||||
Đề thi giữa kì 2 Toán lớp 7 Cánh diều có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Cánh diều
Năm học ..................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 2)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Dữ liệu thống kê là số còn được gọi là
A. số liệu;
B. dữ liệu;
C. con số;
D. Cả A, B và C đều sai.
Câu 2. Cho biểu đồ dưới đây
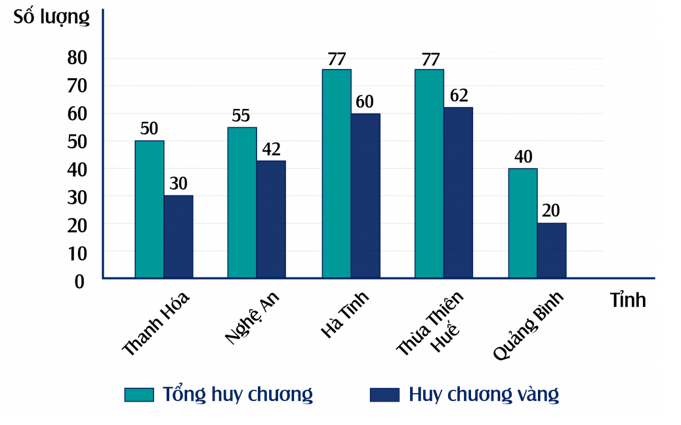
Đối tượng thống kê là
A. Số lượng huy chương;
B. Số lượng huy chương vàng;
C. Các tỉnh: Thanh Hóa, Nghệ An, Hà Tĩnh, Thừa Thiên Huế, Quảng Bình;
D. Cả A, B và C đều sai.
Câu 3. Cho biểu đồ đoạn thẳng như hình vẽ.
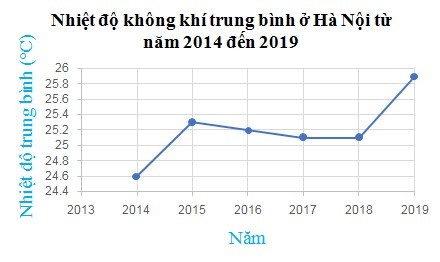
Biểu đồ trên có 6 điểm và mỗi điểm được xác định bởi
A. năm thống kê;
B. năm thống kê và nhiệt độ không khí trung bình ở Hà Nội vào năm đó;
C. nhiệt độ không khí trung bình ở Hà Nội;
D. Cả A, B và C đều sai.
Câu 4. Cho biểu đồ sau.
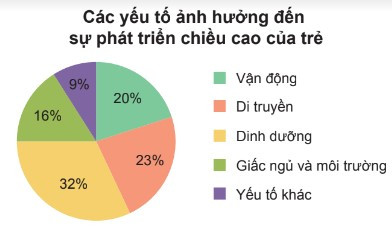
Trong biểu đồ trên, yếu tố ảnh hưởng đến 23% sự phát triển chiều cao của trẻ là
A. Vận động;
B. Giấc ngủ và môi trường;
C. Dinh dưỡng;
D. Di truyền.
Câu 5. Xác suất của biến cố trong trò chơi gieo xúc xắc bằng
A. tích của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc;
B. tỉ số của số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc và số các kết quả thuận lợi cho biến cố;
C. hiệu của số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc và số các kết quả thuận lợi cho biến cố;
D. tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.
Câu 6. Vòng tứ kết cuộc thi bơi lội có sáu trường với 8 học sinh đại diện tham gia:
THCS Nguyễn Huệ: Kiệt;
THCS Nguyễn Khuyến: Long;
THCS Chu Văn An: Nguyên và Đăng;
THCS Nguyễn Bỉnh Khiêm: Minh;
THCS Lưu Văn Liệt: Thành;
THCS Nguyễn Du: Kha và Bình.
Xét biến cố “Người chiến thắng là học sinh đến từ trường THCS Nguyễn Huệ hoặc THCS Nguyễn Du”. Tính xác suất của biến cố trên.
A. ;
B. ;
C. ;
D. .
Câu 7. Cho các tam giác dưới đây (hình vẽ).
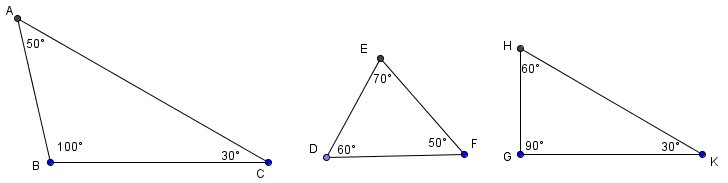
Tam giác tù là
A. Tam giác GHK;
B. Tam giác DEF;
C. Tam giác ABC;
D. Cả A và C.
Câu 8. Cho tam giác MNP có và . So sánh độ dài NP và MP là
A. NP > MP;
B. NP = MP;
C. NP < MP;
D. Không đủ điều kiện để so sánh.
Câu 9. Cho ∆ABC = ∆MNP. Trong các khẳng định sau đây khẳng định nào sai?
A. ;
B. BC = MP;
C. ;
D. AB = MN.
Câu 10. Cho tam giác ABC và tam giác MNP có AB = MP, AC = NM, BC = NP. Khẳng định nào dưới đây đúng?
A. ∆ABC = ∆MNP;
B. ∆ABC = ∆NMP;
C. ∆ABC = ∆PMN;
D. ∆ABC = ∆MPN.
Câu 11. Phát biểu đúng là
A. Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau;
B. Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và một góc của tam giác kia thì hai tam giác đó bằng nhau;
C. Nếu hai cạnh của tam giác này bằng hai cạnh của tam giác kia thì hai tam giác đó bằng nhau;
D. Nếu một góc của tam giác này bằng một góc của tam giác kia thì hai tam giác đó bằng nhau.
Câu 12. Cho hình vẽ sau, trong đó AB // CD, AB = CD.
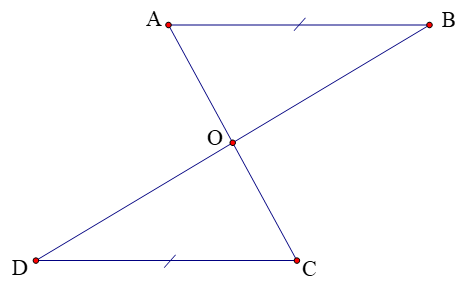
Khẳng định đúng là
A. OA = OD;
B. ;
C. O là trung điểm của AC;
D. ∆AOB = ∆DOC.
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm) Kết quả tìm hiểu về kết quả xếp loại học lực của các bạn học sinh khối 7 được cho bởi bảng thống kê sau:
|
Xếp loại học lực của học sinh khối 7 |
||||
|
Loại |
Giỏi |
Khá |
Trung bình |
Yếu |
|
Số học sinh |
120 |
285 |
150 |
25 |
a) Hãy phân loại các dữ liệu trong bảng thống kê trên dựa trên tiêu chí định tính và định lượng.
b) Dữ liệu trên có đại diện cho kết quả học tập của các bạn học sinh khối 7 hay không? Vì sao?
Bài 2. (1,0 điểm) Một nhóm du khách gồm 11 người đến từ các quốc gia: Anh; Pháp; Mỹ; Thái Lan; Bỉ; Ấn Độ; Hà Lan; Cu Ba; Nam Phi; Nhật Bản; Brasil. Chọn ngẫu nhiên một người trong nhóm du khách trên. Tính xác suất của biến cố “Du khách được chọn đến từ châu Âu”.
Bài 3. (3,0 điểm) Cho góc bẹt xOy có tia phân giác Ot. Trên tia Ot lấy hai điểm A, B (A nằm giữa O và B). Lấy điểm C ∈ Ox sao cho OC = OB, lấy điểm D ∈ Oy sao cho OD = OA.
a) Chứng minh AC = BD và AC ⊥ BD.
b) Gọi M, N lần lượt là trung điểm của AC và BD. Chứng minh OM = ON.
c) Tính các góc của tam giác MON.
Bài 4. (1,0 điểm) Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn lượng phát thải khí nhà kính trong ba lĩnh vực: Nông nghiệp, Năng lượng, Chất thải vào năm 2020 của Việt Nam (tính theo tỉ số phần trăm).
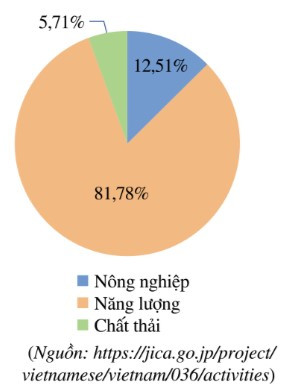
Dựa vào biểu đồ trên, hãy trả lời các câu hỏi sau:
a) Tính lượng khí nhà kính được tạo ra ở lĩnh vực Năng lượng và Chất thải của Việt Nam vào năm 2020. Biết rằng tổng lượng phát thải khí nhà kính trong ba lĩnh vực trên của Việt Nam vào năm 2020 là 466 triệu tấn khí cacbonic tương đương (tức là những khí nhà kính khác đều được quy đổi về khí cacbonic khi tính khối lượng).
b) Nêu hai biện pháp mà chính phủ Việt Nam đã đưa ra nhằm giảm lượng khí thải và giảm bớt tác động của khí nhà kính.
ĐÁP ÁN ĐỀ SỐ 2
I. Bảng đáp án trắc nghiệm
|
1. A |
2. C |
3. B |
4. D |
5. D |
6. B |
|
7. C |
8. A |
9. B |
10. D |
11. A |
12. C |
II. Hướng dẫn giải trắc nghiệm
Câu 4.
23% được ghi ở hình quạt tròn màu hồng. Mà hình quạt tròn đó biểu diễn yếu tố di truyền.
Do đó, yếu tố ảnh hưởng đến 23% sự phát triển chiều cao của trẻ là di truyền.
Câu 6.
Có 8 học sinh tham gia nên có 8 kết quả có thể xảy ra.
Trường THCS Nguyễn Huệ có 1 học sinh và THCS Nguyễn Du có 2 học sinh nên có 3 kết quả thuận lợi cho biến cố “Người chiến thắng là học sinh đến từ trường THCS Nguyễn Huệ hoặc THCS Nguyễn Du”.
Do đó xác suất của biến cố trên là: .
Câu 8.
Trong tam giác MNP có: và (giả thiết)
Nên
Do đó NP > MP.
Câu 9.
Ta có ∆ABC = ∆MNP (giả thiết)
Suy ra: AB = MN; BC = NP; AC = MP (các cạnh tương ứng bằng nhau)
; ; (các góc tương ứng bằng nhau)
Vậy BC = MP là khẳng định sai.
Câu 12.
Xét ∆AOB và ∆COD có:
(hai góc so le trong do AB // CD)
AB = CD (gt)
(hai góc so le trong do AB // CD)
Do đó, ∆AOB = ∆COD (g.c.g)
Suy ra OA = OC (hai cạnh tương ứng)
Do đó O là trung điểm của AC.
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm)
a) Dữ liệu định tính là: kết quả xếp loại học lực.
Dữ liệu định lượng là: số bạn học sinh tham gia xếp loại.
b) Dữ liệu trên đủ điều kiện đại diện được cho kết quả xếp loại học lực của học sinh khối 7 vì đối tượng khảo sát đã bao gồm tất cả các bạn học sinh là nam và nữ trong khối 7.
Bài 2. (1,0 điểm)
Có 11 du khách ứng với 11 quốc gia nên có 11 kết quả có thể xảy ra.
Các kết quả thuận lợi của biến cố “Du khách được chọn đến từ châu Âu” là: Anh; Pháp; Bỉ; Hà Lan. Có 4 kết quả thuận lợi.
Vì vậy, xác suất của biến cố trên là: .
Bài 3. (3,0 điểm)
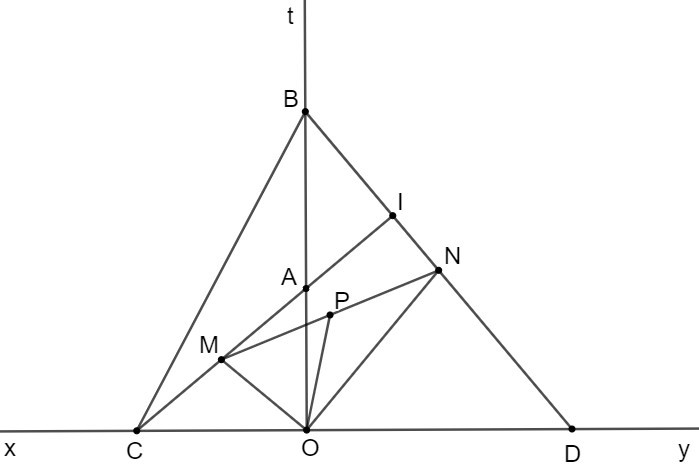
a) Vì góc xOy bẹt có Ot là tia phân giác nên Ot ⊥ xy.
Suy ra .
Xét ∆AOC và ∆DOB có:
OC = OB (giả thiết)
(chứng minh trên)
OD = OA (giả thiết)
Do đó ∆AOC = ∆DOB (c.g.c)
Suy ra DB = AC (hai cạnh tương ứng)
Gọi E là giao điểm của AC và BD.
Ta có .
Suy ra ∆AEB vuông tại E nên AC ⊥ BD.
b) Vì AC = BD (chứng minh trên) mà M, N lần lượt là trung điểm của AC, BD
Nên BN = DN = AM = CM.
Xét ∆ONB và ∆OMC có:
BN = CM (chứng minh trên)
(vì ∆AOC = ∆DOB)
OC = OB (giả thiết)
Do đó ∆ONB = ∆OMC (c.g.c)
Suy ra OM = ON (hai cạnh tương ứng).
c) Từ câu b: ∆ONB = ∆OMC suy ra (hai góc tương ứng)
Ta có .
Gọi P là trung điểm của MN.
Xét ∆NOP và ∆MOP có:
OM = ON (chứng minh trên)
MP = NP (vì P là trung điểm của MN)
Cạnh OP chung
Do đó ∆NOP = ∆MOP (c.c.c)
Suy ra (hai cạnh tương ứng)
Do đó .
Vậy các góc của tam giác MON là .
Bài 4. (1,0 điểm)
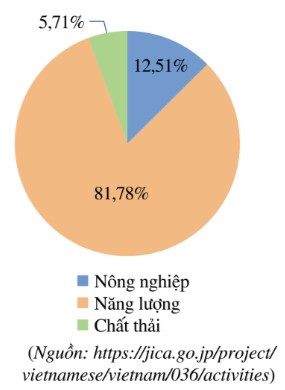
a) Lượng khí nhà kính được tạo ra ở lĩnh vực Năng lượng của Việt Nam vào năm 2020 là:
466 . 81,78% = 381,0948 (triệu tấn khí carbonic tương đương)
Lượng khí nhà kính được tạo ra ở lĩnh vực chất thải của Việt Nam vào năm 2020 là:
466 . 5,71% = 26,6086 (triệu tấn khí carbonic tương đương).
Vậy lượng khí nhà kính được tạo ra của Việt Nam vào năm 2020 ở lĩnh vực Năng lượng là 381,0948 triệu tấn khí carbonic tương đương và Chất thải là 26,6086 triệu tấn khí carbonic tương đương.
b) Nêu đúng hai trong những biện pháp sau:
- Trồng nhiều cây xanh, không phá rừng bừa bãi.
- Sử dụng hiệu quả và tiết kiệm năng lượng; sử dụng và phát triển những nguồn năng lượng sạch.
- Khuyến khích người dân sử dụng phương tiện công cộng.
- Tái sử dụng và tái chế những vật dụng có khả năng tái sử dụng và tái chế.
- Tuyên truyền, nâng cao ý thức và giáo dục người dân về hậu quả của khí thải, hiệu ứng nhà kính.
Đề thi giữa kì 2 Toán lớp 7 Cánh diều có đáp án - Đề 3
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Cánh diều
Năm học ..................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 3)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Câu 1. Thảo ghi chiều cao (cm) của các bạn học sinh tổ 1 lớp 7A được ghi lại trong bảng sau:
|
130 |
145 |
− 150 |
141 |
155 |
151 |
Số liệu không hợp lí là
A. 155;
B. 141;
C. − 150;
D. 130.
Câu 2. Cho biểu đồ dưới đây
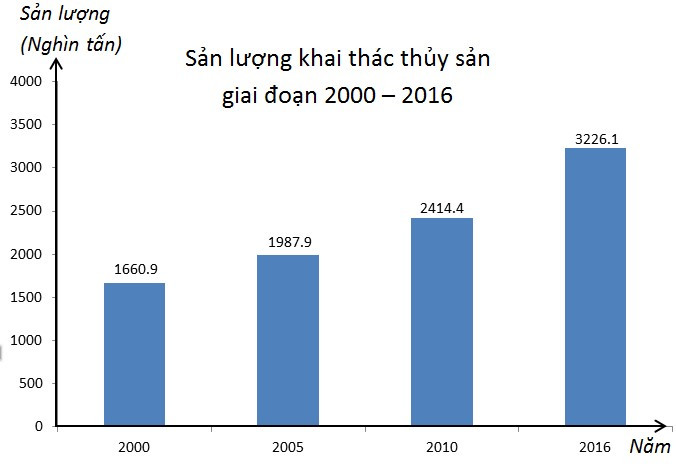
Tiêu chí thống kê là
A. Giai đoạn 2000 – 2006;
B. Các năm: 2000; 2005; 2010; 2016;
C. Thủy sản;
D. Sản lượng khai thác thủy sản (nghìn tấn).
Câu 3. Biểu đồ đoạn thẳng trong hình dưới đây biểu diễn điểm bài ôn luyện môn Khoa học của bạn Khanh từ tuần 1 đến tuần 5.
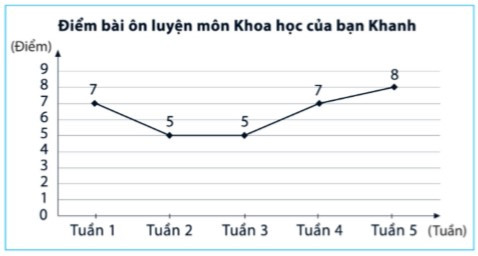
Hãy cho biết điểm 7 của bạn Khanh đạt vào tuần nào?
A. Tuần 1 và tuần 2;
B. Tuần 1 và tuần 4;
C. Tuần 2 và tuần 4;
D. Tuần 2 và tuần 5.
Câu 4. Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn loại thực phẩm yêu thích trong 5 loại: Bánh rán, Nước ép, Bánh, Trà, Cà phê của học sinh khối 7 ở trường THCS Thanh Đa. Mỗi học sinh chỉ được chọn một loại thực phẩm khi được hỏi ý kiến như hình bên dưới.
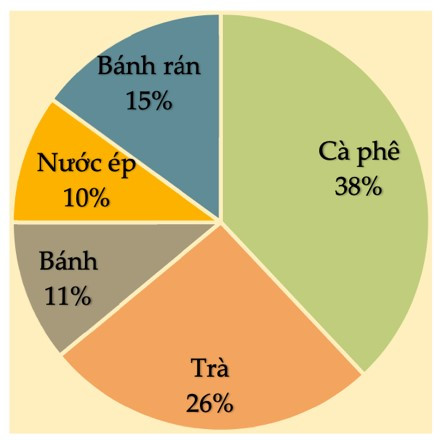
Hỏi tổng số học sinh chọn món Trà và Bánh rán chiếm bao nhiêu phần trăm?
A. 41%;
B. 36%;
C. 64%;
D. 37%.
Câu 5. Khi tung một đồng xu cân đối một lần và quan sát mặt xuất hiện của nó. Số kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là
A. 1;
B. 2;
C. 3;
D. 4.
Câu 6. Xác suất của biến cố trong trò chơi có 10 kết quả có thể xảy ra là . Số kết quả thuận lợi của biến cố đó là
A. 5;
B. 2;
C. 4;
D. 6.
Câu 7. Cho ∆ABC vuông tại A. Khi đó
A. ;
B. ;
C. ;
D. .
Câu 8. Cho tam giác ABC. Bất đẳng thức nào dưới đây sai?
A. AB + AC > BC;
B. BC – AB < AC;
C. BC + AB > AC;
D. BC – AC > AB.
Câu 9. Cho ∆ABC = ∆MNP. Khẳng định nào dưới đây sai?
A.;
B. ;
C. AB = MP;
D. BC = NP.
Câu 10. Cho tam giác ABC và DEH trong hình dưới đây.
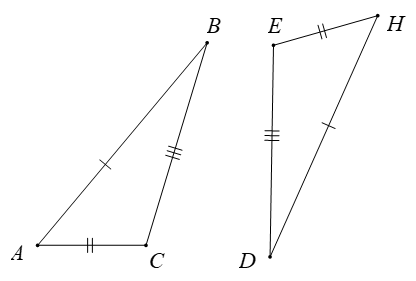
Khẳng định đúng là
A. ∆ABC = ∆DEH;
B. ∆ABC = ∆HDE;
C. ∆ABC = ∆EDH;
D. ∆ABC = ∆HED.
Câu 11. Cho tam giác ABC và tam giác NPM có BC = PM; . Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh?
A. AC = NM;
B. AB = NP;
C. ;
D. .
Câu 12. Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H và K. So sánh BH và CK.
A. BH < CK;
B. BH = 2CK;
C. BH > CK;
D. BH = CK.
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm) Xét tính hợp lí của các dữ liệu trong mỗi bảng thống kê sau:
a)
|
Lớp |
Sĩ số |
Số học sinh tham gia ngoại khóa |
|
7A1 |
39 |
42 |
|
7A2 |
42 |
10 |
|
7A3 |
45 |
15 |
|
7A4 |
43 |
26 |
|
Tổng |
169 |
60 |
b)
|
Kết quả kiểm tra thường xuyên môn Toán đợt 1 |
Tỉ lệ phần trăm |
|
Từ 8 điểm trở lên |
45% |
|
Từ 6,5 điểm đến 7,9 điểm |
110% |
|
Từ 5,0 điểm đến 6,4 điểm |
35% |
|
Từ 3,5 điểm đến 4,9 điểm |
10% |
|
Dưới 3,5 điểm |
200% |
Bài 2. (1,0 điểm) Một hộp có 48 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; …; 48. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chính phương”.
Bài 3. (3,0 điểm) Cho ∆ABC có AB < AC. Kẻ tia phân giác AD của (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC.
a) Chứng minh ∆BDF = ∆EDC.
b) Chứng minh ba điểm F, D, E thẳng hàng.
c) Chứng minh AD ⊥ FC.
Bài 4. (1,0 điểm) Năm 2020, Việt Nam xuất khẩu (ước đạt) 6,5 triệu tấn gạo, thu được 3,07 tỉ đô la Mỹ. Biểu đồ hình quạt tròn ở bên dưới biểu diễn khối lượng xuất khẩu của mỗi loại gạo trong tổng số gạo xuất khẩu (tính theo tỉ số phần trăm).
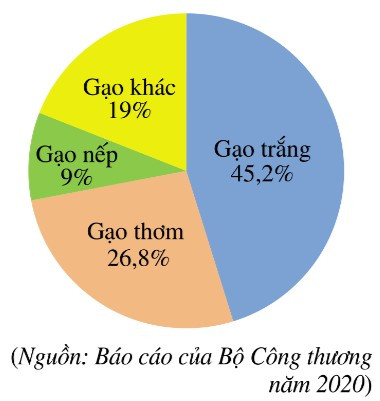
Dựa vào thông tin thu thập từ biểu đồ trên để trả lời các câu hỏi sau:
a)Tính số lượng gạo trắng và số lượng gạo nếp được xuất khẩu năm 2020?
b) Số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm là bao nhiêu?
ĐÁP ÁN ĐỀ SỐ 2
I. Bảng đáp án trắc nghiệm
|
1. C |
2. D |
3. B |
4. A |
5. B |
6. C |
|
7. A |
8. D |
9. C |
10. B |
11. A |
12. D |
II. Hướng dẫn giải trắc nghiệm
Câu 4.
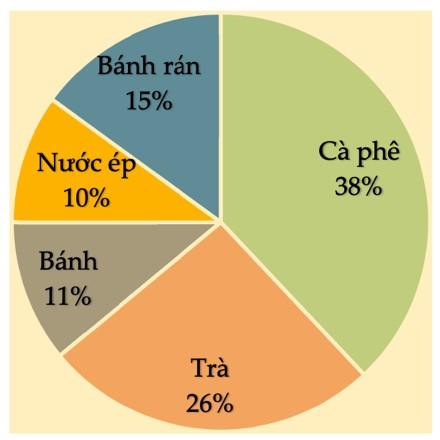
Tổng tỉ số phần trăm số học sinh chọn món Trà và Bánh rán là:
26% + 15% = 41%.
Câu 6.
Gọi số kết quả thuận lợi của biến cố đó là k.
Khi đó xác suất của biến cố đó là .
Theo bài ta có: =
Suy ra k = 4.
Vậy số kết quả thuận lợi của biến cố là 4.
Câu 9.
Vì ∆ABC = ∆MNP nên:
; ; (các góc tương ứng bằng nhau)
AB = MN; BC = NP; AC = MP (các cạnh tương ứng bằng nhau)
Vậy AB = MP là khẳng định sai.
Câu 11.
Vì tam giác ABC và tam giác NPM có BC = PM; .
Nên để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh cần thêm điều kiện AC = NM. (Do là góc xen giữa hai cạnh BC và AC; là góc xen giữa hai cạnh PM và NM).
Câu 12.
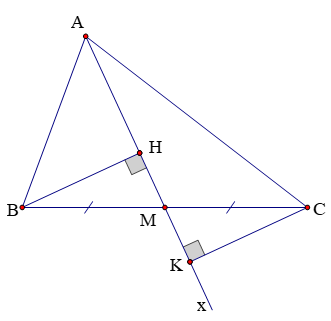
Xét hai tam giác vuông BHM và CKM có
BM = CM (vì M là trung điểm của BC)
(hai góc đối đỉnh)
Suy ra ∆BHM và ∆CKM (cạnh huyền – góc nhọn).
Do đó BH = CK (hai cạnh tương ứng).
I. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm)
a) Bảng thống kê này chưa hợp lí:
• Số học sinh lớp 7A1 tham gia ngoại khoá (42 học sinh) vượt quá sĩ số của lớp (39 học sinh);
• Tổng số học sinh tham gia ngoại khoá của các lớp là:
42 + 10 + 15 + 26 = 93 (học sinh).
Tổng số học sinh tham gia ngoại khoá của các lớp (93 học sinh) lớn hơn số học sinh ở phần tổng (60 học sinh) nên bảng thống kê này chưa hợp lí.
b) Bảng thống kê này chưa hợp lí vì tỉ lệ phần trăm kết quả kiểm tra thường xuyên không thể vượt quá 100% (cột tỉ lệ phần trăm kiểm tra thường xuyên môn Toán đợt 1 dưới 3,5 điểm là 200% vượt quá 100%) và tổng các loại phải đúng bằng 100%.
Bài 2. (1,0 điểm)
Tập hợp các kết quả có thể xảy ra là: {1; 2; 3; … ; 47; 48}. Có 48 kết quả.
Trong các số trên, số chính phương là: 1; 4; 9; 16; 25; 36.
Do đó có 6 kết quả thuận lợi.
Khi đó, xác suất của biến cố đã cho là: .
Vậy xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chính phương” bằng .
Bài 3. (3,0 điểm)
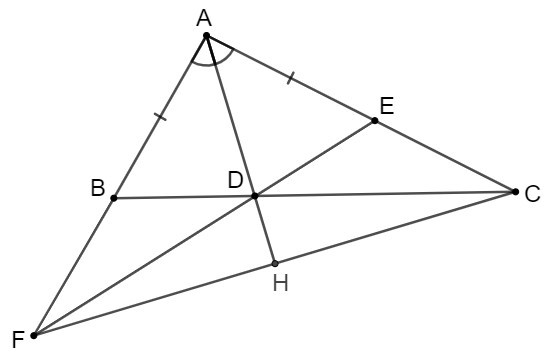
Xét ∆BDF và ∆EDC có:
AE = AB (giả thiết)
(vì AD là tia phân giác của )
Cạnh AD chung
Do đó ∆BDF = ∆EDC (c.g.c).
Suy ra BD = ED (hai cạnh tương ứng); (hai cạnh tương ứng).
Mặt khác ; nên .
Ta có AF = AC, AB = AE suy ra BF = EC.
Xét ∆BDF và ∆EDC có:
BF = EC (chứng minh trên)
(chứng minh trên)
BD = ED (chứng minh trên)
Do đó ∆BDF = ∆EDC (c.g.c).
b) Từ câu a: ∆BDF = ∆EDC suy ra (hai góc tương ứng).
Mà nên .
Do đó ba điểm F, D, E thẳng hàng.
c) Gọi H là giao điểm của AD và CF.
Xét ∆AHF và ∆AHC có:
AF = AC (giả thiết)
(vì AD là tia phân giác của )
Cạnh AH chung
Do đó ∆AHF = ∆AHC (c.g.c).
Suy ra (hai cạnh tương ứng).
Mà suy ra .
Vậy AH ⊥ FC hay AD ⊥ FC.
Bài 4. (1,0 điểm)
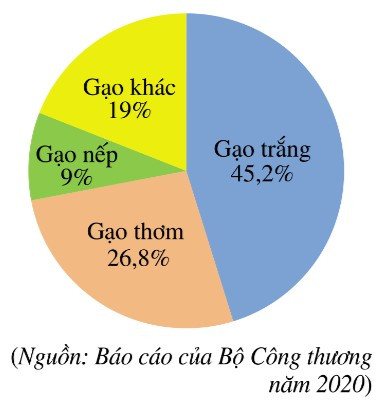
a) Số lượng gạo trắng được xuất khẩu năm 2020 là:
6,5 . 45,2% = 2,938 (triệu tấn).
Số lượng gạo nếp được xuất khẩu năm 2020 là:
6,5 . 9% = 0,585 (triệu tấn).
Vậy số lượng gạo trắng và số lượng gạo nếp được xuất khẩu năm 2020 lần lượt là 2,938 triệu tấn và 0,585 triệu tấn.
b) Số lượng gạo thơm được xuất khẩu là:
6,5 . 26,8% = 1,742 (triệu tấn).
Tỉ số phần trăm số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm là:
2,938 – 1,742 = 1,196 (triệu tấn).
Đề thi giữa kì 2 Toán lớp 7 Cánh diều có đáp án - Đề 4
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Cánh diều
Năm học ..................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 4)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.
Câu 1. Ngọc tìm hiểu về các loài hoa yêu thích của các bạn trong lớp 7A và thu được kết quả như bảng dưới đây:
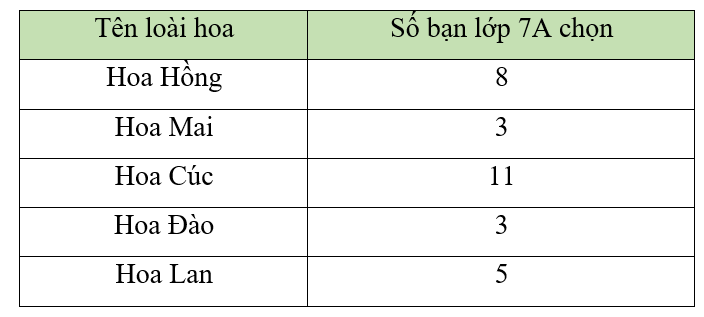
Dữ liệu nào dưới đây là dữ liệu không phải là số?
A. Hoa Hồng;
B. 8;
C. 16;
D. 3.
Câu 2. Cho biểu đồ cột (hình vẽ) biểu diễn mật độ số dân số một số vùng nước ta năm 2006.
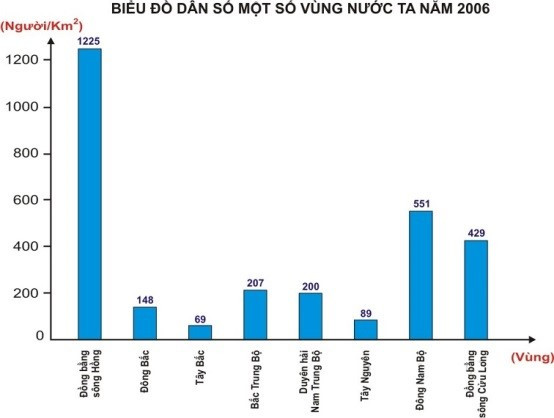
Số khu vực có mật độ dân số không vượt quá 200 người/km2 là
A. 2;
B. 3;
C. 4;
D. 5.
Câu 3. Biểu đồ đoạn thẳng trong hình bên dưới biểu diễn số học sinh đạt điểm giỏi trong bốn lần kiểm tra môn Toán của lớp 7A: lần 1, lần 2, lần 3, lần 4.
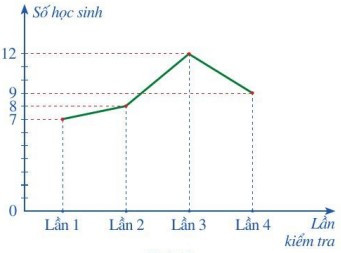
Số học sinh đạt điểm giỏi ở lần kiểm tra thứ hai là
A. 7;
B. 8;
C. 9;
D. 12;
Câu 4. Cho biểu đồ như hình vẽ.
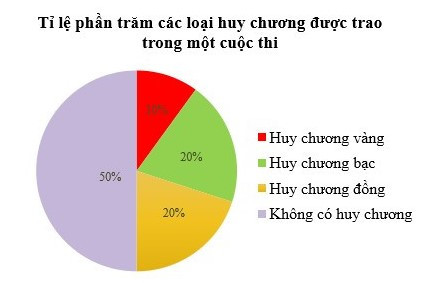
Hãy cho biết đối tượng nào chiếm tỉ lệ phần trăm cao nhất?
A. Huy chương vàng;
B. Huy chương bạc;
C. Huy chương đồng;
D. Không có huy chương.
Câu 5. Trong một trò chơi, Xuân được chọn làm người may mắn để rút thăm trúng thưởng. Gồm 4 loại thăm: hai hộp bút màu, hai bức tranh, một đôi giày và một cái bàn. Xuân được rút thăm một lần. Tập hợp các kết quả có thể xảy ra đối với lá thăm Xuân rút được là
A. {hai hộp bút màu; hai bức tranh; một đôi giày; một cái bàn};
B. {hai hộp bút màu; hai bức tranh; một đôi giày};
C. {hai hộp bút màu; hai bức tranh};
D. {Không trúng thưởng}.
Câu 6. Trong trò chơi gieo 2 đồng xu, các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là 4. Nếu k là số kết quả thuận lợi cho biến cố thì xác suất của biến cố đó bằng
A. 2k;
B. 4k;
D. .
Câu 7. Tổng ba góc của một tam giác bằng
A. 90°;
B. 100°;
C. 120°;
D. 180°.
Câu 8. Cho tam giác ABC có AB – AC = 2 (cm). So sánh đúng là
A. ;
B. ;
C. ;
D. .
Câu 9. Hai tam giác bằng nhau là hai tam giác có:
(I) Ba cạnh tương ứng bằng nhau.
(II) Ba góc tương ứng bằng nhau.
Chọn khẳng định đúng:
A. Chỉ có (I) đúng;
B. Chỉ có (II) đúng;
C. Cả (I) và (II) đều đúng;
D. Cả (I) và (II) đều sai.
Hai tam giác trên bằng nhau theo trường hợp
A. cạnh – cạnh – cạnh;
B. cạnh – góc – cạnh;
C. góc – cạnh – góc;
D. Cả A, B, C đều sai.
Câu 11. Cho hình vẽ dưới đây, biết CE = DE và .
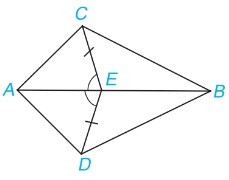
Khẳng định sai là
A. ∆AEC = ∆AED ;
B. AC = AD;
C. AE là tia phân giác của góc CAD;
D. .
Câu 12. Cho ∆DEF có . Tia phân giác của góc D cắt EF tại I. Khẳng định nào sau đây là đúng?
A. ;
B. ∆DIE = ∆FDI;
C. IE = IF, DE = DF;
D. .
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Cho các dãy dữ liệu sau. Phân loại mỗi dãy dữ liệu dưới thuộc loại nào (dựa trên các tiêu chí định tính và định lượng)?
a) Thủ đô một số quốc gia châu Á: Hà Nội; Tokyo, Viêng Chăn, Bangkok.
b) Số học sinh các lớp của khối 6 trong trường THCS Nguyễn Trãi như sau: 39; 40; 38; 39; 38.
Bài 2. (1,0 điểm) Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được kết quả như hình vẽ sau:

a) Hãy lập bảng thống kê và cho biết có bao nhiêu người tham gia cuộc khảo sát?
b) Tính tỉ lệ phần trăm của loại nước nhiều người ưa chuộng nhất .
Bài 3. (1,0 điểm) Một bài thi trắc nghiệm có 16 câu hỏi được đánh số từ 1 đến 16. Chọn ngẫu nhiên một câu hỏi trong bài thi. Xét hai biến cố sau:
A: “Số thứ tự của câu hỏi được chọn là số có một chữ số”;
B: “Số thứ tự của câu hỏi được chọn là số có hai chữ số”.
Tính xác suất của hai biến cố A và B.
Bài 4. (1,0 điểm) Cho tam giác ABC có = 90°, = 30°. Điểm D thuộc cạnh AC sao cho = 20°. So sánh các độ dài các cạnh của ∆BDC.
Bài 5. (2,0 điểm) Cho hình thang ABCD (AB // CD) có AB = BC và ; .
a) Chứng minh ∆ABM = ∆CBM.
b) Tính số đo .
Bài 6. (1,0 điểm) Biểu đồ bên dưới thể hiện các loại hình giải trí trong thời gian rảnh rỗi của 300 học sinh khối 7 của trường A.
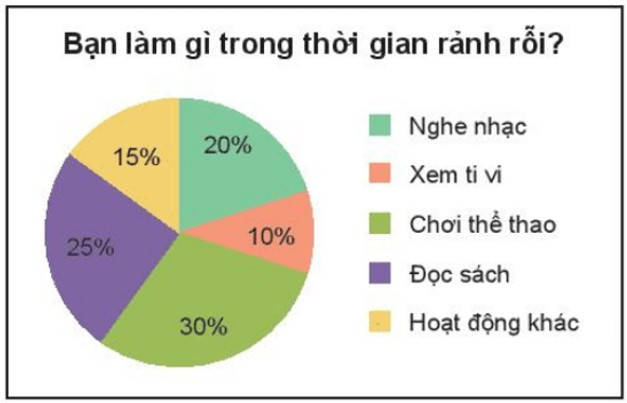
Em hãy cho biết có khoảng bao nhiêu bạn thích đọc sách hoặc chơi thể thao trong thời gian rảnh rỗi?
Đề thi giữa kì 2 Toán lớp 7 Cánh diều có đáp án - Đề 5
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 2 - Cánh diều
Năm học ..................
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 5)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Điều tra số con của 4 hộ gia đình trong ngõ thu được kết quả như bảng dưới đây

Dữ liệu nào dưới đây là dữ liệu số?
A. Nguyễn Văn Anh;
B. Hoàng Trọng Việt;
C. Lê Văn Nam;
D. 3.
Câu 2. Cho biểu đồ (hình vẽ) thể hiện giá trị so sánh của xuất khẩu và nhập khẩu nước ta giai đoạn 1990 – 2005.
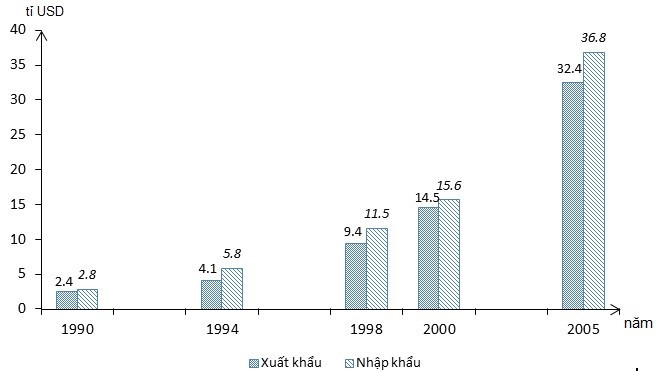
Giá trị nhập khẩu năm 2005 là
A. 32,4 tỉ USD;
B. 36,8 tỉ USD;
C. 69,2 tỉ USD;
D. 4,4 tỉ USD.
Câu 3. Biểu đồ đoạn thẳng trong hình bên biểu diễn lượng mưa trung bình 6 tháng đầu năm của một địa phương năm 2020.
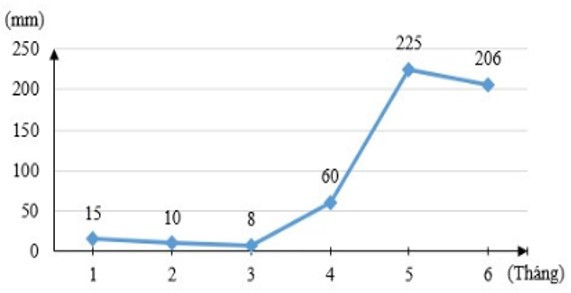
Hãy cho biết lượng mưa tăng trong những khoảng thời gian nào?
A. Tháng 1 – tháng 2;
B. Tháng 3 – tháng 4;
C. Tháng 5 – tháng 6;
D. Cả B và C đều đúng.
Câu 4. Cho biểu đồ hình quạt tròn (hình vẽ)
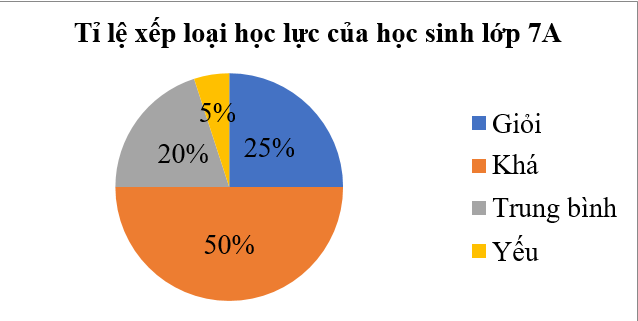
Tính số học sinh của lớp 7A biết số học sinh yếu của lớp 7A là 2 em.
A. 35;
B. 40;
C. 45;
D. 50.
Câu 5. Một hộp có 28 viên bi đồng kích cỡ, mỗi viên bi được ghi một trong các số 1; 2; 3; …; 27; 28. Hai viên bi khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một viên bi trong hộp. Xét biến cố “Số xuất hiện trên viên bi được rút ra là số không lớn hơn 14”. Nêu những kết quả thuận lợi cho biến cố trên.
A. 1; 2; 3; … ; 12; 13;
B. 1; 2; 3; ... ; 13; 14;
C. 14; 15; 16; ... ; 27; 28;
D. 15; 16; ... ; 27; 28.
Câu 6. Gieo ngẫu nhiên xúc xắc 1 lần. Tính xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn”.
A. 3;
B. ;
C. 2;
D. .
Câu 7. Cho hình vẽ, biết rằng BE, CF lần lượt là tia phân giác của , và .
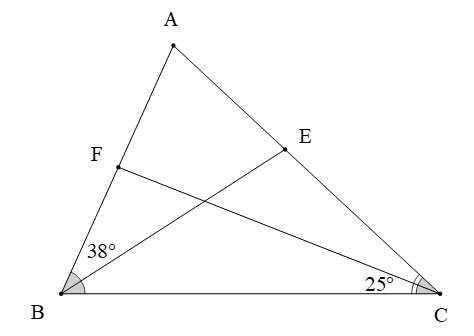
Số đo của là
A. 52°;
B. 54°;
C. 56°;
D. 58°.
Câu 8. Cho tam giác MPQ có MP = 3 cm và PQ = 6 cm. So sánh góc Q và góc P đúng là
A. ;
B. ;
C. ;
D. Không đủ điều kiện để so sánh.
Câu 9. Cho ∆ABC = ∆MNP có AB = 3 cm; AC = 4 cm; PN = 5 cm. Chu vi ∆MNP là
A. 12 cm;
B. 7 cm;
C. 9 cm;
D. 6 cm.
Câu 10. Cho hình vẽ dưới đây, biết AB = CD; AD = BC. Góc có số đo bằng góc ABC là
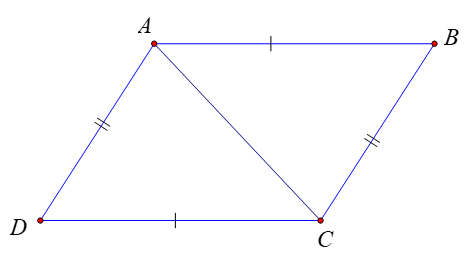
A. ;
B. ;
C. ;
D. .
Câu 11. Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC và BA = BE. Số đo góc BED là
A. 30°;
B. 60°;
C. 90°;
D. 50°.
Câu 12. Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm I tùy ý, qua I vẽ đường thẳng vuông góc với OI cắt Ox ở E và cắt Oy ở F. Trong các khẳng định sau, khẳng định nào đúng?
A. ∆OEI = ∆OIF;
B. IE = OF;
C. OE = OI;
D. .
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Thống kê về các loại lồng đèn mà các bạn học sinh lớp 7B làm được để trao tặng cho các trẻ em khuyết tật nhân dịp Tết Trung thu được cho bởi bảng thống kê sau:
|
STT |
Loại lồng đèn |
Số lượng |
|
1 |
Con cá |
8 |
|
2 |
Thiên nga |
6 |
|
3 |
Con thỏ |
3 |
|
4 |
Ngôi sao |
7 |
|
5 |
Đèn xếp |
15 |
a) Hãy phân loại các dữ liệu trong bảng thống kê trên dựa vào tiêu chí định tính và định lượng.
b) Tính tổng số lồng đèn các loại mà các bạn lớp 7B đã làm được.
Bài 2. (2,0 điểm) Quan sát biểu đồ dưới đây và trả lời các câu hỏi.
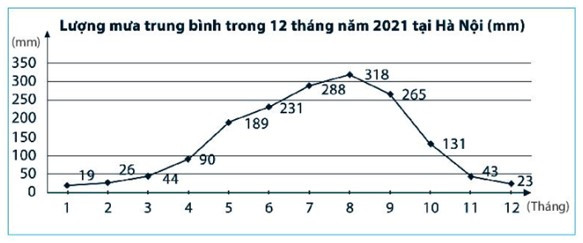
a) Biểu đổ biểu diễn các thông tin về vấn đề gì? Đơn vị thời gian là gì?
c) Tháng nào có lượng mưa trung bình cao nhất? Tháng nào có lượng mưa trung bình thấp nhất?
Bài 3. (1,0 điểm) Viết ngẫu nhiên một số tự nhiên nhỏ hơn 2021. Tính xác suất của biến cố “Số tự nhiên được viết là số chia hết cho 7”.
Bài 4. (2,0 điểm) Cho tam giác ABC vuông tại B (AB < AC) có AM là tia phân giác góc A (M ∈ BC). Trên cạnh AC lấy điểm N sao cho AB = AN.
a) Chứng minh ∆ABM = ∆ANM.
b) Chứng minh .
Bài 5. (1,0 điểm) Ba vị trí của khu vực A, B, C trong một trường học được mô tả như hình vẽ dưới đây.
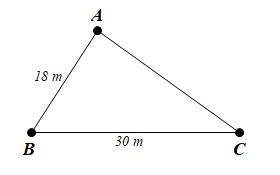
Nếu đặt ở khu vực A một thiết bị phát wifi thì cần có bán kính hoạt động là bao nhiêu để cả hai khu vực B và C đều nhận được tín hiệu?