Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 6 Bài 22: Hình có tâm đối xứng sách Kết nối tri thức. Tài liệu gồm 15 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:

Trắc nghiệm Toán lớp 6 Bài 22: Hình có tâm đối xứng

Phần 1. Trắc nghiệm Hình có tâm đối xứng

I. Nhận biết

Câu 1. Trong các hình: Hình bình hành, hình chữ nhật, hình vuông, hình lục giác đều, hình thoi thì có bao nhiêu hình không có tâm đối xứng?

A. 0

B. 1

C. 2

D. 3

Lời giải

Tất cả các hình trên đều có tâm đối xứng.

Do đó không có hình nào không có tâm đối xứng.

Đáp án: A

Câu 2. Khẳng định nào dưới đây là sai về tam giác đều?

A. Tam giác đều có ba trục đối xứng

B. Tam giác đều có tâm đối xứng là giao điểm của ba trục đối xứng

C. Tam giác đều không có tâm đối xứng

D. Tam giác đều có ba cạnh bằng nhau

Lời giải

Tam giác đều có ba cạnh bằng nhau nên D đúng.

Tam giác đều có ba trục đối xứng nối đỉnh với trung điểm cạnh đối diện. Do đó A đúng.

Tam giác đều không có tâm đối xứng nên C đúng, B sai.

Đáp án: B

Câu 3. Trong các biển báo giao thông sau đây, biển nào có tâm đối xứng?

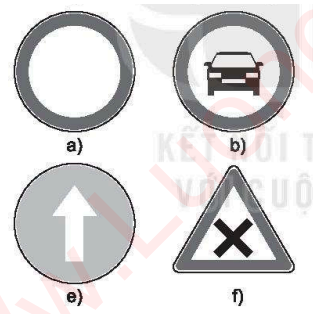
A. Hình a)

B. Hình b)

C. Hình e)

D. Hình f)

Lời giải Biên báo có tâm đối xứng là biển báo ở hình a).

Đáp án: A

Câu 4. Trong các số dưới đây, số nào có tâm đối xứng

A. 4

B. 0

C. 6

D. 9

Lời giải Số có tâm đối xứng là số 0.

Đáp án: B

Câu 5. Hình nào dưới đây không có tâm đối xứng

A. Lục giác đều

B. Tam giác đều

C. Hình bình hành

D. Hình thoi

Lời giải Tam giác đều là hình không có tâm đối xứng.

Đáp án: B

Câu 6. Cho hình vẽ sau:

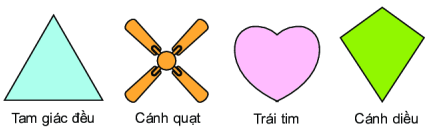
Có bao nhiêu hình có tâm đối xứng?

A. 1

B. 2

C. 3

D. 4

Lời giải Hình cánh quạt là hình có tâm đối xứng.

Đáp án: A

Câu 7. Tâm đối xứng của hình tròn là:

A. Tâm của đường tròn

B. Một điểm bất kì nằm bên trong đường tròn

C. Một điểm bất kì nằm trên đường tròn

D. Một điểm bất kì nằm bên ngoài đường tròn.

Lời giải Tâm đối xứng của hình tròn là tâm của đường tròn.

Đáp án: A

Câu 8. Hình nào dưới đây không có tâm đối xứng

A. Hình bình hành

B. Hình thoi

C. Hình chữ nhật

D. Hình thang cân

Lời giải Hình thang cân là hình không có tâm đối xứng.

Đáp án: D

Câu 9. Trong các hình dưới đây, điểm O là tâm đối xứng của hình nào?

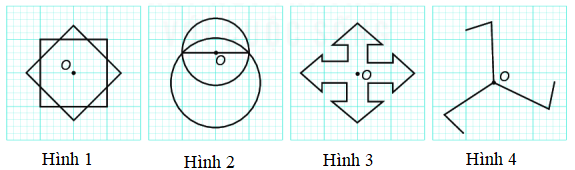
A. Hình 1 và Hình 2

B. Hình 1 và Hình 3

C. Hình 1 và Hình 4

D. Hình 1, Hình 3 và Hình 4

Lời giải Trong các hình đã cho, hình nhận tâm O là tâm đối xứng là các hình: Hình 1 và Hình 3.

Đáp án: B

Câu 10. Phát biểu nào dưới đây là đúng?

A. Hình thoi có tâm đối xứng nhưng không có trục đối xứng.

B. Hình thang cân có trục đối xứng, nhưng không có tâm đối xứng.

C. Hình bình hành vừa có tâm đối xứng, vừa có trục đối xứng.

D. Hình chữ nhật có trục đối xứng nhưng không có tâm đối xứng.

Lời giải

- Hình thoi có hai trục đối xứng là hai đường chéo, và tâm đối xứng là giao điểm của hai đường chéo nên A sai.

- Hình thang cân có trục đối xứng, nhưng không có tâm đối xứng nên B đúng.

- Hình bình hành có tâm đối xứng nhưng không có trục đối xứng nên C sai.

- Hình chữ nhật vừa có trục đối xứng, vừa có tâm đối xứng nên D sai.

Đáp án: B

II. Thông hiểu

Câu 1. Em hãy vẽ thêm vào hình vẽ dưới đây để được hình có điểm O là tâm đối xứng:

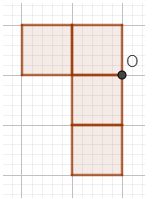
A.

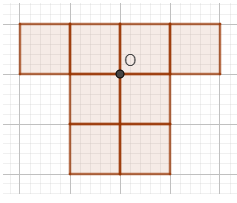
B.

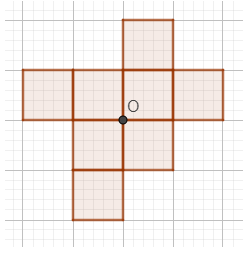
C.

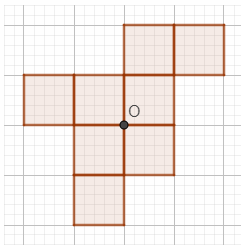
D.

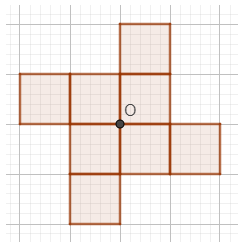
Lời giải

Hình sau khi vẽ thêm nhận O làm tâm đối xứng là:

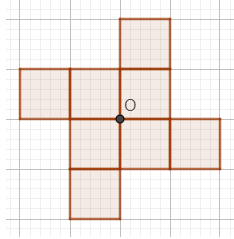
Đáp án: D

Câu 2. Các phát biểu sau đúng hay sai? Có bao nhiêu phát biểu sai?

a) Tam giác đều ABC là hình đối xứng tâm.

b) Hình thang cân là hình có tâm đối xứng và giao điểm của hai đường chéo là tâm đối xứng.

c) Hình thoi ABCD có tâm đối xứng là điểm O (O là giao điểm của hai đường chéo AC và BD).

A. 0

B. 1

C. 2

D. 3

Lời giải

Tam giác đều ABC là hình không có tâm đối xứng. Do đó phát biểu a) sai.

Hình thang cân là hình không có tâm đối xứng nên phát biểu b sai.

Hình thoi là hình có tâm đối xứng là giao điểm của hai đường chéo nên phát biểu c) đúng.

Đáp án: C

Câu 3. Trong Hình 39, các hình từ hình a) đến e), hình nào có tâm đối xứng?

A. Hình a), Hình e)

B. Hình a), Hình c)

C. Hình a), Hình b), Hình c)

D. Hình a), Hình c), Hình e)

Lời giải

Trong các hình trên, hình có tâm đối xứng là:

Hình a) là hình có tâm đối xứng và tâm đối xứng là trung điểm O của AB.

Hình c) là hình có tâm đối xứng và tâm đối xứng là giao điểm của hai đường chéo MP và QN.

Hình e) là hình có tâm đối xứng như hình vẽ bên dưới:

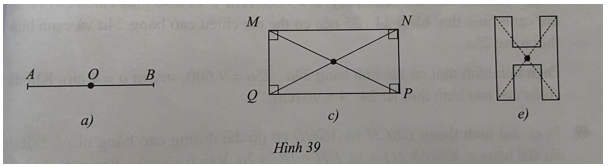
Đáp án: D

Câu 4. Trong Hình 40, các hình từ a) đến e), họa tiết viên gạch hoa nào không có tâm đối xứng?

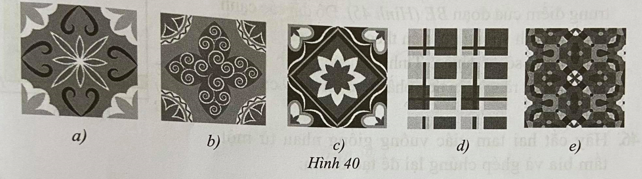
A. Cả 4 hình

B. Hình 40a) và Hình 40b)

C. Hình 40c) và Hình 40e)

D. Hình 40b) và Hình 40d)

Lời giải Hình không có tâm đối xứng là: Hình 40b) và Hình 40d).

Đáp án: D

Câu 5. Cho đoạn thẳng MN dài 18cm. Biết O là tâm đối xứng của MN. Tính ON

A. 9cm

B. 8cm

C. 18cm

D. 6cm

Lời giải Do O là tâm đối xứng của đoạn thẳng MN nên độ dài đoạn OM bằng độ dài ON bằng độ dài MN chia 2 bằng: 18:2 = 9 cm.

Đáp án: A

Phần 2. Lý thuyết Hình có tâm đối xứng

1. Hình có tâm đối xứng trong thực tế

Mỗi hình có mổ điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được “trùng khít” với chính nó ở vị trí ban đầu (trước khi quay).

Những hình như thế được gọi là “hình có tâm đối xứng” và điểm O được gọi là “tâm đối xứng” của hình.

Ví dụ 1. Đoạn thẳng là một hình có tâm đối xứng. Tâm đối xứng của nó là điểm nào?

Lời giải

Cho đoạn thẳng AB có trung điểm là điểm O

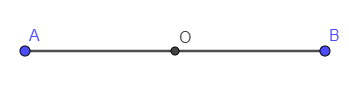
Khi quay đoạn thẳng AB xung quanh điểm O đúng nửa vòng ta thư được hình sau:

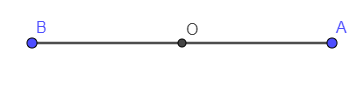
Hình thu được là một hình trùng khít với hình ban đầu. 

Do đó đoạn thẳng là một hình có tâm đối xứng và tâm đối xứng của nó là điểm O.

Ví dụ 2. Trong những hình nào dưới đây hình nào có tâm đối xứng? Hãy dự đoán tâm đối xứng và kiểm tra bằng cách quay nửa vòng.

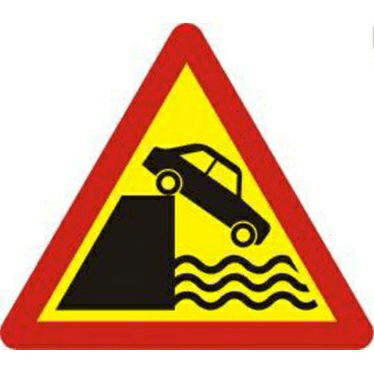
             Hình a                                 Hình b                                    Hình c

Lời giải

Hình có tâm đối xứng là hình a

Tâm đối xứng của hình là tâm O của đường tròn.

Khi quay biển báo một nửa vòng quanh tâm O ta được:

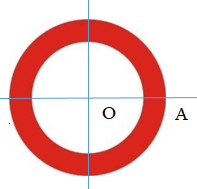
Hình này trùng khít với hình ban đầu.

Do đó hình này có tâm đối xứng và tâm đối xứng là tâm O của đường tròn.

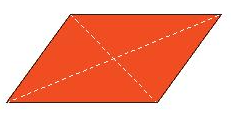
2. Tâm đối xứng của một số hình phẳng

Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.

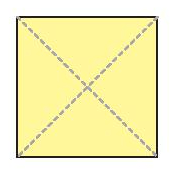
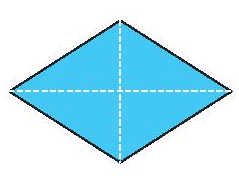
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.

Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài 21: Hình có trục đối xứng

Trắc nghiệm Bài 22: Hình có tâm đối xứng

Trắc nghiệm Bài 23: Mở rộng phân số. Phân số bằng nhau

Trắc nghiệm Bài 24: So sánh phân số. Hỗn số dương

Trắc nghiệm Bài 25: Phép cộng và phép trừ phân số