Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 6 Bài 12: Bội chung. Bội chung nhỏ nhất sách Kết nối tri thức. Tài liệu gồm 23 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:

Trắc nghiệm Toán lớp 6 Bài 12: Bội chung. Bội chung nhỏ nhất

Phần 1. Trắc nghiệm Bội chung. Bội chung nhỏ nhất

I. Nhận biết

Câu 1. Cho biết BC(4, 6) = {0; 12; 24; 36; 48; …}. Hãy cho biết BCNN(4, 6).

A. BCNN(4,6) = 0.

B. BCNN(4, 6) = 12.

C. BCNN(4, 6) = 24.

D. BCNN(4, 6) = 36.

Lời giải

Trong tập hợp BC(4, 6) ta thấy bội chung nhỏ nhất khác 0 là 12.

Nên BCNN(4, 6) = 12.

Đáp án: B

Câu 2. Nếu $20⋮a$  và $20⋮b$  thì 20 là ………………….. của a và b.

A. ước chung.

B. bội chung.

C. ước chung lớn nhất.

D. bội chung nhỏ nhất.

Lời giải

Nếu $20⋮a$  và $20⋮b$ thì 20 là bội chung của a và b.

Đáp án: B

Câu 3. Nếu 30 là số tự nhiên nhỏ nhất mà 30  a và 30  b thì 30 là …………….. của a và b.

A. ước chung.

B. bội chung.

C. ước chung lớn nhất.

D. bội chung nhỏ nhất.

Lời giải Nếu 30 là số tự nhiên nhỏ nhất mà 30  a và 30  b thì 30 là bội chung nhỏ nhất của a và b.

Đáp án: D

Câu 4. Cho m = 3.5² và n = 5².7. Tìm ƯCLN(m, n):

A. 5;

B. 25;

C. 75;

D. 105.

Lời giải

Ta có: m = 3.5² và n = 5².7.

Tích các thừa số chung với số mũ nhỏ nhất là: 5². 

ƯCLN(m, n) = 5² = 25.

Đáp án: B

Câu 5. Cho m = 2².3.5 và n = 2.3².5. Tìm BCNN(m, n):

A. 30;

B. 60;

C. 90;

D. 180.

Lời giải

Ta có m = 2².3.5 và n = 2.3².5

Tích các thừa số chung và riêng với số mũ lớn nhất là: 2².3².5 = 180.

BCNN(m, n) = 180.

Đáp án: D

Câu 6. Một số tự nhiên a khác 0 nhỏ nhất thỏa mãn $a⋮12$ và $a⋮36$ . Khi đó a là:

A. ƯC(12, 36).

B. BC(12, 36).

C. ƯCLN(12, 36).

D. BCNN(12, 36).

Lời giải

Vì $a⋮12$ và $a⋮36$ nên a là bội chung của 12 và 36.

Mà a là số tự nhiên khác 0 nhỏ nhất nên a chính là BCNN(12, 36).

Đáp án: D

Câu 7. Sắp xếp các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

1 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

2 – Chọn ra các thừa số nguyên tố chung và riêng.

3 – Phân tích mỗi số ra thừa số nguyên tố.

A. 1 – 2 – 3.

B. 2 – 3 – 1.

C. 3 – 1 – 2.

D. 3 – 2 – 1.

Lời giải

Các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

3 – Phân tích mỗi số ra thừa số nguyên tố.

2 – Chọn ra các thừa số nguyên tố chung và riêng.

1 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

Đáp án: D

Câu 8. Bội chung của hai hay nhiều số là gì: 

A. là một tập hợp.

B. là ước của tất cả các số đó.

C. là bội của tất cả các số đó.

D. A, B và C đều đúng.

Lời giải Bội chung của hai hay nhiều số là bội của tất cả các số đó.

Đáp án: C

Câu 9. Nếu x  a, x b thì:

A. x ∈ BC(a, b).

B. x là BCNN(a, b).

C. x ∈ ƯC(a,b).

D. x là ƯCLN(a, b).

Lời giải

Nếu $x⋮a, x⋮b$ thì x BC(a, b).

Đáp án: B

Câu 10. Mọi số tự nhiên a và b khác 0 ta có:

A. BCNN(a, b, 1) = a.

B. BCNN(a, b, 1) = b.

C. BCNN(a, b, 1) = 1.

D. BCNN(a, b, 1) = BCNN(a, b).

Lời giải

Mọi số tự nhiên đều là bội của 1. Do đó với  mọi số tự nhiên a và b (khác 0), ta có:

BCNN(a, b, 1) = BCNN(a, b).

Đáp án: D

II. Thông hiểu

Câu 1. Biết BCNN(84, 70) = 2^x.3^y.5^z.7^t. Tính tích x.y.z.t:

A. 0;                               B. 2;                      C. 5;                      D. 3.

Lời giải

Ta có: 84 = 2².3.7;  70 = 2.5.7.

Tích các thừa số chung và riêng với số mũ lớn nhất là: 2².3.5.7.

Do đó BCNN(84, 70) = 2².3.5.7.

Khi đó x = 2, y = 1, z = 1, t = 1.

Vậy x.y.z.t = 2.1.1.1 = 2.

Đáp án: B

Câu 2. Hai số có BCNN là 2³.3.5³ và ƯCLN là 2².5. Biết một trong hai số bằng 2².3.5, tìm số còn lại.

A. 2².1.5³;             B. 2.1.5³;                        C. 2².1.5²;             D. 2.1.5

Lời giải

Ta có tích hai số đúng bằng tích của BCNN và ƯCLN.

Nên số còn lại là: (2³.3.5³.2².5) : (2².3.5) = (2⁵.3.5⁴):(2².3.5) 

= (2⁵:2³).(3:3).(5⁴:5) = 2².1.5³.

Vậy số cần tìm là: 2².1.5³.

Đáp án: A

Câu 3. Phát biểu nào dưới đây là đúng?

A. $\frac{15}{17}$ là phân số tối giản.

B. BCNN(25; 15) = .

C.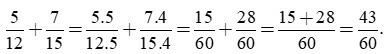  

D. Cả A, B và C đều đúng.

Lời giải

+) Ta có ƯCLN(15,17) = 1 nên $\frac{15}{17}$  là phân số tối giản. Do đó A đúng.

+) Ta có 25 = 5²; 15 = 3.5 

Tích các thừa số chung và riêng với số mũ lớn nhất là: 3.5².

BCNN(15, 25) = 3.5² = 3.25 = 75. Do đó B sai.

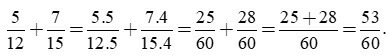+)  Do đó C sai.

Suy ra D sai.

Đáp án: A

Câu 4. Tìm BCNN(56, 24, 21).

A. 8;

B. 168;

C. 21;

D. 24.

Lời giải

Ta có 56 = 2³.7; 24 = 2³.3; 21 = 3.7.

Tích các thừa số chung và riêng với số mũ lớn nhất là: 2³.3.7.

BCNN(56, 24, 21) = 2³.3.7 = 8.3.7 = 168.

Đáp án: B

Câu 5. Bạn Nam thực hiện phép tính $\frac{5}{20}+\frac{9}{26}$ như sau:

Bước 1: Rút gọn phân số : 

Bước 2: 4 = 2², 26 = 2.13. Suy ra BCNN(4, 26) = 2.13 = 26 suy mẫu chung là 26.

Bước 3: Khi đó: 26:4 = 6, 26:26 = 1. Ta có:  

Hỏi bạn Nam sai từ bước nào?

A. Bước 1;                      

B. Bước 2;                      

C. Bước 3;                      

D. Không sai bước nào.

Lời giải

Bạn Nam sai từ bước 2(bước tìm mẫu số chung). 

Sửa lại

Bước 1: Rút gọn phân số :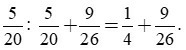  

Bước 2: 4 = 2², 26 = 2.13. Suy ra BCNN(4, 26) = 2².13 = 52 suy mẫu chung là 52.

Bước 3: Khi đó: 52:4 = 13, 52:26 = 2. Ta có:

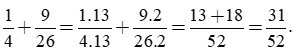
Đáp án: B

Câu 6. Cho hai số tự nhiên 15 và 25. Tập hợp BC(15, 25) là:

A. BC(15, 25) = 75.

B. BC(15, 25) = 0; 75; 150; 225; …

C. BC(15, 25) = {0; 75; 150; 225; …}.

D. BC(15, 25) = {75}.

Lời giải

Ta có: 15 = 3.5; 25 = 5².

Tích các thừa số chung và riêng với số mũ lớn nhất là: 3.5².

BCNN(15, 25) = 3.5² = 3.25 = 75.

BC(15, 25) = B(75) = {0; 75; 150; 225; …}.

Đáp án: C

Câu 7. Tìm bội chung nhỏ hơn 200 của 3, 4 và 7.

A. 84.

B. 0; 84.

C. 0; 84; 168.

D. 84; 168.

Lời giải

Ta có: 3 = 3; 4 = 2²;  7 = 7.

Khi đó BCNN(3, 4, 7) = 3.2².7 = 84.

Suy ra BC(3, 4, 7) = B(84) = {0; 84; 168; 252; …}.

Bội chung nhỏ hơn 200 của 3, 4 và 7 là 0; 84; 168.

Đáp án: C

Câu 8. Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng $a⋮28$  và $a⋮32$ 

A. a = 32.

B. a = 28.

C. a = 224.

D. a = 0.

Lời giải

Vì $a⋮28$  và $a⋮32$  nên a là BC(28, 32).

Mà a là nhỏ nhất nên a là BCNN(28, 32).

Ta có: 28 = 2².7; 32 = 2⁵.

Tích các thừa số chung và riêng với số mũ lớn nhất là: 2⁵.7.

BCNN(28, 32) = 2⁵.7 = 32.7 = 224.

Vậy a = 224.

Đáp án: C

Câu 9. Quy đồng mẫu các phân số sau: $\frac{5}{14} và \frac{4}{21}$ 

A. Hai phân số sau khi quy đồng: $\frac{10}{21} và \frac{4}{21}$ 

B. Hai phân số sau khi quy đồng: $\frac{15}{21} và \frac{4}{21}$ 

C. Hai phân số sau khi quy đồng: $\frac{15}{42} và \frac{8}{42}$ 

D. Hai phân số sau khi quy đồng: $\frac{10}{42} và \frac{8}{42}$ 

Lời giải

Ta có 14 = 7.2; 21 = 7.3.

BCNN(14; 21) = 7.2.3 = 42.

Khi đó 42:14 = 3; 42:21 = 2, ta được: 

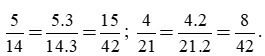
Vậy hai phân số sau khi quy đồng: $\frac{15}{42} và \frac{8}{42}$ 

Đáp án: C

Câu 10. Thực hiện phép tính:$\frac{7}{11}+\frac{5}{7}$ 

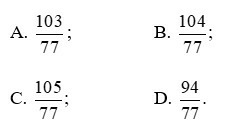
Lời giải

Mẫu chung là BCNN(7, 11) = 77. Khi đó: 

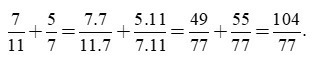
Đáp án: B

III. Vận dụng

Câu 1. Tìm các số tự nhiên a và b (a < b), biết ƯCLN(a, b) = 15 và BCNN(a, b) = 180. Hỏi có bao nhiêu cặp số a và b như thế? 

A. 0;

B. 1;

C. 2;

D. 3

Lời giải

Đặt a = 15m, b = 15 n với , m < n và ƯCLN(m, n) = 1.

Ta có: ab = ƯCLN(a, b).BCNN(a, b) = 15.180 = 2 700.

Do đó (15m).(15n) = 2700

Hay 15.15.m.n = 2 700

225.m.n = 2 700

m.n = 12 = 1.12 = 3.4 = 2.6.

Vì m, n là các số tự nhiên khác 0 thỏa mãn m < n và nguyên tố cùng nhau nên:

+) m = 1, n = 12 suy ra a = 15, b = 180.

+) m = 3, n = 4 suy ra a = 45; n = 60.

Vậy có 2 cặp (a, b).

Đáp án: C

Câu 2. Trong một buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia. Thầy tổng phụ trách cho xếp thành hàng 5, hàng 6 và hàng 8 thì đều thừa một người. Hỏi có chính xác bao nhiêu người dự buổi tập đồng diễn thể dục.

A. 480;

B. 481;

C. 360;

D. 361.

Lời giải

Gọi số người tham gia buổi tập đồng diễn thể dục là x (, 400 < x < 500).

Do số người tham gia xếp thàng hàng 5, hàng 6 và hàng 8 đều thừa một người nên ta có:

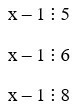
nên x – 1 BC(5, 6, 8).

Ta có 5 = 5, 6 = 2.3, 8 = 2³.

Khi đó: BCNN(5, 6, 8) = 2³.3.5 = 8.3.5 = 120.

Suy ra BC(5, 6, 8) = B(120) = .

Do đó x – 1 .

Hay x .

Mà 400 < x < 500 nên x = 481. 

Đáp án: B

Câu 3. Học sinh lớp 6A khi xếp thành hàng 2, hàng 3, hàng 7 đều vừa đủ hàng. Hỏi số học sinh lớp 6A là bao nhiêu, biết rằng số học sinh nhỏ hơn 45?

A. 42;

B. 45;

C.21;

D. 35.

Lời giải

Số học sinh lớp 6A khi xếp thành hàng 2, hàng 3, hàng 7 đều vừa đủ nên số học sinh là bội chung của 2, 3 và 7. 

Ta có: 2 = 2, 3 = 3, 7 = 7. 

BCNN(2, 3, 7) = 2.3.7 = 42.

BC(2, 3, 7) = B(42) = {0; 42; 84; 126; …}.

Mà số học sinh nhỏ hơn 45 nên số học sinh của 6A là 42 học sinh.

Đáp án: A

Phần 2. Lý thuyết Bội chung. Bội chung nhỏ nhất

1. Bội chung và bội chung nhỏ nhất

Bội chung của hai hay nhiều số là bội của tất cả các số đã cho.

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Kí hiệu:

BC(a, b) là tập hợp các bội chung của a và b.

BCNN(a, b) là bội chung nhỏ nhất của a và b.

Ví dụ 1. Tìm bội chung và bội chung nhỏ nhất của 30 và 45

Lời giải 

Ta có B(30) = {0; 30; 60; 90; 120; 150; 180; 210; 240; 270; …}

B(45) = {0; 45; 90; 135; 180; 225; 270; …}

BC(30, 45) = {0; 90; 180; 270; …}.

BCNN(30, 45) = 90.

Nhận xét: Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất đó. 

Nếu a 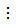b thì BCNN(a, b) = a.

Mọi số tự nhiên đều là bội của 1. Do đó với mọi số tự nhiên a và b (khác 0), ta có: 

BCNN(a, 1) = a; BCNN(a, b, 1) = BCNN(a, b).

Ví dụ 2. Tìm bội chung nhỏ nhất của các số sau:

a) 12 và 36;

b) 124 và 1.

Lời giải

a) Vì 36 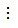12 nên BCNN(12, 36) = 36;

b) Vì 124 là bội của 1 nên BCNN(1; 124) = 124.

2. Cách tìm bội chung nhỏ nhất

Các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

Bước 1. Phân tích mỗi số ra thừa số nguyên tố;

Bước 2. Chọn ra các thừa số nguyên tố chung và riêng;

Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

Ví dụ 3. Tìm bội chung nhỏ nhất của 21 và 14.

Lời giải

Ta có 21 = 3.7; 14 = 2.7.

Khi đó BCNN(21, 14) = 2.3.7 = 42.

Tìm bội chung từ bội chung nhỏ nhất

Để tìm bội chung của các số đã cho ta có thể làm như sau:

Bước 1. Tìm BCNN của các số đã cho.

Bước 2. Tìm các bội của BCNN đó.

Ví dụ 4. Tìm BC(12, 24, 30) 

Lời giải

Ta có: 12 = 2².3; 24 = 2³.3; 30 = 2.3.5.

BCNN(12, 24, 30) = 2³.3.5 = 120.

BC(12, 24, 30) = B(120) = {0; 120; 240; 360; 480; …}.

3. Quy đồng mẫu các phân số

Vận dụng BCNN để tìm mẫu chung của hai phân số:

Để quy đồng mẫu số hai phân số 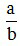  và 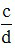 , ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là BCNN của hai mẫu.

Ví dụ 5. Quy đồng mẫu số các phân số sau:

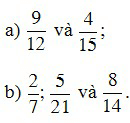
Lời giải

a) Ta có 12 = 2².3; 15 = 3.5.

BCNN(12, 15) = 2².3.5 = 60.

Ta có: 60:12 = 5; 60:15 = 4. Khi đó:

 

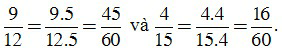
b) Ta có: 7 = 7, 21 = 3. 7, 14 = 2.7.

BCNN(7, 21, 14) = 2.3.7 = 42.

Ta có: 42:7 = 6, 42:21 = 2, 42:14 = 3. Khi đó:

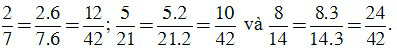
Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài 11: Ước chung. Ước chung lớn nhất

Trắc nghiệm Bài 12: Bội chung. Bội chung nhỏ nhất

Trắc nghiệm Bài 13: Tập hợp các số nguyên

Trắc nghiệm Bài 14: Phép cộng và phép trừ số nguyên

Trắc nghiệm Bài 15: Quy tắc dấu ngoặc