Với giải bài tập Toán lớp 6 Bài 2: Biểu đồ cột kép chi tiết bám sát nội dung sgk Toán 6 Tập 2 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6 . Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 2: Biểu đồ cột kép
Trả lời câu hỏi giữa bài
Giải Toán 6 trang 10 Tập 2 Cánh diều
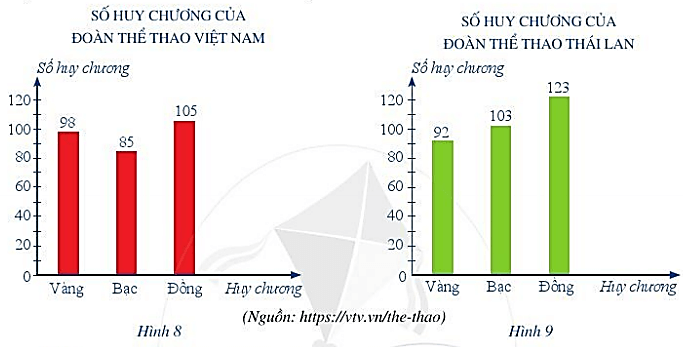
Làm thế nào để biểu diễn được đồng thời từng loại huy chương của cả hai đoàn Việt Nam và Thái Lan trên cùng một biểu đồ cột?
Lời giải:
Để biểu diễn được đồng thời từng loại huy chương của cả hai đoàn Việt Nam và Thái Lan trên cùng một biểu đồ cột ta sẽ sử dụng biểu đồ cột kép – sẽ được giới thiệu trong bài học này.
Quan sát Biểu đồ cột kép ở Hình 10 ta thấy:
- Đối tượng thống kê là các loại huy chương: Vàng, Bạc, Đồng. Các đối tượng này lân lượt được biểu diễn ở trục nằm ngang.
- Tiêu chí thống kê là số huy chương mỗi loại của mỗi nước.
- Ứng với mỗi đối tượng thống kê có một số liệu thống kê theo tiêu chí, lần lượt được biểu diễn ở trục thẳng đứng.
- Trong biểu diễn thống kê của Đoàn Thể thao Việt Nam, các cột đều được tô màu đỏ và được quy định bằng hình chữ nhật màu đỏ ở phía trên của biểu đồ.
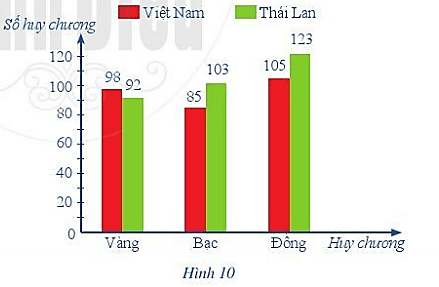
Trong biểu diễn thống kê của Đoàn Thể thao Thái Lan, các cột đều được tô màu xanh và được quy định bằng hình chữ nhật màu xanh ở phía trên của biểu đồ.
Giải Toán 6 trang 12 Tập 2 Cánh diều
Biết rằng mỗi học sinh chỉ nêu một môn thể thao yêu thích nhất.
a) Môn thể thao nào có nhiều học sinh thích chơi nhất?
b) Tính tổng số học sinh của lớp 6C.
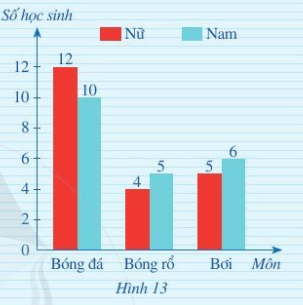
Lời giải:
a) Quan sát biểu đồ, ta thấy cột bóng đá màu đỏ và cột bóng đá màu xanh là cột cao nhất tương ứng với 12 học sinh nữ và 10 học sinh nam yêu thích. Do đó môn thể thao có nhiều học sinh thích chơi nhất là bóng đá.
b) Vì mỗi học sinh chỉ yêu thích một môn thể thao nên số học sinh của lớp 6C chính là tổng số học sinh nam và nữ yêu thích các môn thể thao và bằng:
12 + 10 + 4 + 5 + 5 + 6 = 42 (học sinh)
Vậy lớp 6C có 42 học sinh.
Bài tập
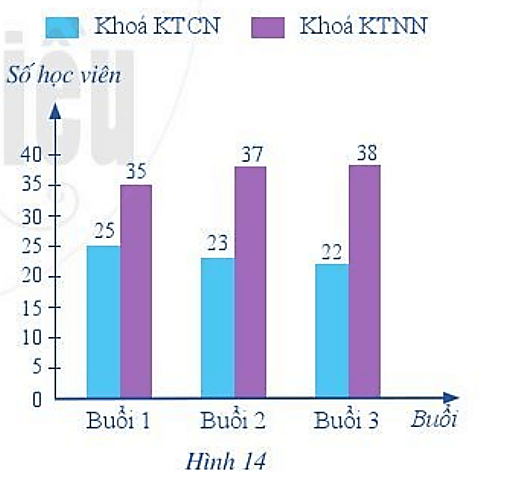
a) Trong ba buổi đầu tiên. số học viên dùng nước giải khát ở mỗi buổi là bao nhiêu?
b) Dựa vào biểu đồ ở Hình 14, so sánh số lượt học viên dùng nước giải khát của khóa bồi dưỡng về KTCN với khóa bồi dưỡng về KTNN trong mỗi buổi.
c) Để tránh lãng phí trong những buổi học tiếp theo, em hãy chọn phương án phù hợp nhất đối với việc chuẩn bị nước giải khát cho học viên của cả hai khoá bồi đưỡng (biết mỗi lượt học viên dùng 1 cốc nước giải khát):
1. 40 cốc nước giải khát; 2. 45 cốc nước giải khát;
3. 60 cốc nước giải khát; 4. 80 cốc nước giải khát.
Lời giải:
a) Số lượt học viên dùng nước ở buổi 1 là: 25 + 35 = 60 (lượt học viên).
Số lượt học viên dùng nước ở buổi 2 là: 23 + 37 = 60 (lượt học viên).
Số lượt học viên dùng nước ở buổi 3 là: 22 + 38 = 60 (lượt học viên).
Vậy tổng số lượt học viên dùng nước ở mỗi buổi là 60 lượt học viên.
b) Dựa vào biểu đồ Hình 14, ta thấy số lượt học viên dùng nước giải khát của khoa KTNN nhiều hơn so với số lượt học viên dùng nước giải khát của khoa KTCN.
c) Vì tổng số lượt học viên dùng nước ở mỗi buổi là 60 lượt học viên nên để tránh lãng phí trong những buổi học tiếp theo ta nên chọn phương án 3.
Giải Toán 6 trang 13 Tập 2 Cánh diều
b) Biết rằng sau hai ngày nói trên, cửa hàng lãi được 700 000 đồng và cửa hàng 2 đã lãi được 400 000 đồng. Nhận định “Bán được càng nhiều áo thì càng lãi nhiều” có hợp lí không?
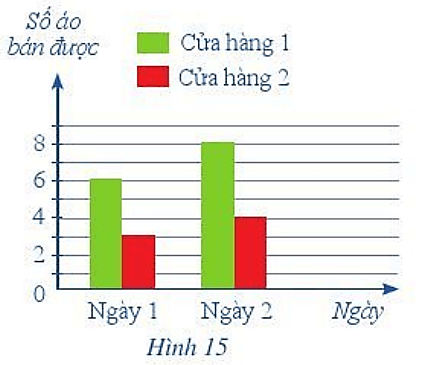
Lời giải:
a) Trong hai ngày cửa hàng 1 đã bán được: 6 + 8 = 14 (cái áo).
Trong hai ngày cửa hàng 2 đã bán được: 3 + 4 = 7 (cái áo).
Vậy trong hai ngày cửa hàng 1 đã bán được 14 cái áo, cửa hàng 2 bán được 7 cái áo.
b) Nhận định “Bán được càng nhiều áo thì càng lãi nhiều” là hợp lí vì cửa hàng 1 bán được 14 cái áo lãi 700 000, còn cửa hàng 2 bán được 7 cái áo lãi 400 000 (700 000 > 400 000).
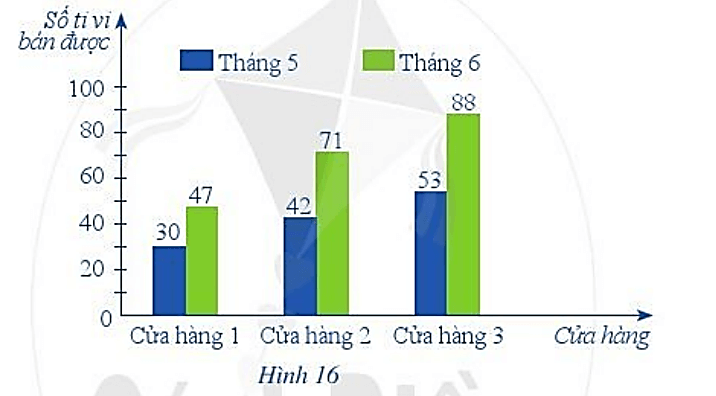
a) So sánh số lượng ti vi bán được của mỗi cửa hàng trong tháng 5 và trong tháng 6.
b) Cửa hàng 3 bán được nhiều ti vi nhất trong cả tháng 5 và tháng 6. Em có thể đưa ra một lí do phù hợp nhất để giải thích cho kết quả này được không? Em đồng ý với những nhận xét nào sau đây:
1. Cửa hàng 3 bán ti vi với giá rẻ nhất;
2. Cửa hàng 3 chăm sóc khách hàng tốt nhất;
3. Cửa hàng 3 có nhiều loại ti vi cho người mua hàng lựa chọn;
4. Cửa hàng 3 ở vị trí thuận lợi cho việc đi lại mua bán của người mua hàng?
c) Số lượng ti vi mà cả ba cửa hàng bán được trong tháng 6 nhiều hơn số lượng ti vi mà cả ba cửa hàng bán được trong tháng 5 là bao nhiêu chiếc? Em có biết giải bóng đá World Cup 2018 diễn ra vào tháng nào không? Sự kiện đó có liên quan đến việc mua bán ti vi trong tháng 6 hay không?
d) Nếu 20 năm sau (tính từ năm 2018) em có một cửa hàng bán ti vi thì em chọn thời gian nào để có thể bán được nhiều ti vi nhất trong năm?
Lời giải:
a) So sánh số lượng ti vi bán được trong tháng 5 và tháng 6 ở mỗi cửa hàng:
Ở cả 3 cửa hàng, số ti vi bán được của tháng 6 luôn nhiều hơn tháng 5. Cụ thể:
Cửa hàng 1: Số ti vi bán được ở tháng 6 nhiều hơn tháng 5 là: 47 – 30 = 17 (ti vi)
Cửa hàng 2: Số ti vi bán được ở tháng 6 nhiều hơn tháng 5 là: 71 – 42 = 29 (ti vi)
Cửa hàng 3: Số ti vi bán được ở tháng 6 nhiều hơn tháng 5 là: 88 – 53 = 35 (ti vi)
b) Mỗi học sinh sẽ có những lựa chọn khác nhau (vì lý do nào cũng hợp lý).
Ý kiến cả nhân của em là đồng ý với nhận xét: (2), (4)
c) Số lượng ti vi mà cả ba cửa hàng bán được trong tháng 6 nhiều hơn số lượng ti vi mà cả ba cửa hàng bán được trong tháng 5 là: (47 + 71 + 88) - (30 + 42 + 53) = 81 (ti vi)
Giải bóng đá World Cup 2018 diễn ra vào tháng 6, tháng 7 hàng năm. Sự kiện đó có liên quan đến việc mua bán ti vi vì vào thời điểm đó, nhu cầu xem cao, sức mua tăng, vì thế lượng ti vi bán được nhiều.
d) Nếu 20 năm sau (tính từ năm 2018) em có một cửa hàng bán ti vi thì em chọn tháng 6 để có thể bán được nhiều ti vi nhất trong năm.
Xem thêm các bài giải SGK Toán lớp 6 Cánh diều hay, chi tiết khác:
Giải SGK Toán 6 Bài 1: Thu thập, tổ chức, biểu diễn, phân tích và xử lí dữ liệu
Giải SGK Toán 6 Bài 3: Mô hình xác suất trong một số trò chơi và thí nghiệm đơn giản
Giải SGK Toán 6 Bài 4: Xác suất thực nghiệm trong một trò chơi và thí nghiệm đơn giản
Giải SGK Toán 6 Bài ôn tập cuối chương 4
Lý thuyết Biểu đồ cột kép
Biểu đồ cột kép dùng để biểu diễn được đồng thời từng số liệu của hai dãy dữ liệu cùng loại, ghép hai biểu đồ cột thành một Biểu đồ cột kép
+ Các đối tượng thống kê biểu diễn ở trục nằm ngang.
+ Ứng với mỗi đối tượng thống kê có một cặp số liệu thống kê theo tiêu chí, lần lượt biểu diễn ở trục thẳng đứng.
+ Mỗi đối tượng được biểu diễn dưới dạng cột hình chữ nhật và quy định màu khác nhau ở phía trên biểu đồ
Ví dụ: Biểu đồ cột kép dưới đây biểu diễn xếp loại học lực (Giỏi, Khá, Trung bình, Yếu) của khối lớp 6 tại của một trường có hai lớp 6A và 6B.
a) Học lực nào của lớp 6A và lớp 6B có nhiều học sinh nhất?
b) Tổng số học sinh của lớp 6A và 6B là bao nhiêu?
c) Giáo viên chủ nhiệm của lớp 6A khẳng định rằng lớp 6A có tỉ số phần trăm học sinh Giỏi và Khá so với cả lớp cao hơn lớp 6B có đúng không?
Hướng dẫn giải
a) Quan sát biểu đồ cột màu xanh biểu diễn cho số học sinh của lớp 6A ta thấy số học sinh có học lực Giỏi nhiều nhất.
Quan sát biểu đồ cột màu cam biểu diễn cho số học sinh của lớp 6B ta thấy số học sinh có học lực Khá nhiều nhất.
b) Tổng số học sinh của lớp 6A là: 20 + 11 + 7 + 2 = 40 (học sinh)
Tổng số học sinh của lớp 6B là: 7 + 25 + 8 + 4 = 44 (học sinh).
c) Số học sinh Giỏi và Khá của lớp 6A là: 20 + 11 = 31 (học sinh)
Số học sinh Giỏi và Khá của lớp 6B là: 7 + 25 = 32 (học sinh)
Tỉ số phần trăm của học sinh Giỏi và Khá so với cả lớp 6A là:
Tỉ số phần trăm của học sinh Giỏi và Khá so với cả lớp 6B là:
Vì 77,5 > 72,7272… nên tỉ số phần trăm cú học sinh Giỏi và Khá so với cả lớp của lớp 6A cao hơn lớp 6B.
Vậy khẳng định của cô giáo chủ nhiệm lớp 6A là đúng.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
