Với giải bài tập Toán lớp 6 Bài 14: Phép cộng và phép trừ số nguyên chi tiết bám sát nội dung sgk Toán 6 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán lớp 6 Bài 14: Phép cộng và phép trừ số nguyên
Video giải Toán 6 Bài 14: Phép cộng và phép trừ số nguyên - Kết nối tri thức
Trả lời câu hỏi giữa bài
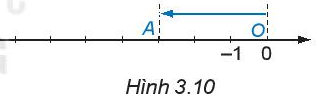
Lời giải:
Vì từ gốc O trên trục số, di chuyển sang trái 3 đơn vị đến điểm A ta được điểm A biểu diễn số -3.
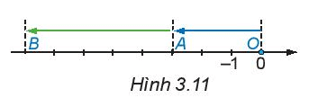
Lời giải:
Vì từ điểm A (điểm biểu diễn số -3) di chuyển sang trái 5 đơn vị ta được điểm B. Do đó điểm B biểu diễn số -8.
Mà B chính là điểm biểu diễn kết quả của phép cộng (-3) + (-5) nên (-3) + (-5) = -8
Luyện tập 1 trang 62 Toán lớp 6 Tập 1: Thực hiện các phép cộng sau:
(- 12) + (- 48)
(- 236) + (- 1 025)
Lời giải:
Ta có: (- 12) + (- 48) = - (12 + 48) = -60;
Ta có: (- 236) + (- 1 025) = - (236 + 1 025) = - 1 261.
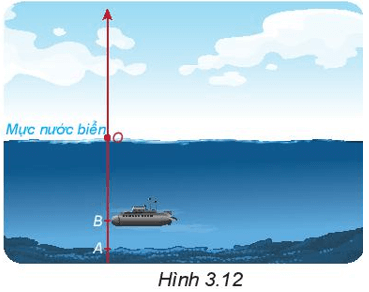
Một chiếc tàu ngầm cần lặn (coi là theo phương thẳng đứng) xuống điểm A dưới đáy biển. Khi tàu đến điểm B ở độ cao – 135 m, máy đo báo rằng tàu còn cách A một khoảng 45 m. Hỏi điểm A nằm ở độ cao bao nhiêu mét?
Lời giải:
Tàu ở độ cao -135m và còn phải lặn thêm 45m, tức là đi -45m nữa mới đến A. Do đó A nằm ở độ cao:
(-135) + ( -45) = - (135 + 45) = - 180 (mét)
Vậy điểm A nằm ở độ cao - 180 mét.
Câu hỏi trang 63 Toán lớp 6 Tập 1: Tìm số đối của 4; -5; 9; -11.
Lời giải:
+) Hai điểm 4 và -4 có cùng khoảng cách đến gốc O nên số đối của 4 là -4.
+) Hai điểm 5 và -5 có cùng khoảng cách đến gốc O nên số đối của -5 là 5.
+) Hai điểm 9 và -9 có cùng khoảng cách đến gốc O nên số đối của 9 là -9.
+) Hai điểm 11 và -11 có cùng khoảng cách đến gốc O nên số đối của -11 là 11.
Lời giải:
Số đối của 5 là -5; số đối của -2 là 2.
Biểu diễn trên trục số:
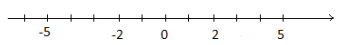
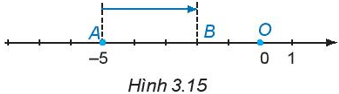
Lời giải:
Từ điểm A biểu diễn số - 5 trên trục số di chuyển sang phải 3 đơn vị đến điểm B ta được điểm B biểu diễn số -2. Điểm B biểu diễn của phép cộng (-5) + 3.
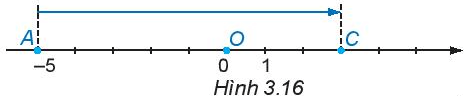
Lời giải:
Từ điểm A biểu diễn số - 5 trên trục số di chuyển sang phải 8 đơn vị đến điểm C ta được điểm B biểu diễn số 3. Điểm C biểu diễn của phép cộng (-5) + 8.
Luyện tập 3 trang 64 Toán lớp 6 Tập 1: Thực hiện các phép tính:
a) 203 + (- 195);
b) (- 137) + 86.
Lời giải:
a) 203 + (- 195) = 203 - 195 = 8 (do 203 > 195);
b) (- 137) + 86 = - (137 - 86) = - 51 (do 137 > 86).
Vận dụng 2 trang 64 Toán lớp 6 Tập 1: Sử dụng phép cộng hai số nguyên khác dấu để giải bài toán sau:
Một máy thăm dò đáy biển ngày hôm trước hoạt động ở độ cao – 946 m (so với mực nước biển). Ngày hôm sau người ta cho máy nổi lên 55 m so với hôm trước. Hỏi ngày hôm sau máy thăm dò đáy biển hoạt động ở độ cao nào?
Lời giải:
Vì máy nổi lên 55 m so với hôm trước nghĩa là máy di chuyển theo chiều dương
Ngày hôm sau, máy thăm dò hoạt động ở độ cao:
(- 946) + 55 = - (946 -55) = -891 (m)
Vậy ngày hôm sau, máy thăm dò hoạt động ở độ cao -891 m.
Tranh luận trang 64 Toán lớp 6 Tập 1:

Lời giải:
Ta có thể đưa ra 1 số ví dụ sau:
Ví dụ 1: Hai số nguyên khác dấu là: 5 và -7.
Khi đó tổng của chúng là 5 + (-7) = -(7 -5) = -2 (do 7 > 2) là số âm
Ví dụ 2: Hai số nguyên khác dấu là: 9 và -4.
Khi đó tổng của chúng là 9 + (-4) = 9 - 4 = 5 (do 9 > 4) là số dương
Ví dụ 3: Hai số nguyên khác dấu là: 4 và -4.
Khi đó tổng của chúng là 4 + (-4) = 0 (đây là tổng của hai số đối nhau)
Từ 3 ví dụ trên, ta nhận thấy tổng của hai số nguyên khác dấu có thể là số âm, có thể là số dương, có thể là 0.
Do vậy không thể kết luận chính xác được là số dương hay số âm.
Hoạt động 5 trang 64 Toán lớp 6 Tập 1: Tính và so sánh giá của a + b và b + a với a = - 7, b = 11.
Lời giải:
Ta có:
a + b = -7 + 11 = 11 – 7 = 4 (do 11 > 7)
b + a = 11 + (-7) = 11 – 7 = 4 (do 11 > 7)
Vì 4 = 4 nên a + b = b + a
Vậy a + b = b + a.
Lời giải:
(a + b) + c = [2 + (-4)] + (-6)
= - (4 - 2) + (-6) (do 4 > 2)
= - 2 + (-6)
= - (2 + 6)
= - 8
a + (b + c) = 2 + [(-4) + (-6)]
= 2 + [-(4 +6)]
= 2 + (-10)
= - (10 - 2) (do 10 > 2)
= - 8
Vì - 8 = - 8 nên (a + b) + c = a + (b + c)
Vậy (a + b) + c = a + (b + c).
Luyện tập 4 trang 65 Toán lớp 6 Tập 1: Tính một cách hợp lí:
a) (-2019) + (-550) + (-451)
b) (-2) + 5 + (-6) + 9
Lời giải:
a) (-2 019) + (-550) + (-451) = [(-2 019) + (-451)] + (-550) (tính chất giao hoán và kết hợp)
= - (2 019 + 451) + (-550)
= (- 2 470) + (- 550)
= - (2 470 + 550)
= - 3 020
b) (-2) + 5 + (-6) + 9
= [(-2) + (-6)] + (5 + 9) (tính chất giao hoán và kết hợp)
= - (2 + 6) +14 = (-8) + 14 = 14 – 8 = 6 (do 14 > 8).
Giải bài toán trên bằng hai cách:
Cách 1. Tính hiệu giữa số tiền lãi và số tiền lỗ.
Cách 2. Hiểu lỗ 2 triệu là “lãi” – 2 triệu để quy về tính tổng của hai số nguyên.
Lời giải:
Cách 1. Hiệu giữa số tiền lãi và số tiền lỗ là: 5 - 2 = 3 (triệu đồng)
Vậy tháng đó cửa hàng đó lãi 3 triệu đồng.
Cách 2. Lỗ 2 triệu đồng nghĩa là lãi (-2) triệu đồng
Cửa hàng đó lãi: 5 + (-2) = 3 (triệu đồng)
Vậy tháng đó cửa hàng đó lãi 3 triệu đồng.
Hoạt động 8 trang 65 Toán lớp 6 Tập 1: Hãy quan sát ba dòng đầu và dự đoán kết quả ở hai dòng cuối:
3 - 1 = 3 + (-1)
3 - 2 = 3 + (-2)
3 - 3 = 3 + (-3)
3 - 4 = ?
3 - 5 = ?
Lời giải:
Dự đoán: 3 – 4 = 3 +(-4)
3 – 5 = 3 + (-5)
Luyện tập 5 trang 66 Toán lớp 6 Tập 1: Tính các hiệu sau:
a) 5 – (-3)
b) (-7) - 8.
Lời giải:
a) 5 – (-3); = 5 + 3 = 8.
b) (-7) – 8 = (- 7) + (- 8) = - (7 + 8) = -15.
Lời giải:
Nhiệt độ bên ngoài của máy bay ở độ cao 10 000m và khi hạ cánh chênh lệch nhau:
27 - (- 48) = 27 + 48 = 75 (oC)
Vậy nhiệt độ bên ngoài của máy bay ở độ cao 10 000m và khi hạ cánh chênh lệch nhau 75 oC.
Bài tập
Bài 3.9 trang 66 Toán lớp 6 Tập 1: Tính tổng hai số cùng dấu:
a)(-7) + (-2);
b)(-8) + (-5);
c)(-11) + (-7);
d)(-6) + (-15).
Lời giải:
a) (-7) + (-2)
= - (7 + 2)
= - 9
b) (-8) + (-5)
= - (8 + 5)
= - 13
c) (-11) + (-7)
= - (11 + 7)
= - 18
d) (-6) + (-15).
= - (6 + 15)
= - 21.
Bài 3.10 trang 66 Toán lớp 6 Tập 1: Tính tổng hai số khác dấu
a) 6 + (-2);
b) 9 + (-3);
c) (-10) + 4;
d) (-1) + 8.
Lời giải:
a) 6 + (-2)
= 6 – 2 (do 6 > 2)
= 4
b) 9 + (-3)
= 9 – 3 (do 9 > 3)
= 6
c) (-10) + 4
= - (10 - 4) (do 10 > 4)
= - 6
d) (-1) + 8
= 8 – 1 (do 8 > 1)
= 7
Bài 3.11 trang 66 Toán lớp 6 Tập 1: Biểu diễn – 4 và số đối của nó trên cùng một trục số.
Lời giải:
Số đối của -4 là 4. Ta biểu diễn chúng trên trục số:
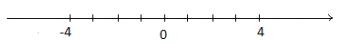
Bài 3.12 trang 66 Toán lớp 6 Tập 1: Thực hiện các phép trừ sau:
a) 9 – (-2)
b) (-7) – 4;
c) 27 – 30;
d) (-63) – ( -15).
Lời giải:
a) 9 – (-2);
= 9 + 2
= 11
b) ) (-7) – 4
= (-7) + (-4)
= - (7 + 4)
= -11
c) 27 – 30;
= 27 + (- 30)
= - (30 – 27) (do 30 > 27)
= - 3
d) (-63) – ( -15)
= (- 63) + 15
= - (63 – 15) (do 63 > 15)
= - 48
a) 11 km/h và 6 km/h?
b) 11 km/h và – 6 km/h?

Lời giải:
Sau 1 giờ, ca nô có vận tốc 11km/h đi được quãng đường:
11.1 = 11 (km)
Sau 1 giờ, ca nô có vận tốc 6km/h đi được quãng đường:
6.1 = 6 (km)
a) Vì vận tốc của hai ca nô đều dương nên hai ca nô cùng đi về phía B (chiều từ C đến B là dương) nên khoảng cách sau 1 giờ của hai ca nô sẽ là hiệu quãng đường đi được của chúng.
Sau 1 giờ, hiệu quãng đường đi của chúng là:
11 – 6 = 5 (km)
Vậy sau 1 giờ, hiệu quãng đường đi của chúng là 5km.
b) Ca nô có vận tốc 11km/h (là vận tốc dương) nên có chiều đi từ C đến B. Ca nô có vận tốc -6km/h (là vận tốc âm) nên có chiều đi từ C đến A.
Do đó hai ca nô đi ngược chiều nhau, nên khoảng cách sau 1 giờ của hai ca nô sẽ là tổng quãng đường đi được của chúng.
Sau 1 giờ hai ca nô cách nhau:
11 + 6 = 17 (km)
Vậy sau 1 giờ hai ca nô cách nhau 17km.
Bài 3.14 trang 66 Toán lớp 6 Tập 1: Mỗi hình sau đây mô phỏng phép tính nào?
a) 
b) 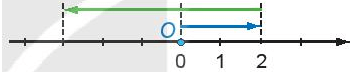
Lời giải:
a) Hình mô phỏng phép tính: (-5) + 3 hoặc (-5) - (- 3);
b) Hình mô phỏng phép tính: 2 – 5 hoặc 2 + (-5).
Bài 3.15 trang 66 Toán lớp 6 Tập 1: Tính nhẩm:
a) (-3) + (-2);
b) (-8) – 7;
c) (-35) + (-15);
d) 12 – (-8).
Lời giải:
a) (-3) + (-2)
= - (3 + 2)
= -5
b) (-8) – 7
= (-8) + (-7)
= - (8 + 7)
= - 15
c) (-35) + (-15)
= - (35 + 15)
= - 50
d) 12 – (-8
= 12 + 8
= 20.
Bài 3.16 trang 66 Toán lớp 6 Tập 1: Tính một cách hợp lí:
a) 152 + (-73) – (-18) - 127
b) 7 + 8 + (-9) + (-10).
Lời giải:
a) 152 + (-73) – (-18) - 127
= [152 - (-18)] - [127 - (-73)]
= (152 + 18) – (127 + 73)
= 170 - 200
= - 30
b) 7 + 8 + (-9) + (-10).
= [(7 + (-9)] + [8 + (-10)]
= (- (9 – 7)] + [- (10 – 8)]
= (-2) + (-2)
= - (2 + 2)
= - 4.
Bài 3.17 trang 66 Toán lớp 6 Tập 1: Tính giá trị của biểu thức (-156) - x, khi:
a) x = -26;
b) x = 76;
c) x = (- 28) – (- 143).
Lời giải:
a) Thay x = -26 vào biểu thức (-156) - x ta được:
(-156) – x = (-156) – (-26) = (-156) + 26 = - (156 – 26) = - 130. (do 156 > 26)
b) Thay x = 76 vào biểu thức (-156) - x ta được:
(-156) – x = (-156) – 76 = (-156) + (-76) = - (156 + 76) = - 232.
c) Thay x = (- 28) – (- 143) vào biểu thức (-156) - x ta được:
(-156) – x = (-156) – [(-28) – (-143)] = (-156) – [(-28) + 143] = (-156) – (143 – 28)
= (- 156) – 115 = (-156) + (-115) = - (156 + 115) = - 271.
Bài 3.18 trang 66 Toán lớp 6 Tập 1: Thay mỗi dấu “*” bằng một chữ số thích hợp để có:
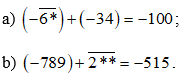
Lời giải:
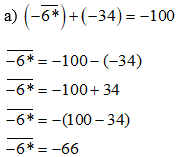
Vậy dấu * là chữ số 6.
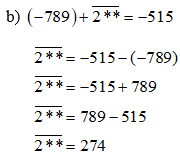
Vậy hai dấu * lần lượt theo thứ tự từ trái qua phải là 7 và 4.
Lý thuyết Phép cộng và phép trừ số nguyên
1. Cộng hai số nguyên cùng dấu
Quy tắc cộng hai số nguyên âm
Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “-“ trước kết quả.
Ví dụ 1. Tính:
a) (-23) + (-55); b) 43 + 23; c) (-234) + (-546).
Lời giải
a) (-23) + (-55) = - (23 + 55) = - 78;
b) 43 + 23 = 66;
c) (-234) + (-546) = - (234 + 546) = - 780.
2. Cộng hai số nguyên khác dấu
Hai số đối nhau:
Hai số nguyên a và b được gọi là đối nhau nếu a và b nằm khác phía với điểm 0 và có cùng khoảng cách đến gốc 0.
Chú ý:
Ta quy ước số đối của 0 là chính nó.
Tổng của hai số đối nhau luôn bằng 0.
Ví dụ 2. Tìm số đối của -3; 4; -5; 8; -12.
Lời giải
Số đối của – 3 là 3;
Số đối của 4 là -4;
Số đối của – 5 là 5;
Số đối của 8 là – 8;
Số đối của -12 là 12.
Quy tắc cộng hai số nguyên khác dấu:
+ Hai số nguyên đối nhau thì có tổng bằng 0.
+ Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phân số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.
Ví dụ 3. Thực hiện các phép tính:
a) 312 + (-134); b) (– 254) + 128; c) 2 304 + (-115).
Lời giải
a) 312 + (-134) = 312 – 134 = 178;
b) (– 254) + 128 = - ( 254 – 128) = -128;
c) 2 304 + (-115) = 2 304 – 115 = 2 189.
3. Tính chất của phép cộng
Phép cộng số nguyên có tính chất sau:
+ Giao hoán: a + b = b + a;
+ Kết hợp: (a + b) + c = a + (b + c).
Ví dụ 4. Tính một cách hợp lí:
a) (-350) + (-296) + 50 + 96;
b) (-3) + 5 + (-7) + 5.
Lời giải
a) (-350) + (-296) + 50 + 96
= [(-350) + 50] + [(-296) + 96]
= (-300) + (-200)
= -500.
b) (-3) + 5 + (-7) + 5
= [(-3) + (-7)] + [5 + 5]
= (-10) + 10
= 0.
4. Trừ hai số nguyên
Quy tắc trừ hai số nguyên
Muốn trừ số nguyên a cho số nguyên b, ta cộng số nguyên a với số đối của số nguyên b:
a – b = a + (-b).
Ví dụ 5. Tính:
a) 15 – 7; b) 8 – 9; c) 23 – 154; d) 12 – 125 – 83.
Lời giải
a) 15 – 7 = 8;
b) 8 – 9 = 8 + (-9) = - (9 – 8) = -1;
c) 23 – 154 = - ( 154 – 23) = -131;
d) 12 – 125 – 83
= 12 + (-125) + (-83)
= -(125 – 12) + (-83)
= (-113) + (-83)
= -(113 + 83)
= - 196.
Bài giảng Toán 6 Bài 14: Phép cộng và phép trừ số nguyên - Kết nối tri thức
Xem thêm các bài giải SGK Toán lớp 6 Kết nối tri thức hay, chi tiết khác: