Viết phương trình mặt cầu (S) có đường kính AB với
A.
B.
C.
D. Đáp án khác
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Phương pháp giải:
B1: Tính độ dài đường kính => độ dài bán kính
B2: Tìm tọa độ tâm (là trung điểm của đường kính)
B3: Đưa vào phương trình tổng quát
Mặt cầu có phương trình dạng có tâm và bán kính .
Lời giải:
Ta có:
![]()
Gọi I là trung điểm AB nên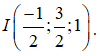
Mặt cầu tâm 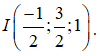 và bán kính
và bán kính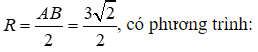
Viết phương trình mặt cầu
Phương pháp chung:
Cách 1: Sử dụng phương trình mặt cầu dạng tổng quát.
- Tìm tâm và bán kính mặt cầu, từ đó viết phương trình theo dạng:
- Mặt cầu có phương trình dạng có tâm và bán kính .
Cách 2: Sử dụng phương trình mặt cầu dạng khai triển.
- Gọi mặt cầu có phương trình
- Sử dụng điều kiện bài cho để tìm .
Tham khảo thêm một số tài liệu liên quan:
Phương trình mặt cầu: lý thuyết, các dạng bài tập và phương pháp giải
Trắc nghiệm Ôn thi THPT QG Toán 12: Đáp án hình học không gian mức độ thông hiểu
Trong không gian Oxyz, cho ba điểm Giá trị của x, y để ba điểm A; B; C thẳng hàng là
Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng lần lượt có phương trình . Phương trình mặt phẳng (P) cách đều hai đường thẳng d1;d2 là:
Trong không gian Oxyz, cho mặt phẳng và đường thẳng . Trong các mệnh đề sau, mệnh đề nào đúng?
Cho đường thẳng và mặt phẳng Góc giữa đường thẳng ∆ và mặt phẳng (P) là:
Cho đường thẳng và điểm Đường thẳng d cắt mặt cầu (S) có tâm I, tại hai điểm A, B sao cho Phương trình của mặt cầu (S) là:
Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng và (S) tiếp xúc với hai mặt phẳng
Trong không gian tọa độ Oxyz, cho ba điểm Để tứ giác ABCD là hình bình hành thì tọa độ điểm D là
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;-2;1); B(-1;3;3); C(2;-4;2). Một vectơ pháp tuyến 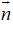
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng:
Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β).
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng và tiếp xúc với mặt cầu