Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với đường tròn (A, B là hai tiếp điểm). Lấy điểm C trên cung nhỏ AB (C không trùng với A, B). Từ điểm C kẻ CD vuông góc với AB, CE vuông góc với MA, CF vuông góc với MB (). Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng
a) Tứ giác ADCE nội tiếp đường tròn.
b) Hai tam giác CDE và CFD đồng dạng
c) Tia đối của tia CD là tia phân giác của góc
d) Đường thẳng IK song song với đường thẳng AB.
 Giải bởi Vietjack
Giải bởi Vietjack
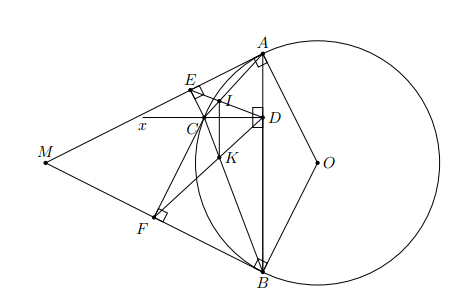
a) Tứ giác ADCE có nên ADCE là tứ giác nội tiếp.
b) Tứ giác ADCE nội tiếp nên
Tương tự, tứ giác BDCF nội tiếp, suy ra
Mặt khác, theo tính chất của góc tạo bởi tiếp tuyến và dây cung thì
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ và cung nhỏ . Hai dây AN và CM cắt nhau tại I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
a) Chứng minh các điểm C, N, K, I cùng thuộc một đường tròn.
b) Chứng minh
c) Chứng minh tứ giác BHIK là hình thoi.
d) Gọi PQ lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.
Cho đường tròn tâm O, đường kính AB cố định. H là điểm cố định thuộc đoạn OA (H không trùng O và A). Qua H vẽ đường thẳng vuông góc với AB cắt đường tròn tâm O tại C và D. Gọi K là điểm tùy ý thuộc cung lớn CD (K không trùng các điểm C, D và B). Gọi I là giao điểm của AK và CD.
a) Chứng minh tứ giác HIKB nội tiếp đường tròn.
b) Chứng minh AI.AK = AH.AB
c) Chứng minh khi điểm K thay đổi trên cung lớn CD của đường tròn tâm O thì tâm đường tròn ngoại tiếp tam giác KCI luôn thuộc một đường thẳng cố định.
Cho đường tròn (O) ngoại tiếp tam giác nhòn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
a) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.
b) Chứng minh = NK.NM
c) Chứng minh tứ giác BHIK là hình thoi.
d) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.
Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Tiếp tuyến của đường tròn tâm O tại điểm C cắt các đường thẳng AB và AD theo thứ tự tại M, N. Dựng AH vuông góc với BD tại điểm H; K là giao điểm của hai đường thẳng MN và BD.
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.
b) Chứng minh rằng: AD.AN = AB.AM
c) Gọi E là trung điểm của MN. Chứng minh ba điểm A, H, E thẳng hàng.
d) Cho AB = 6 cm, AD = 8 cm. Tính độ dài đoạn MN.
Tam giác AMB cân tại M nội tiếp trong đường tròn (O; R). Kẻ MH vuông góc AB () ,MH cắt đường tròn tại N. Biết MA = 10 cm, AB = 12 cm.
a) Tính MH và bán kính R của đường tròn.
b) Trên tia đối tia BA lấy điểm C. Tia MC cắt đường tròn tại D, ND cắt AB tại E. Chứng minh tứ giác MDEH nội tiếp và chứng minh các hệ thức sau: và
c) Chứng minh NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE.
Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (D, E thuộc đường tròn (O); D nằm giữa A và E, tia AD nằm giữa hai tia AB, AO).
a) Chứng minh rằng A, B, O, C cùng thuộc một đường tròn và xác định tâm của đường tròn này.
b) Chứng minh rằng
c) Gọi H là giao điểm của OA và BC. Chứng minh rằng và tứ giác DEOH nội tiếp.
d) Đường thẳng AO cắt đường tròn (O) tại M, N (M nằm giữa A và O). Chứng minh rằng
Cho tam giác ABC có ba góc nhọn (AB < AC), dựng AH vuông góc với BC tại điểm H. Gọi M, N theo thứ tự là hình chiếu vông góc của điểm H trên AB và AC. Đường thẳng MN cắt đường thẳng BC tại điểm D. Trên nửa mặt phẳng bờ CD chứa điểm A, vẽ nửa dường tròn đường kính CD. Qua B kẻ đường thẳng vuông góc với CD cắt nửa đường tròn trên tại E.
a) Chứng minh rằng tứ giác AMHN là tứ giác nội tiếp.
b) Chứng minh
c) Chứng minh rằng
d) Gọi O là tâm đường tròn ngoại tiếp tam giác MNE. Chứng minh rằng
Cho tam giác nhọn ABC có AB < AC và đường cao AK. Vẽ đường tròn tâm O đường kính BC. Từ A kẻ các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm; M và B nằm trên nửa mặt phẳng có bờ là đường thẳng AO). Gọi H là giao điểm của hai đường thẳng MN và AK. Chứng minh rằng:
a) Tứ giác AMKO nội tiếp đường tròn.
b) KA là tia phân giác của
c) = AK.AH
d) H là trực tâm của tam giác ABC.
Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Từ A kẻ hai tiếp tuyến AB và AC (B, C là các tiếp điểm).
a) Chứng minh tứ giác ABOC là tứ giác nội tiếp.
b) Gọi H là trực tâm tam giác ABC. Chứng minh tứ giác BOCH là hình thoi.
c) Gọi I là giao điểm của đoạn OA với đường tròn (O). Chứng minh I là tâm đường tròn nội tiếp tam giác ABC.
d) Cho OB = 3cm, OA = 5cm. Tính diện tích tam giác ABC.
Cho tam giác ABC nội tiếp đường tròn (O; R). Gọi đường tròn (I; r) đường tròn nội tiếp tam giác ABC, H là tiếp điểm của AB với đường tròn (I), D là giao điểm của AI với đường tròn (O), DK là đường kính của đường tròn (O). Gọi d là độ dài của OI. Chứng minh rằng:
a)
b)
c)
d)
Cho điểm C thuộc nửa đường tròn đường kính AB. Kẻ tiếp tuyến Ax của nửa đường tròn đó (Ax nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng AB chứa nửa đường tròn). Tia phân giác của góc Cax cắt nửa đường tròn tại D. kéo dài AD và BC cắt nhau tại E. kẻ EH vuông góc với Ax tại H.
a) Chứng minh tứ giác AHEC nội tiếp đường tròn.
b) Chứng minh
c) Chứng minh tam giác ABE cân.
d) Tia BD cắt AC và Ax lần lượt tại F và K. Chứng minh AKEF là hình thoi.
Cho đường tròn tâm O, đường kính AB = 2R. Lấy với AM < BM. Trên cạnh MB lấy điểm C sao cho MC = MA. Gọi OD là bán kính vuông góc với AB (M và D ở hai bên đường thẳng AB)
a) Chứng minh . Tính theo R độ dài các cạnh của
b) Chứng tỏ MD là phân giác và
c) Chứng minh rằng D là tâm của đường tròn (ABC)
d) Đường tròn (ABC) cắt MD tại I. Chứng minh I là tâm đường tròn nội tiếp
Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt các đoạn BC và OC lần lượt tại D và I. Gọi H là hình chiếu vuông góc của A lên OC, AH cắt BC tại M.
a) Chứng minh tứ giác ACDH là nội tiếp và
b) Chứng minh hai tam giác OHB và OBC đồng dạng với nhau và HM là tia phân giác của góc
c) Gọi K là trung điểm của BD chứng minh MD.BC = MB.CD và MB.MD = MK.MC.
d) Gọi E là giao điểm của AM và OK, J là giao điểm của IM và (O) (J khác I). Chứng minh hai đường thẳng OC và EJ cắt nhau tại một điểm trên (O).
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (C) tâm o bán kính R. Hai đường cao AE và BK của tam giác ABC cắt nhau tại H (với E thuộc BC, K thuộc AC)
a) Chứng minh tứ giác ABEK nội tiếp được trong một đường tròn.
b) Chứng minh CE.CB = CK.CA
c) Chứng minh
d) Cho B, C cố định và A di động trên ( C) nhưng vẫn thỏa mãn điều kiện tam giác ABC nhọn, khi đó H thuộc một đường tròn (T) cố định. Xác định tâm I và tính bán kính r của đường tròn (T), biết R = 3 cm.