Trong mặt phẳng tọa độ Oxy, cho điểm M(–2; 4). Phép vị tự tâm O tỉ số k = –2 biến điểm M thành điểm nào trong các điểm sau?

A. (–3; 4).

B. (–4; –8).

C. (4; –8).

D. (4; 8).

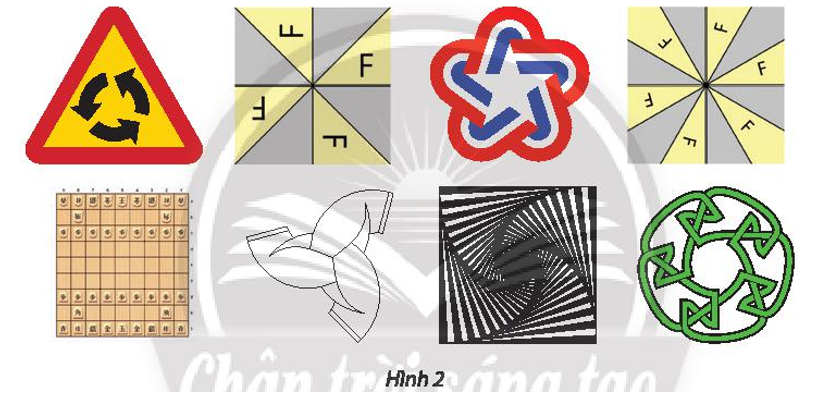
Gọi O được gọi là tâm đối xứng quay bậc n (n ∈ ℕ*) của hình ℋ nếu sau khi thực hiện phép quay $Q_{\left(O,\frac{360°}{n}\right)}$ ta lại được chính hình ℋ. Hình có tâm đối xứng quay bậc n gọi là hình đối xứng quay bậc n. Tìm các hình đối xứng quay trong Hình 2.

$\frac{360°}{n}=120°$

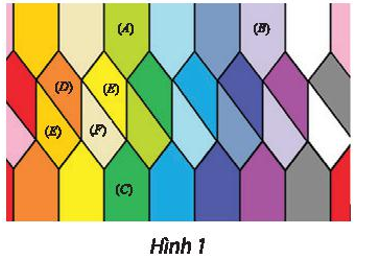
Cho Hình 1.

a) Tìm phép biến hình f biến hình (A) thành hình (B).

b) Tìm phép biến hình g biến hình (A) thành hình (C).

c) Tìm các phép biến hình biến hình (D) thành lần lượt các hình (E), (F), (G).

Cho đường thẳng d: x + y + 2 = 0, đường tròn (C): x² + y² – 4x + 8y – 5 = 0.

a) Tìm ảnh của d qua phép đối xứng trục Ox.

b) Tìm ảnh của (C) qua phép đối xứng trục Oy.

Cho đường tròn (O; R) và điểm I cố định khác O. Vẽ điểm M tùy ý trên (O). Tia phân giác của góc MOI cắt IM tại N. Điểm N di động trên đường nào khi M di động trên (O)?

Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 5). Phép tịnh tiến theo vectơ $\overrightarrow{v}=\left(1;2\right)$ biến điểm M thành điểm có tọa độ là

A. (3; 1).

B. (1; 6).

C. (3; 7).

D. (4; 7).

Trong mặt phẳng tọa độ Oxy, cho M(3; 2), N(2; 0).

a) Tìm ảnh của các điểm M, N qua phép vị tự tâm I(–1; –1) tỉ số k = –2.

b) Tìm ảnh của các điểm M, N qua phép vị tự tâm O tỉ số k = 3.

Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình ℋ. Hỏi ℋ có mấy trục đối xứng?

A. 0.

B. 1.

C. 2.

D. 3.

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + 6y – 5 = 0.

a) Tìm ảnh của đường thẳng d qua phép đối xứng tâm O.

b) Tìm ảnh của đường thẳng d qua phép đối xứng tâm M(4; 6).

Cho tam giác ABC có góc B, góc C đều là góc nhọn. Nêu cách vẽ hình chữ nhật DEFG có đỉnh D, đỉnh E thuộc cạnh BC, đỉnh F, đỉnh G thuộc cạnh AC, AB và có EF = 2DE.

Cho tam giác ABC. Vẽ về phía ngoài của tam giác các hình vuông ABEF, ACMN. Chứng minh BN bằng và vuông góc với FC.

Cho điểm A chạy trên nửa đường tròn đường kính BC cố định. Vẽ về phía ngoài tam giác ABC hình vuông ABEF. Chứng minh rằng điểm E chạy trên một nửa đường tròn cố định.

Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O với góc quay 45°?

A. M’(1; 1).

B. M’(1; 0).

C. $M^{\text{'}}\left(\sqrt{2};0\right)$.

D. $M^{\text{'}}\left(0;\sqrt{2}\right)$.

Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O với góc quay α, 0 < α ≤ 2π, biến tam giác trên thành chính nó?

A. Một.

B. Hai.

C. Ba.

D. Bốn.

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x = 2. Trong các đường thẳng sau đường thẳng nào là ảnh của d qua phép đối xứng tâm O?

A. x = 2.

B. y = 2.

C. x = –2.

D. y = –2.