Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;7), . Gọi (S') là mặt cầu tâm I đi qua hai điểm A, B sao cho OI nhỏ nhất. M(a,b,c) là điểm thuộc (S'), giá trị lớn nhất của biểu thức T=2a-b+2c là
A. 18
B. 7
C. 156
D. 6
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Tâm I mặt cầu (S') đi qua hai điểm A, B nằm trên mặt phẳng trung trực của . Phương trình mặt phẳng trung trực của AB là (P): x+2y+3z-14=0.
OInhỏ nhất khi và chỉ khi I là hình chiếu vuông góc của O trên mặt phẳng (P).
Đường thẳng d qua O và vuông góc với mặt phẳng (P) có phương trình .
Tọa độ điểm I khi đó ứng với t là nghiệm phương trình
.
Bán kính mặt cầu (S') là R=IA=4.
Từ T = 2a-b+2c => 2a-b+2c-T, suy ra M thuộc mặt phẳng (Q): 2x-y+2z-T=0.
Vì M thuộc mặt cầu nên:
.
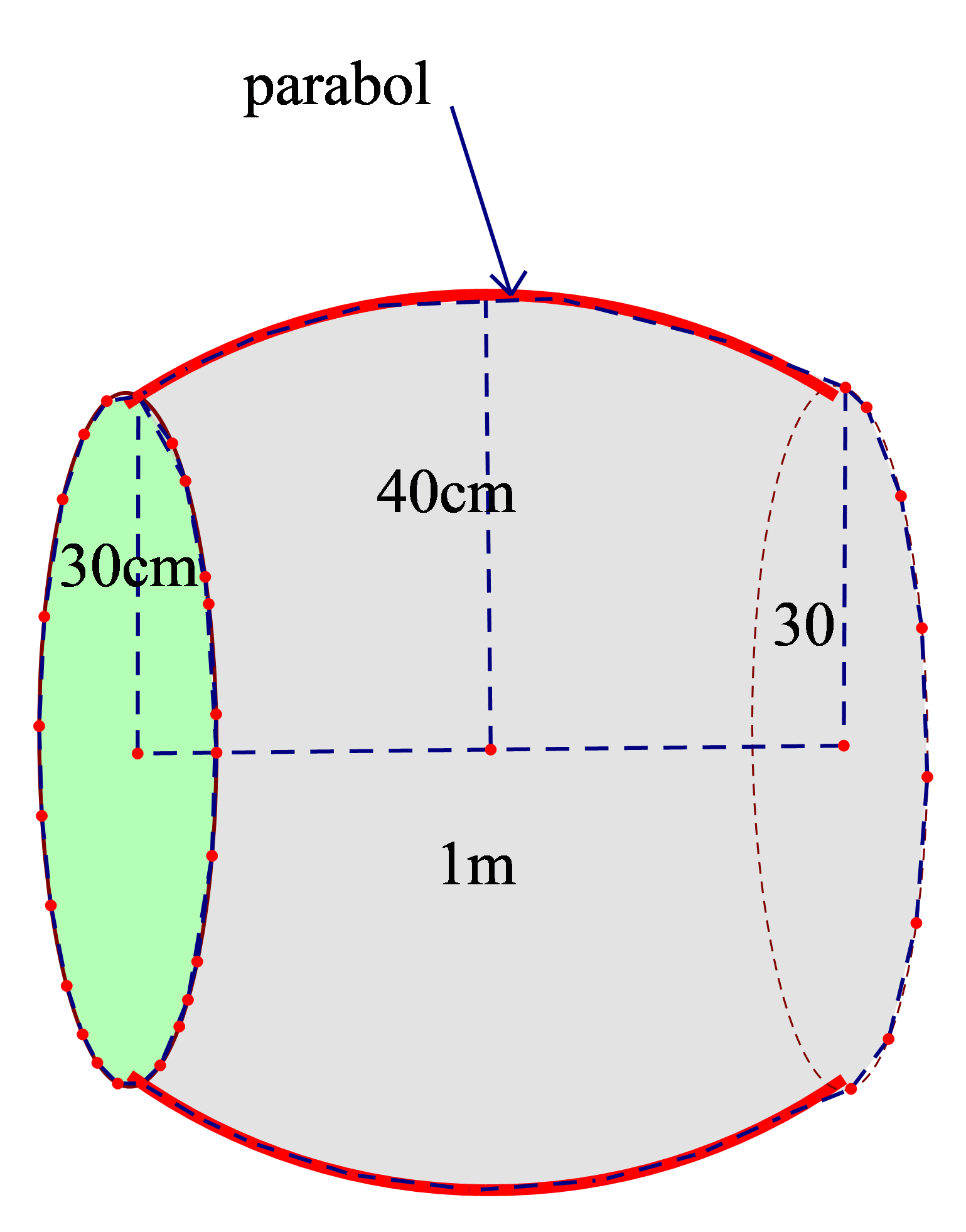
Một cái trống trường có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách đều hai đáy có diện tích là , chiều dài của trống là 1m. Biết rằng mặt phẳng chứa trục cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu?
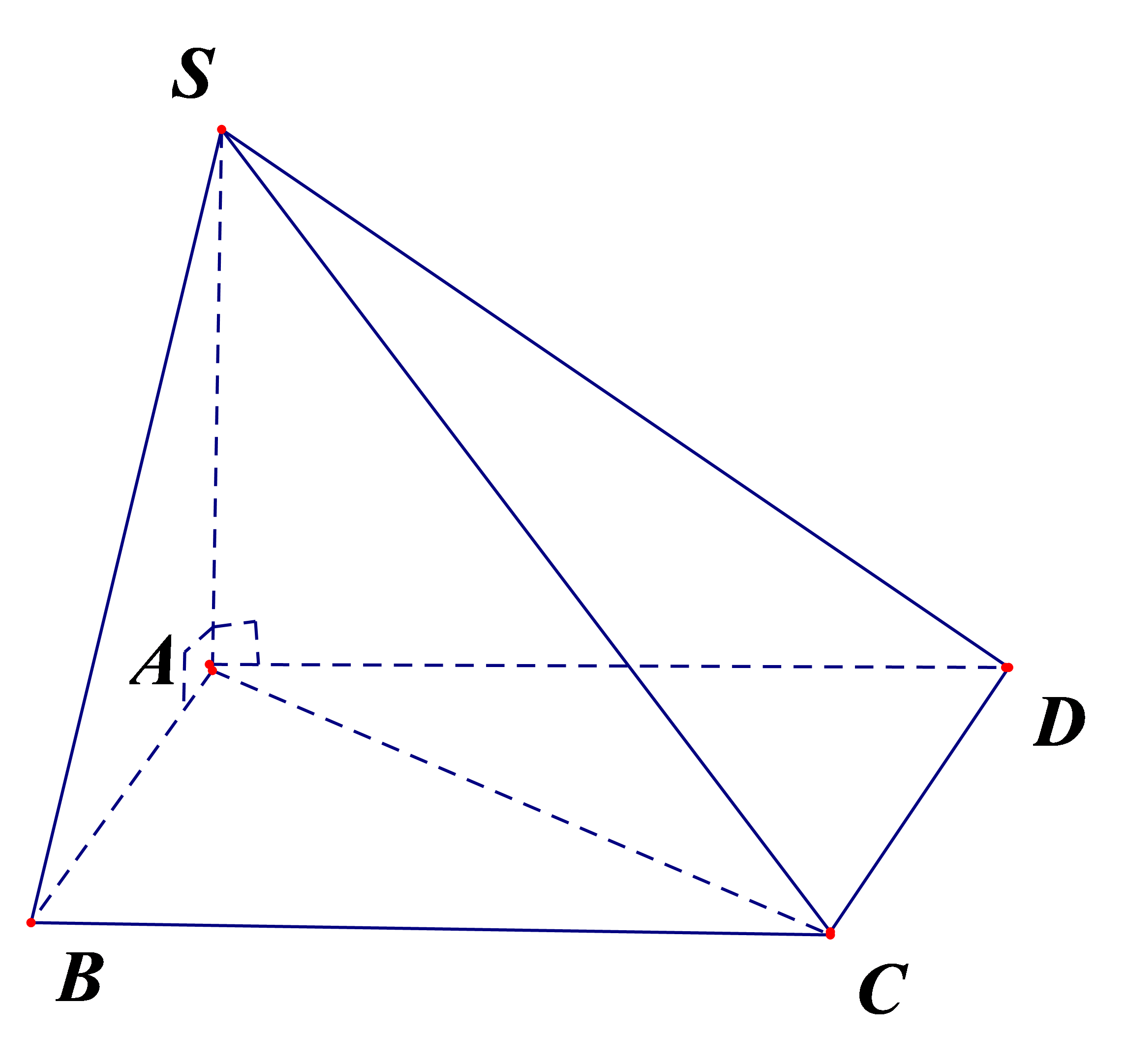
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a có SA vuông góc với mặt phẳng (ABCD) và SA=2a. Khi đó góc giữa SB và (SAC) bằng:
Cho hàm số f(x) có bảng biến thiên như hình sau:
Hàm số có bao nhiêu điểm cực đại?
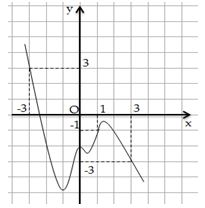
Cho hàm số y = f(x) có đạo hàm liên tục trên R, hàm số có đồ thị như hình vẽ dưới đây.
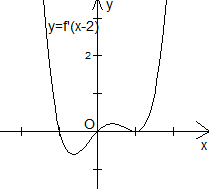
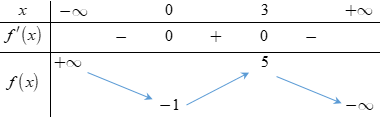
Cho hàm số có bảng biến thiên như hình vẽ:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?