 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là B
Mặt cầu có tâm I (–1; 2; –3) nên phương trình mặt cầu có dạng là:
(x + 1)2 + (y – 2)2 + (z + 3)2 = R2 (1)
Vì mặt cầu đi qua điểm A (2; 0; 0) nên thay tọa độ điểm A vào (1) ta được:
(2 + 1)2 + (0 – 2)2 + (0 + 3)2 = R2 => R2 = 22
Vậy phương trình mặt cầu là: (x + 1)2 + (y – 2)2 + (z + 3)2 = 22.
Viết phương trình mặt cầu khi biết tâm và bán kính
Phương pháp giải:
Bước 1: Xác định tâm I (a; b; c).
Bước 2: Xác định bán kính R của (S).
Bước 3: Thế vào phương trình (S):
Dạng phương trình mặt cầu (S) có tâm I (a; b; c) và bán kính R.
(S): (x - a)2 + (y - b)2 + (z - c)2 = R2
Bài tập liên quan:
Phương trình mặt cầu có tâm và tiếp xúc với trục Oy là:
A.
B.
C.
D.
Cách giải:
Chọn C
Phương pháp giải:
Mặt cầu tâm có bán kính R thì có phương trình là
Giải chi tiết:
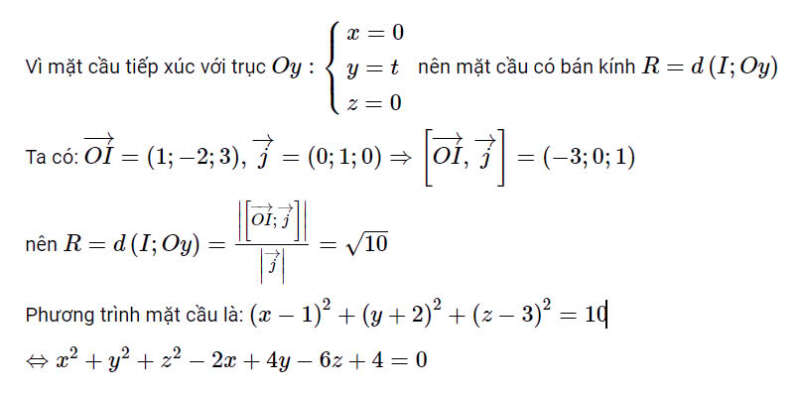
Tham khảo thêm một số tài liệu liên quan:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình x – 3z + 5 = 0. Hãy tìm tọa độ một vectơ pháp tuyến của (P)