Trong các câu sau đây, câu nào sai?
A. Hai tam giác có cặp cạnh tương ứng bằng nhau và cặp góc xen giữa hai cặp cạnh đó bằng nhau thì hai tam giác bằng nhau.
B. Hai tam giác có một cặp cạnh tương ứng bằng nhau và hai cặp góc tương ứng cùng kề với cặp cạnh đó bằng nhau thì hai tam giác bằng nhau.
C. Hai tam giác bằng nhau có các cặp cạnh tương ứng bằng nhau và các cặp góc tương ứng bằng nhau.
D. Hai tam giác có các cặp góc tương ứng bằng nhau thì các cặp cạnh tương ứng bằng nhau.
Giải bởi Vietjack
Đáp án đúng là: D
Câu A đúng theo trường hợp bằng nhau cạnh – góc – cạnh của hai tam giác.
Câu B đúng theo trường hợp bằng nhau góc – cạnh – góc của hai tam giác.
Câu C đúng theo định nghĩa hai tam giác bằng nhau.
Câu D sai, do hai tam giác chưa chắc đã bằng nhau.
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Chứng minh rằng MP = MQ và AP = AQ.
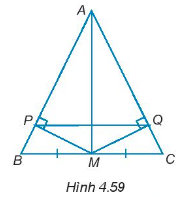
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Đường thẳng PQ có vuông góc với AM không? Vì sao?
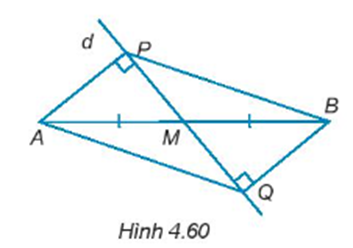
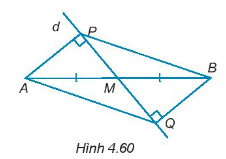
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
∆APB = ∆BQA.
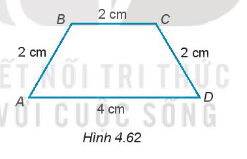
Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.
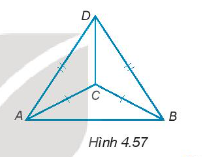
Cho các điểm A, B, C, D như Hình 4.57.
Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?
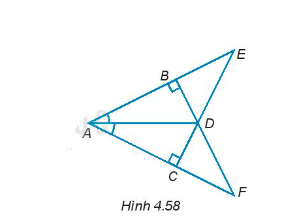
Cho các điểm A, B, C, D, E, F như Hình 4.58.
Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
AP = BQ.
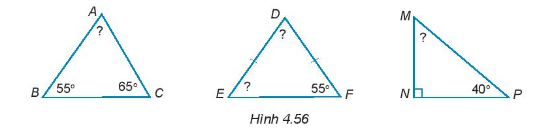
Tính số đo các góc chưa biết của các tam giác dưới đây (H.4.56).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
